ベクトルの線積分と周回積分
ベクトル場 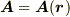 の中に,任意の曲線
の中に,任意の曲線 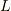 を描き,その端点を
を描き,その端点を 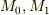 とし,その位置ベクトルを
とし,その位置ベクトルを 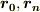 とします.そして,
とします.そして, 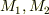 間の曲線を
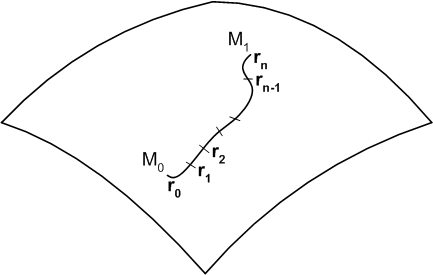
間の曲線を 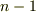 個の小部分に分割し,各点の位置ベクトルを
個の小部分に分割し,各点の位置ベクトルを 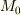 側から順に
側から順に 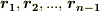 とします.
とします.
各点で定義されるベクトル場を 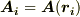 とし,次のような量の総和を考えてみます.ここで
とし,次のような量の総和を考えてみます.ここで 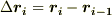 と置きます.
と置きます.

式 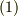 の右辺で
の右辺で 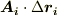 が内積であることに注意して下さい.今は
が内積であることに注意して下さい.今は 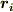 は有限個のベクトルで,曲線を
は有限個のベクトルで,曲線を  個の線分で近似する表現に過ぎませんが,次のように極限を取ることで,『ベクトル場
個の線分で近似する表現に過ぎませんが,次のように極限を取ることで,『ベクトル場 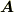 を曲線
を曲線 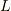 に射影した大きさの総和』を考えることが出来ます.
に射影した大きさの総和』を考えることが出来ます.
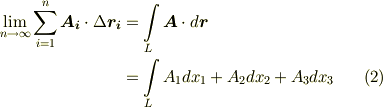
これを ベクトル場Aの,曲線Lに沿った線積分 と呼びます.また,とくに曲線が閉曲線の場合 Lに沿っての周回積分 と呼び,次のように積分記号に○を加えた記号で表わします.

このようにベクトル場の周回積分を取った値を, 循環 と呼びます.
線積分の物理的意味
式  を力学の問題で考えてみましょう.ベクトル場
を力学の問題で考えてみましょう.ベクトル場 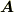 を質点にかかる力
を質点にかかる力 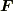 だとすると,式
だとすると,式 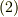 は,質点が曲線
は,質点が曲線 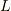 に沿って動くときに質点が受ける仕事
に沿って動くときに質点が受ける仕事 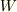 を表わします.
を表わします.
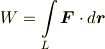
電磁気学では,電場 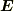 の中を,点電荷が曲線
の中を,点電荷が曲線 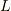 に沿って動くとき,電場から受ける仕事(電圧)がこの形で表わされます.
に沿って動くとき,電場から受ける仕事(電圧)がこの形で表わされます.
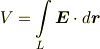
このように,線積分という計算が,ポテンシャルと呼ばれる量と関係深いことを記憶に留めておいてください.( スカラーポテンシャル で,再びこの話題に触れます.)また,飛行機の翼に働く揚力 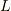 は,翼の周りの流れ
は,翼の周りの流れ 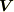 に関する循環
に関する循環 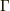 を使って表現されることが知られています.翼に当たる気流の速度を
を使って表現されることが知られています.翼に当たる気流の速度を 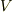 ,空気密度を
,空気密度を 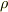 とします.
とします.
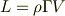
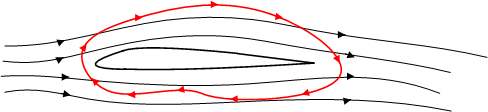
| [*] | この揚力の公式は,二次元翼(翼は無限に長いとする)に関する理論で,クッタ=ジュウコフスキーの定理と呼ばれるものです.この記事で詳しく説明することは出来ないので,興味のある人は,流体力学,航空力学,飛行力学などといった題名の本をあたって下さい. |
線積分になりたつ公式
積分という演算も線形ですから,曲線 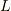 が幾つかの部分
が幾つかの部分 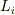 に分かれるとき,次の関係がなりたちます.
に分かれるとき,次の関係がなりたちます.
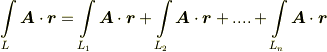
また,始点と終点を逆転すれば,積分の値も符号が変わります.(周回積分では回転方向を逆にすれば,符号が変わります.)
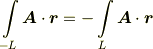
特に,周回積分に関して,閉曲線 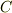 を二つの部分
を二つの部分 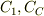 に分割すると,次の関係式がなりたちます.
に分割すると,次の関係式がなりたちます.
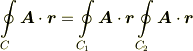
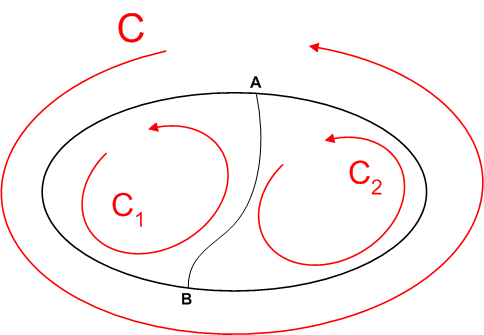
これは図を考えれば分かりやすいと思います.次図のように,閉曲線 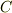 を途中に曲線
を途中に曲線 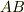 を引いて分割した場合,区間
を引いて分割した場合,区間 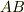 では
では 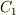 の周回積分と
の周回積分と 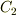 の周回積分の向きがちょうど逆になるため,互いに打ち消しあい,結局,元の
の周回積分の向きがちょうど逆になるため,互いに打ち消しあい,結局,元の 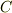 の周回積分しか残らないと考えれば良いのです.
の周回積分しか残らないと考えれば良いのです.
| [†] | 線積分で始点と終点を逆にしたり,周回積分の回る向きを逆にすると,一般には積分の値の符号が変わるということでした.高校で習った 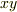 平面上の積分だって,向きを変えれば符号が変わりましたら,何も新しい話題ではないと思うかも知れません.しかし,敢えて何かが新しい感じがすると言えば,『曲線に沿って』とか,これから出てきますが『曲面に沿って』とか,図形と積分区間の関係が強まってきた感じがあります.ベクトル解析をこのまま進めていくと,この傾向はもっと強まり,本格的に図形の性質と積分が関係するようになってきます.こうなると,ベクトル解析というよりは微分幾何という分野に近くなってきますが,とても魅力的な分野です.線積分で『積分の向き(始点・終点)』として考えていたものが,面積分では『曲面の向き(表・裏)』に対応してきます.そして微分形式という理論では,こうした向きを 平面上の積分だって,向きを変えれば符号が変わりましたら,何も新しい話題ではないと思うかも知れません.しかし,敢えて何かが新しい感じがすると言えば,『曲線に沿って』とか,これから出てきますが『曲面に沿って』とか,図形と積分区間の関係が強まってきた感じがあります.ベクトル解析をこのまま進めていくと,この傾向はもっと強まり,本格的に図形の性質と積分が関係するようになってきます.こうなると,ベクトル解析というよりは微分幾何という分野に近くなってきますが,とても魅力的な分野です.線積分で『積分の向き(始点・終点)』として考えていたものが,面積分では『曲面の向き(表・裏)』に対応してきます.そして微分形式という理論では,こうした向きを 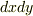 などの微小量の性質に織り込んで考えていくことになります.積分の向きも,なかなか大事ですよ. などの微小量の性質に織り込んで考えていくことになります.積分の向きも,なかなか大事ですよ. |