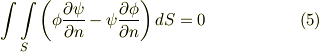ラプラス場
ベクトル場 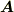 が,
が, 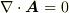 を満たすとき管状ベクトル場,
を満たすとき管状ベクトル場,  を満たすとき層状ベクトル場と呼ぶのでした.この両方を満たすようなベクトル場,すなわち管状でもあり層状でもあるベクトル場を ラプラス場 と呼びます.
を満たすとき層状ベクトル場と呼ぶのでした.この両方を満たすようなベクトル場,すなわち管状でもあり層状でもあるベクトル場を ラプラス場 と呼びます.
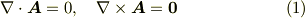
ラプラス場が単連結領域で定義されている場合,この流れは ラプラス方程式 を満たすスカラーポテンシャルによって記述されます.
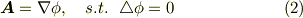
式 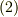 で表現される
で表現される 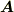 が,式
が,式 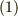 の条件を両方満たすことを確認してみて下さい.ラプラス方程式の解となる関数を,一般に 調和関数 と呼ぶのでした.調和関数には,以下に紹介するような重要な諸性質があります.ラプラス場の解析では,これらの性質が効いて来ます.
の条件を両方満たすことを確認してみて下さい.ラプラス方程式の解となる関数を,一般に 調和関数 と呼ぶのでした.調和関数には,以下に紹介するような重要な諸性質があります.ラプラス場の解析では,これらの性質が効いて来ます.
| [*] | 以下の諸性質は,ベクトル場の問題というよりは調和関数の性質に関する話題です.物理の様々な場面で,ラプラス方程式を適当な境界条件下で解く問題は重要ですが,これは,ベクトル解析の問題というよりは,微分方程式論もしくはポテンシャル論の守備範囲になると思います.ですから,これらの事項を今すぐ覚える必要はないと思いますが,いずれ使う日が来ると思いますので,ここでざっと見ておいても損はないと思います.この記事では,あまり詳しい所までは取り上げません. |
性質3
次の公式を グリーンの定理 の最後で求めました.
![\phi (M) = -\frac{1}{4\pi} \int \int \int \limits _{V} \frac{1}{r}\triangle \phi dV -\frac{1}{4\pi}\int \int \limits _{S} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} \frac{\partial }{\partial n} \right] dS \tag{6}](./ecc1f9ee7b4f87094923c8db4d01380e.png)
この右辺は  を代入すると第一項が消えて簡単化します.式
を代入すると第一項が消えて簡単化します.式 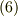 の表式に従う一般にはスカラーポテンシャル
の表式に従う一般にはスカラーポテンシャル  では,領域内の点
では,領域内の点 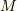 における値を決めるのに,領域における体積分と面積分の両方を考えなければならなかったのに対し,
における値を決めるのに,領域における体積分と面積分の両方を考えなければならなかったのに対し,  が調和関数なら,面積分だけで良くなるわけです.
が調和関数なら,面積分だけで良くなるわけです.
![\phi (M) = -\frac{1}{4\pi}\int \int \limits _{S} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} \frac{\partial }{\partial n} \right] dS \tag{7}](./68b497f50f789489113a096e48442f25.png)
また,式 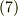 の曲面
の曲面 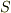 を点
を点 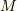 を中心とする半径
を中心とする半径  の球面
の球面  とすると,
とすると, 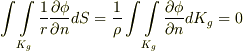 が成り立ちます.(球は全方位に対称ですから,法線ベクトルを全部足したら
が成り立ちます.(球は全方位に対称ですから,法線ベクトルを全部足したら 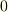 になりますね).また,
になりますね).また,  にも注意すると,式
にも注意すると,式 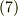 は次のように簡単化されます.
は次のように簡単化されます.

球対称なポテンシャルの分布を考える問題は,割合によく物理学に出て来る重要な形ですので,式 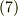 の形よりも式
の形よりも式 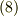 の簡単形で使う方が実用的かも知れません.式
の簡単形で使う方が実用的かも知れません.式 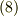 は『点
は『点 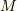 における調和関数
における調和関数  の値は,
の値は, 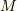 を中心とする球内(半径によらない!!)の
を中心とする球内(半径によらない!!)の  の値の平均値に等しい』という主張だと読めます.
の値の平均値に等しい』という主張だと読めます.
| [†] | これは著しく美しい調和関数の性質です.例えば,代表的な調和関数である三角関数を思い浮かべれば,周期的に変動する値を,平均値で表わすという意味が直観的に分かりやすいと思います. |
性質4
調和関数  が領域
が領域  内で定数関数ではないとすると,
内で定数関数ではないとすると,  は
は  内で最大値も最小値も取りません.
内で最大値も最小値も取りません.
proof
例えば,もし  内の点
内の点 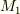 で
で  が最大値を取ったとすると,
が最大値を取ったとすると,  をすっぽり包むような
をすっぽり包むような 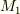 を中心とする半径
を中心とする半径  (十分大きい)の球状領域
(十分大きい)の球状領域 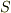 を,
を, 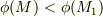 となるように取れます.ただし,
となるように取れます.ただし, 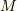 は
は 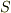 内の任意の点とします.一方,式
内の任意の点とします.一方,式 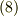 より,
より, 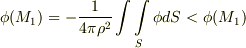 (中辺は
(中辺は 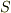 内の
内の  の平均値の意味)が要請されます.これはおかしいので,結局,
の平均値の意味)が要請されます.これはおかしいので,結局,  は最大値を取らないことになります.同様にして,最小値も取れません.■
は最大値を取らないことになります.同様にして,最小値も取れません.■
性質5【ディリクレ問題の定理】
theorem
領域  の境界は閉曲面
の境界は閉曲面 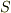 だとします.調和関数
だとします.調和関数  がもし
がもし 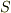 上で一定値
上で一定値  を取るなら,
を取るなら,  は
は  内の至るところで一定値
内の至るところで一定値  を取るということが言えます.
を取るということが言えます.
(式 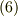 で
で 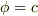 と置けば示せます.)
と置けば示せます.)
性質6
theorem
ラプラス方程式  は,境界
は,境界 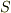 上の境界条件下に解くとき,一意的な解を持ちます.
上の境界条件下に解くとき,一意的な解を持ちます.
proof
もし  が二つの解
が二つの解 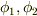 を持つとすると,ラプラス方程式の線形性より,その差
を持つとすると,ラプラス方程式の線形性より,その差 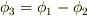 もやはりラプラス方程式を満たすはずです.ところで,境界
もやはりラプラス方程式を満たすはずです.ところで,境界 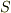 上では
上では 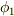 と
と 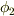 は同じ値を取るはずで,
は同じ値を取るはずで, 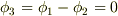 となります.すると,性質5より,
となります.すると,性質5より,  内では至るところ
内では至るところ 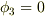 となりますので,すなわち
となりますので,すなわち 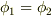 が示されます.■
が示されます.■
| [‡] | ラプラス方程式  に,境界条件として境界上の値 に,境界条件として境界上の値 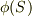 を与えて解く問題をディレクレ問題と言います.境界条件として境界上での方向微分 を与えて解く問題をディレクレ問題と言います.境界条件として境界上での方向微分 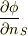 を与えて解く問題をノイマン問題と言います.いずれも物理学で重要な微分方程式ですが,ここではその解法までを示すことはしません.興味のある人は微分方程式論やポテンシャル論といった題名の教科書を当たってみて下さい. を与えて解く問題をノイマン問題と言います.いずれも物理学で重要な微分方程式ですが,ここではその解法までを示すことはしません.興味のある人は微分方程式論やポテンシャル論といった題名の教科書を当たってみて下さい. |
性質7【ノイマン問題の定理】
theorem
ラプラス方程式  が,境界
が,境界 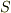 上で
上で 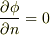 を満たすとき,
を満たすとき,  内の至るところで
内の至るところで 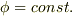 となります.
となります.
proof
これは, グリーンの第一定理 の系 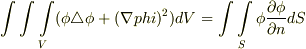 より,
より, 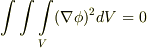 を得ます.これより
を得ます.これより 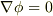 となり,積分して
となり,積分して 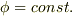 を得ます.■
を得ます.■
性質8
theorem
ラプラス方程式  の二つの解
の二つの解 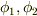 の方向微分が,境界
の方向微分が,境界 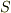 上で同一であるとき,
上で同一であるとき, 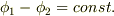 となります.
となります.
proof
二解の差 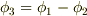 の方向微分を取って
の方向微分を取って 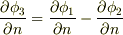 となりますが,右辺は条件より
となりますが,右辺は条件より 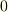 となります.これを積分すると,
となります.これを積分すると,  を得ます.■
を得ます.■
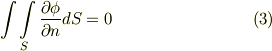
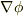 を代入して次のように変形すれば,左辺
を代入して次のように変形すれば,左辺 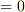 よりすぐに導けます.
よりすぐに導けます.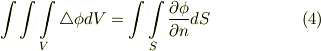
 に対し
に対し 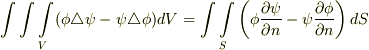 を適用すれば,左辺
を適用すれば,左辺