△

勾配のそのまた発散を取ったものを ラプラシアン と呼び， $\triangle$ で表わします．式を読むときには，「デルタ」と読む場合もあります．

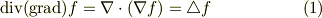
${\rm div (grad)}f = \nabla \cdot (\nabla f) = \triangle f \tag{1}$

記号でだけ考えれば， $\triangle$ は $\nabla$ の二乗（内積）と考えることも出来ます．

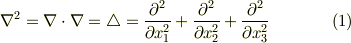
$\nabla ^{2} = \nabla \cdot \nabla = \triangle = \frac{\partial ^2}{\partial x_{1}^{2}} + \frac{\partial ^2}{\partial x_{2}^{2}} + \frac{\partial ^2}{\partial x_{3}^{2}} \tag{1}$

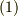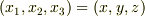ラプラシアンの定義はこれだけです．デカルト座標系の場合には，式 (1) で，単に $(x_{1},x_{2},x_{3})=(x,y,z)$ とすれば良いだけですが，一般の直交曲線座標系における表現は，ベクトル演算子の座標変換を参照してください．また，任意の多様体上での表現は多様体上のテンソル解析を参照して下さい．

ラプラス方程式と調和関数

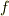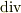式 (1) の形の微分方程式を ラプラス方程式 と呼びます．はスカラー関数なので座標不変量ですし， ${\rm grad}$ や ${\rm div}$ は gradの積分形による定義や divとrotの積分形による定義で示したように座標系の取り方によらない演算子です．（座標系の取り方によらないというのは，座標変換で不変という意味ではありません．）よって，ラプラス方程式も座標系の取り方によらない関係式で，この形に表わされた物理法則は普遍的な表現だと言えます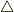． $\triangle$ の記号はいかにもシンプルで，本当にすっきりした表現だと思います．

【ラプラス方程式】

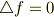
$\triangle f = 0$

ラプラス方程式を満たす関数（つまりラプラス方程式の解）を 調和関数 と呼びます．（ ポテンシャル関数 という言葉を調和関数とほぼ同義に使う人もいるようです．）この名前は，ラプラス方程式をデカルト座標系で 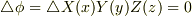$\triangle \phi = \triangle X(x)Y(y)Z(z) =0$ と変数分離形を仮定して解くと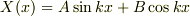， $X(x)=A\sin kx + B \cos kx$ のような正弦波状の解が得られるところから来ているようです．（ラプラス方程式の変数分離については，ラプラス方程式の変数分離を参照ください．）

そのほかにも波動方程式やヘルムホルツ方程式など，物理学で重要な様々な微分方程式がラプラシアンを使った形で表現されます．このため，ラプラシアンは物理学のあちこちに顔を出してきます．

【熱伝導方程式】

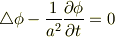
$\triangle \phi - \frac{1}{a^2}\frac{\partial \phi}{\partial t} = 0$

【波動方程式】

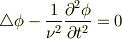
$\triangle \phi - \frac{1}{\nu^2}\frac{\partial^2 \phi}{\partial t^2} = 0$

【ヘルムホルツ方程式】

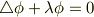
$\triangle \phi + \lambda \phi = 0$

【ポアソン方程式】

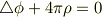
$\triangle \phi + 4\pi \rho = 0$

ラプラス方程式は，ヘルムホルツ方程式やポアソン方程式で 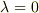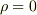$\lambda =0$ ， $\rho =0$ などとした特別な場合と見ることも出来ますね．これらの方程式の応用や解法は，また稿を改めて考えたいと思います．

歴史

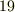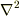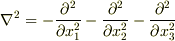ラプラシアンの記号は世紀後半頃から徐々に使われるようになりましたが，最初は $\nabla ^{2}$ と書くことの方が多かったようです．マックスウェル( $\text{James Clerk Maxwell (1831-1879)}$ )やテイト( $\text{Peter Gurthrie Tait (1831-1901)}$ )等，ベクトル解析の初期の功労者達には，四元数の演算を意識して， $\nabla ^2 =-\frac{\partial ^2}{\partial x_{1}^{2}} - \frac{\partial ^2}{\partial x_{2}^{2}}-\frac{\partial ^2}{\partial x_{3}^{2}}$ と書く人が多く，符号が今と逆になっていました．現在のように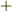で使い始めたのはケルビン卿 $(\text{William Thomson (Lord Kelvin) (1824-1907)})$ やヘヴィサイド( $\text{Oliver Heaviside (1850-1925)}$ )ですが，ラプラシアンの符号を $\pm$ 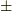どちらにすべきかという不毛な論争は長く続きました．現在の記法は，ヘヴィサイドやギブス( $\text{Josiah Willard Gibbs (1839-1903)}$ )など，電磁気学の文脈からベクトル解析を発展させた人達が整理したもので，マックスウェルやテイトの記法を踏襲しています．電磁気学とは全く関係なくベクトル解析を進歩させた，数学者のグラスマン( $\text{Hermann}$ ${\rm G\ddot{u}nter}$ $\text{Grassmann (1809-1877)}$ )やメビウス( $\text{August Ferdinand}$ ${\rm M\ddot{o}bius \ (1790-1868)}$ )らの用いた記法は，現在のものとは似ても似つかないものです．ラプラシアンは三次元ユークリッド空間に限らず，色々な次元や空間で定義可能ですが，相対性理論で使われるミンコフスキー空間上のラプラシアンは，特に $\square$ と書かれ，ダランベール演算子と呼ばれたりもします．また，ドラム( $\text{Georges de Rham (1903-1990)}$ )はラプラシアンを可微分多様体上の外微分演算子として一般化しました．ラプラシアンは形も魅力的ですが，現在でもあちこちで大活躍です．

ラプラシアンにその名を残すラプラスは，ラプラス方程式を最初に発見しましたが，ラプラスの時代にはまだベクトル解析が無かったため，私達がいま勉強している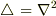， $\triangle = \nabla ^{2}$ と書けるラプラシアンを発明したわけではありません．

ラプラス

ラプラスの一生も調べてしまったので，ついでに紹介しておきます．ラプラス( $\text{Pierre-Simon Laplace (1749-1827)}$ )は，フランスのノルマンディー地方の農家に生まれました．少年時代は神学を勉強し，聖職につこうと考えていたようですが，のちに数学の才能に目覚め，十九歳でパリに出てダランベール( $\text{Jean Le Rond d'Alembert (1717-1783)}$ )に師事しました．ラプラスの業績は微分方程式，差分方程式，確率論，解析学，天文学，力学，熱力学などの多岐に渡り，特に惑星の軌道に関する研究成果によって，若くしてパリの科学アカデミーの正会員に叙せられました．アカデミーではその才能と知識を広く認められましたが，彼自身も自分の業績を誇ったことから，師のダランベールとの人間関係がこじれたりもしています．

当時一流の科学者であったラプラス．業績も大きいが，権力も振るったようだ．

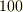この時代のフランスの科学者は，フランス革命 (1789) のために，政治とも無関係ではいられませんでした．例えば，質量保存の法則で有名な化学者ラボアジェ $(\text{Antoine Laurent Lavoisine (1743-1794)})$ は，革命政府によってギロチンで処刑されています．ラプラスは混乱期の数年間はパリから避難していましたが，のちに革命政府が合理主義精神を掲げ，分度器を一周 100 度と改める，長さの基準はメートル法を採用する，一年を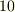ヶ月とし一日も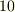時間とする，などと一連の過激とも言える改正を推し進めたとき，その天文学や科学の知識を買われて復帰（そして政界デビュー？）しました．ナポレオンの時代には，元老院議員にまで選ばれ，レジオン・ド・ヌール勲章を受けるなど，政治家としても活躍しましたが，内務省の勤務はたった六週間でクビになっています．これについて，ナポレオンは回想録の中でこう綴っています．『ラプラスは政府にまで，無限小の考えを持ち込んだから．』ラプラスは，ナポレオン時代には伯爵，ブルボン王朝復活の際には侯爵にまで列せられています．政治的嗅覚が鋭く，体制の変化にも巧みに適応したようですが，政治家としての評判はいまいちだったようです．

『全世界の原子の位置と運動量を知ることができれば，その後の世界は，これらの原子の連立運動方程式の解として未来永劫まで記述できるはずだ』という ラプラスの魔 とよばれる問題を提唱したことでも有名です．二十世紀になり，量子力学によって，原子の位置と運動量を同時に測定することはできないことが示され，ラプラスのアイデアは否定されましたが，人間機械論や唯物論的運命論といった（悲観的な）決定論的思想の科学的なバックボーンとして，この問題は量子力学登場以前の哲学界にも大きな影響を与えました．

[home] [ベクトル解析] [ページの先頭]