グリーンの定理
この記事では, ガウスの発散定理 から,グリーンの定理と呼ばれる定理を二つ導きます.既出の 平面のグリーンの定理 と区別するため,これらを グリーンの第一定理 , グリーンの第二定理 と呼ぶことにします.グリーンの第一・第二定理は,ガウスの発散定理から導かれる派生的な定理ですが,ポテンシャル理論で重要なため,それなりに有名な定理です.
グリーンの第一定理
まず, ガウスの発散定理 からスタートします.ここでは,もうガウスの発散定理について細かいことは復習しません.
theorem
- 【ガウスの発散定理】
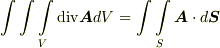
ここで特に,連続で必要なだけ微分可能な(つまり  級の)スカラー関数
級の)スカラー関数  を用いて,
を用いて, 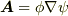 と書ける場合を考えます.このとき,ガウスの発散定理の左辺の被積分関数は次のように変形できるでしょう.
と書ける場合を考えます.このとき,ガウスの発散定理の左辺の被積分関数は次のように変形できるでしょう.
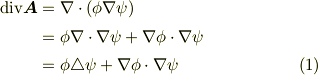
二行目は,単に積の微分則(チェーン・ルール)を使っただけですが,何と何の内積を取るのかだけ気をつけてください.一方,ガウスの発散定理の右辺の被積分関数は次のようになります.
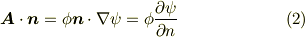
式 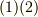 から,次の公式を得ます.これが グリーンの第一定理 です.
から,次の公式を得ます.これが グリーンの第一定理 です.
theorem
- 【グリーンの第一定理】

特に 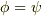 と置けば,次の定理を得ます.
と置けば,次の定理を得ます.
corollary
グリーンの第二定理
第一定理を導いたのと同様にして,今度は 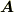 として
として 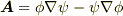 という形に書けるベクトル場を考えます.このとき,次の関係式に注意して下さい.
という形に書けるベクトル場を考えます.このとき,次の関係式に注意して下さい.
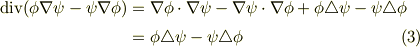
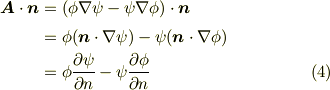
式 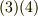 をガウスの発散定理の両辺に代入して得る関係式を, グリーンの第二定理 と呼びます.
をガウスの発散定理の両辺に代入して得る関係式を, グリーンの第二定理 と呼びます.
theorem
- 【グリーンの第二定理】
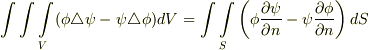
ラプラシアンの積分表示
グリーンの第一定理で 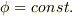 と置けば,次の形に帰着します.
と置けば,次の形に帰着します.

この両辺に 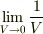 を作用させると,次のように書き換えることが出来ます.
を作用させると,次のように書き換えることが出来ます.
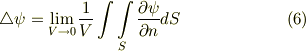
これは,ラプラシアンの作用の積分表示になっています.( gradの積分形による定義 や divとrotの積分形による定義 で,  ,
, 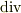 ,
, 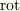 の積分表示をそれぞれ示したことを思い出してください.)右辺は,曲面
の積分表示をそれぞれ示したことを思い出してください.)右辺は,曲面 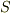 には依存しますが,座標系の取り方には依存しない形であることが分かります.これも ラプラシアンは座標系の取り方によらない ことを示す一つの例になっています.
には依存しますが,座標系の取り方には依存しない形であることが分かります.これも ラプラシアンは座標系の取り方によらない ことを示す一つの例になっています.
もう一つの定理
グリーンの第二定理から,もう一つ有用な定理が導かれます.式中,領域  は閉曲面
は閉曲面 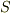 を境界とするものとし,
を境界とするものとし, 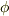 は領域
は領域  で定義される,少なくとも
で定義される,少なくとも 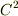 級の連続なスカラー関数とします.
級の連続なスカラー関数とします. 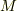 は
は  内の任意の点とし,点
内の任意の点とし,点 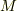 における
における 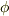 の値を
の値を 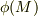 と表記します.このとき,次の関係が成り立ちます.
と表記します.このとき,次の関係が成り立ちます.
corollary
![\phi (M) = -\frac{1}{4\pi} \int \int \int \limits _{V} \frac{1}{r}\triangle \phi dV -\frac{1}{4\pi}\int \int \int \limits _{S} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] dS](./4be3a8b29c776a4e63cdfb4da3d7e2b8.png)
proof
まず 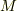 を中心とする,半径
を中心とする,半径 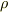 の十分に小さい球状領域を
の十分に小さい球状領域を  内に考え,その表面を
内に考え,その表面を  とします.そして
とします.そして  を
を  の内部と,外(
の内部と,外( 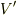 とします)に分けます.次に,グリーンの第二定理で
とします)に分けます.次に,グリーンの第二定理で 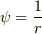 と置くと,
と置くと,  であることに注意して,
であることに注意して, ![\int \int \int \limits _{V'} \triangle \left( - \frac{1}{r} \phi \right) dV = \int \int \limits _{S} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] dS + \int \int \limits _{\varepsilon} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] d\varepsilon](./c8ddd87ddf0bda60eb49061618e43b91.png) を得ます
を得ます 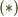 .(
.(  など,極座標における
など,極座標における  の公式は ベクトルの公式2 を参照してください.)式
の公式は ベクトルの公式2 を参照してください.)式  で,
で,  は領域
は領域 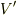 の法線方向を表わしていますが,上図のように,
の法線方向を表わしていますが,上図のように,  側では,
側では, 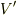 の外向き法線は
の外向き法線は  と平行で(∵
と平行で(∵  が球だから)逆向きになりますので,
が球だから)逆向きになりますので,  右辺第二項を次のように変形できます.
右辺第二項を次のように変形できます. ![\int \int \limits _{\varepsilon} \left[ \phi \frac{\partial }{\partial n} \left( \frac{1}{r} \right) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] d\varepsilon = \int \int \limits _{\varepsilon} \left[ - \phi \frac{\partial }{\partial r} \left( \frac{1}{r} \right) - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] d\varepsilon = \int \int \limits _{\varepsilon} \left[ \frac{\phi }{r^{2}} - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] d\varepsilon](./f3d5545bf365c11bcadaa7d7edfac83e.png) .次に
.次に  の極限を取ると,
の極限を取ると, ![\lim \limits _{\rho \rightarrow 0} \int \int \limits _{\varepsilon} \left[ \frac{\phi }{r^{2}} - \frac{1}{r} \frac{\partial \phi}{\partial n} \right] d\varepsilon = \lim \limits _{\rho \rightarrow 0, \ M' \rightarrow M} \left[ \frac{\phi (M')}{\rho ^{2}} - \frac{1}{\rho} \frac{\partial \phi}{\partial n} _{M'} \right] 4 \pi \rho^{2} = 4 \pi \phi (M)](./e7a5d2675439e7b1ff3963758902799b.png) を得ます
を得ます  .式
.式  でも
でも  の極限を取り,式
の極限を取り,式  を使うと定理が示されます.■
を使うと定理が示されます.■
| [*] | この定理は,任意の点におけるスカラー関数の値が,面積分や体積分だけから分かってしまうという,考えてみれば恐るべき定理です.もっとも,ストークスの定理,ガウスの発散定理,平面のグリーンの定理など,今までに勉強した積分定理はどれも『領域内部の情報が,境界を調べるだけで分かってしまう』という仕組みになっていましたので,その同系列の定理だとも考えられます. |
ちょっと長くて,覚えにくい形をしていますが,後で ヘルムホルツの定理 という,とても大事な定理を証明するときに使うので,紹介しておきました.全く同様な定理を,ベクトル値関数に対して考えることもできます.証明はほとんど同じなので省略して結果のみを示します.
![\bm{A} (M) = -\frac{1}{4\pi} \int \int \int \limits _{V} \frac{1}{r}\triangle \bm{A} dV -\frac{1}{4\pi}\int \int \limits _{S} \left[ \bm{A} \frac{\partial }{\partial n} \left( \frac{1}{r} \right ) - \frac{1}{r} (\bm{n} \cdot \nabla ) \bm{A} \right] dS](./5d3a1076fbadc506374fc51f2a985388.png)