立体角とガウスの発散定理
まず,表題の話題に入る前に,弧度法による角度(ラジアン)の意味を復習します.弧度法では,円弧と円の半径の比を角度と定義するのでした.
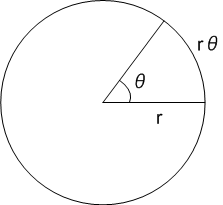
図1
この考え方は,円はどんな大きさの円であっても相似である(つまり,円という形には一種類しかない)という性質に基づいています.例えば,円の半径を  とすると,円周の長さは
とすると,円周の長さは 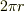 となり,『円周/半径』という比は
となり,『円周/半径』という比は  に関係なく常に
に関係なく常に 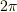 になることを読者のみなさんは御存知かと思います.
になることを読者のみなさんは御存知かと思います.
| [*] | 順序としては,円周を直径で割った値を  と定義したのが先で,円周と半径を例として挙げたのは自己反復的かも知れません.考えて欲しいのは,円周の長さと円の直径(半径でも良い)が,円の大きさに関わらず一つの定数になるという事実です. と定義したのが先で,円周と半径を例として挙げたのは自己反復的かも知れません.考えて欲しいのは,円周の長さと円の直径(半径でも良い)が,円の大きさに関わらず一つの定数になるという事実です. |
古代のエジプト人やギリシャ人は,こんなことをとっくに知っていて,  の正確な値を求めようと努力していました.
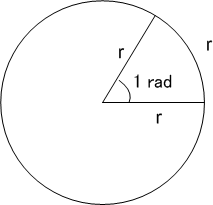
の正確な値を求めようと努力していました.  の歴史はとても面白いですが,今は脇道に逸れるので深入りしません.さて,図1のように円の二つの半径が挟む角
の歴史はとても面白いですが,今は脇道に逸れるので深入りしません.さて,図1のように円の二つの半径が挟む角 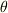 を考えるとき,その角が睨む円弧の長さ
を考えるとき,その角が睨む円弧の長さ  と角の間には比例関係がなりたつはずで,いっそのこと,角度そのものを,角が睨む円弧の長さとして定義することが出来そうです.この考え方が 弧度法 で,円の半径と同じ長さの円弧を睨むときの角を,
と角の間には比例関係がなりたつはずで,いっそのこと,角度そのものを,角が睨む円弧の長さとして定義することが出来そうです.この考え方が 弧度法 で,円の半径と同じ長さの円弧を睨むときの角を,  ラジアンと呼ぶことにします.
ラジアンと呼ぶことにします.
円弧は線分より長いので,  ラジアンは
ラジアンは 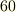 度(正三角形の角)よりほんの少し小さい.
度(正三角形の角)よりほんの少し小さい.
この定義,『半径=円弧となる角を 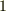 ラジアンとする』を使えば,全ての円の相似性から,円の大きさには関わりなく角度を定義できるわけです.これは,なかなか賢いアイデアです.一方,一周分の角度を
ラジアンとする』を使えば,全ての円の相似性から,円の大きさには関わりなく角度を定義できるわけです.これは,なかなか賢いアイデアです.一方,一周分の角度を 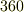 に等分する方法は 六十進法 と呼ばれます.六十進法で
に等分する方法は 六十進法 と呼ばれます.六十進法で 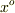 である角度は,弧度法では次のようになります.
である角度は,弧度法では次のようになります.

| [†] | 六十進法の起源は非常に古く,誰が最初に使い始めたのか分かりません.恐らく古代バビロニアに起源を発すると言われています.古代バビロニアでは精緻な天文学が発達していましたが,計算には六十進法が使われていました. 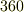 は多くの約数を持つので,実際の計算では結構便利ですが,『なぜ は多くの約数を持つので,実際の計算では結構便利ですが,『なぜ 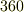 なのか?』というと,特に なのか?』というと,特に 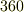 でなければならない理由はありません.(一年の日数に近いというのは大きな理由だと思われます.)ここが,六十進法の弱いところです.時計が一時間 でなければならない理由はありません.(一年の日数に近いというのは大きな理由だと思われます.)ここが,六十進法の弱いところです.時計が一時間 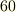 分と決まっているのも,古い六十進法の名残です.フランス革命の際,何ごとも合理化しようとした革命派は,時計も一日 分と決まっているのも,古い六十進法の名残です.フランス革命の際,何ごとも合理化しようとした革命派は,時計も一日 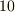 時間,角度も一周 時間,角度も一周 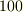 度に改めようとしましたが,あまり定着しませんでした.ラジアンは,半径と円弧の比で決める角度ですから,六十進法のような単位の不合理さはありませんが,角度を表わすのに,常に 度に改めようとしましたが,あまり定着しませんでした.ラジアンは,半径と円弧の比で決める角度ですから,六十進法のような単位の不合理さはありませんが,角度を表わすのに,常に  という無理数を使わなければならないという点が気持ち悪いと言えば気持ち悪いですね. という無理数を使わなければならないという点が気持ち悪いと言えば気持ち悪いですね. 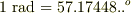 くらいになります. くらいになります. |
立体角
平面上で,円弧を睨む扇形の中心角を,円弧の長さを使って定義しました.このアイデアを全く同様に三次元に拡張したのが 立体角 です.空間上,半径 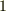 の球を考え,球の中心を頂点とするような円錐を考えます.この円錐によって切り取られる球面の面積のことを立体角と定義します.
の球を考え,球の中心を頂点とするような円錐を考えます.この円錐によって切り取られる球面の面積のことを立体角と定義します.
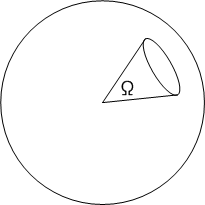
逆に,ある曲面をある点から見たときの立体角を求めることも出来ます.次図のように,点 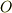 から曲面
から曲面 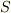 を眺めるとき,
を眺めるとき, 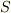 と
と 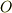 を結ぶ直線群によって,
を結ぶ直線群によって, 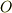 を中心とする単位球面が切り取られる面積を
を中心とする単位球面が切り取られる面積を 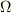 とするとき,
とするとき, 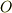 から見た
から見た  の立体角は
の立体角は  であると言います.
であると言います.
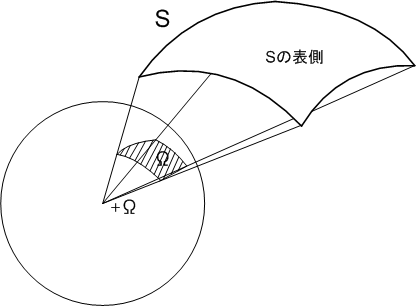
ただし,ここで考える曲面  は表と裏を区別できる曲面だとし,点
は表と裏を区別できる曲面だとし,点 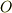 が
が 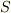 の裏側にあるとき
の裏側にあるとき 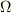 ,点
,点 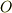 が
が 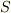 の表側にあるとき
の表側にあるとき  として,立体角には
として,立体角には 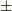 の符号をつけることにします.
の符号をつけることにします.
ガウスの発散定理と立体角
曲面 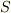 上に,点
上に,点 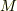 を中心とする微小面積
を中心とする微小面積 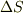 を取り,その法線ベクトルを
を取り,その法線ベクトルを 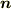 とします.ベクトル
とします.ベクトル 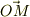 を
を  と置き,
と置き,  と
と 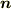 のなす角を
のなす角を 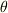 とします.
とします.  とします.
とします.
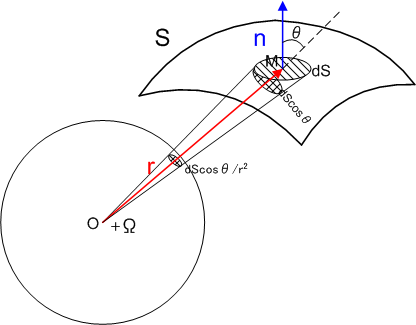
このとき,  を十分小さい面積だとして,ほぼ平らと見なすと,近似的に
を十分小さい面積だとして,ほぼ平らと見なすと,近似的に 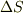 の立体角
の立体角 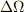 は次のように表現できます.(なんでこうなるのか,上図を見て考えてみて下さい.)
は次のように表現できます.(なんでこうなるのか,上図を見て考えてみて下さい.)

式 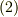 で
で 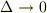 なる極限を取り,
なる極限を取り, 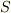 と
と 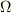 の全微分
の全微分 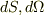 を考えれば,式
を考えれば,式 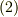 は近似ではなく,微小量に関する等式になります.
は近似ではなく,微小量に関する等式になります.
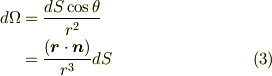
従って,曲面  全体の立体角は式
全体の立体角は式 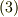 を積分して得られます.
を積分して得られます.
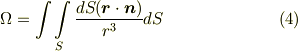
閉曲面の立体角
次に,式 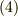 の積分領域
の積分領域 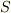 が,閉曲面である場合を考えてみましょう.後で,
が,閉曲面である場合を考えてみましょう.後で, 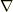 に関して,次の関係式を使います.
に関して,次の関係式を使います.


極座標系での 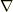 の公式はまだ勉強していませんが, ベクトルの公式2 を参考にして下さい.とりあえず,式
の公式はまだ勉強していませんが, ベクトルの公式2 を参考にして下さい.とりあえず,式 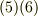 は了承して先に進むことにします.まず,立体角の中心点
は了承して先に進むことにします.まず,立体角の中心点 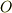 が閉曲面の外にある場合を考えます.このとき,式
が閉曲面の外にある場合を考えます.このとき,式 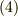 の積分は次のように変形できます.二行目から三行目への式変形には ガウスの発散定理 を使います.
の積分は次のように変形できます.二行目から三行目への式変形には ガウスの発散定理 を使います.

すなわち, 閉曲面全体の立体角は,外部の点Oから測る場合,Oの場所に関わらず常に零になる ということが分かりました.この結果は,次のように直観的に了解することも出来ます.
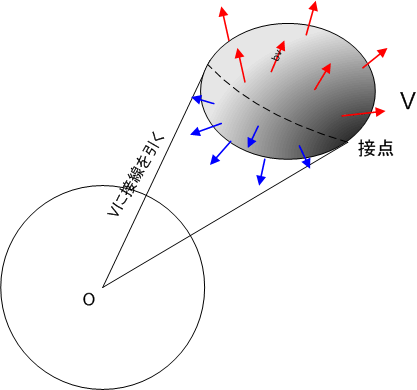
上図のように,一点 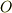 から閉曲面
から閉曲面 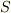 の周囲にグルリ接線を引くとき,
の周囲にグルリ接線を引くとき, 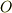 の位置に関わらず,必ず
の位置に関わらず,必ず 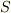 によって囲まれる領域
によって囲まれる領域  をこれらの接線の接点によって,『手前側』と『向こう側』に二分できます.そして,手前側と向こう側では法線ベクトルが逆向きを向くわけですから(図の赤い矢印と青い矢印),これらの和が零になるというも納得がいきませんか?
をこれらの接線の接点によって,『手前側』と『向こう側』に二分できます.そして,手前側と向こう側では法線ベクトルが逆向きを向くわけですから(図の赤い矢印と青い矢印),これらの和が零になるというも納得がいきませんか?
逆に, 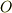 が
が  の内部にある場合は,少し工夫が必要です.次図のように,
の内部にある場合は,少し工夫が必要です.次図のように, 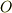 を中心とする半径
を中心とする半径  の球面
の球面 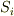 を考えましょう.
を考えましょう. 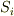 の内部の領域を
の内部の領域を 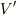 とします.
とします.

ここで 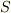 と
と 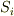 を境界とする領域(つまり
を境界とする領域(つまり 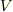 から
から 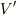 を抜いた領域です)を考え,
を抜いた領域です)を考え, 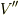 となづけます.(
となづけます.( 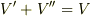 です.)
です.) 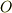 は,
は, 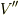 から見れば
から見れば 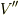 の外にありますから,式
の外にありますから,式 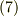 より,
より,  の立体角は
の立体角は 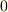 になるはずです.
になるはずです.
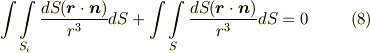
一方, 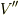 の
の 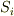 上での単位法線ベクトル
上での単位法線ベクトル 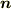 は,向きは
は,向きは 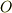 に向かう向きですが
に向かう向きですが  と逆向きです.(
と逆向きです.( 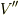 の表面から外に向かう方向を法線ベクトルの正と定めたからです.)この点に注意すると,
の表面から外に向かう方向を法線ベクトルの正と定めたからです.)この点に注意すると, 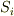 表面では
表面では 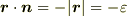 がなりたちます.これより,式
がなりたちます.これより,式 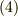 は次のようになります.
は次のようになります.

つまり, 閉曲面Sの立体角Ωを内部から測った場合,曲面の形によらず,立体角は4πになる ということが分かりました.これは大変重要な結果です.
【閉曲面の立体角】
