接線，主法線，従法線

弧長パラメータで表わした空間曲線 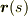$\bm{r}(s)$ を考えます．

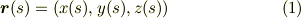
$\bm{r} (s) =(x(s),y(s),z(s)) \tag{1}$

ただし，接ベクトル 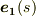$\bm{e_{1}}(s)$ の大きさはだとします．つまり，弧長パラメーターで考えた速度ベクトルが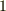だということです．

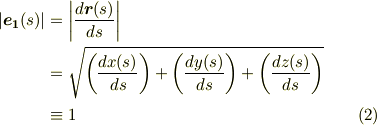
$|\bm{e_{1}}(s)| &= \left| \frac{d\bm{r}(s)}{ds} \right| \\&= \sqrt{\left( \frac{dx(s)}{ds}\right) + \left( \frac{dy(s)}{ds}\right) + \left( \frac{dz(s)}{ds}\right) } \\ & \equiv 1 \tag{2}$

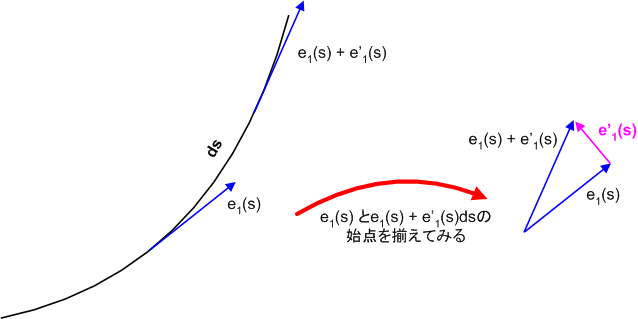
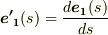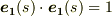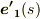このとき，加速度ベクトル $\bm{{e'}_{1}}(s) =\frac{d\bm{e_{1}}(s)}{ds}$ を考えてみましょう．少しトリッキーですが， $\bm{e_{1}}(s) \cdot \bm{e_{1}}(s) = 1$ の両辺をで微分することで $\bm{{e'}_{1}}(s)$ の向きが分かります．

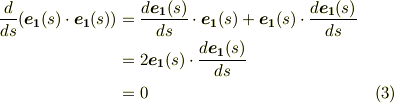
$\frac{d}{ds}(\bm{e_{1}}(s) \cdot \bm{e_{1}}(s)) & = \frac{d\bm{e_{1}}(s)}{ds} \cdot \bm{e_{1}}(s) + \bm{e_{1}}(s) \cdot \frac{d\bm{e_{1}}(s)}{ds} \\ &= 2 \bm{e_{1}}(s) \cdot \frac{d\bm{e_{1}}(s)}{ds} \\ & = 0 \tag{3}$

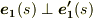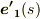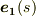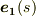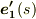これより $\bm{e_{1}}(s) \perp {\bm{e'_{1}}(s)}$ ，つまり， $\bm{{e'}_{1}}(s)$ は $\bm{e_{1}}(s)$ に直交していることが分かります．物理的な意味を考えてみると『接線ベクトル $\bm{e_{1}}(s)$ が，の変化に応じてどれくらい向きを変えるか』を表わしたのが ${\bm{e'_{1}}(s)}$ だと言えるでしょう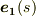． $\bm{e_{1}}(s)$ の向きが変わっていく方向は，もちろん『曲線のカーブの内側』の方向です．そして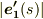， $|\bm{e'_{1}}(s) |$ の大きさが大きければ大きいほど，カーブはきつく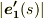， $| \bm{e'_{1}}(s) |$ が小さければカーブは緩いことが分かると思います．

この意味で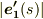， $|\bm{e'_{1}}(s) |$ を曲線の曲率と呼びます．

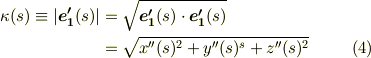
$\kappa (s) \equiv | \bm{e'_{1}}(s)| & = \sqrt {\bm{e'_{1}}(s) \cdot \bm{e'_{1}}(s)} \\ & = \sqrt {x''(s)^2 + y''(s)^{s} + z''(s)^{2}} \tag{4}$

そして，加速度ベクトル 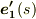$\bm{e'_{1}}(s)$ の大きさを正規化したベクトルを 主法線ベクトル と呼びます．ここでは 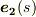$\bm{e_{2}}(s)$ と名付けます．

$\bm{e_{2}}(s) = \frac{\bm{e'_{1}}(s)}{\kappa (s)} \tag{5}$

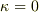（直線の場合， $\kappa = 0$ となってしまうので，式 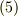(5) の定義からでは主法線ベクトルが決まりませんが，この場合は後述します．）

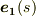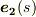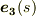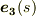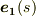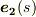接線ベクトル $\bm{e_{1}}(s)$ と主法線ベクトル $\bm{e_{2}}(s)$ という，直交する単位ベクトルを曲線上の点に対して定義することが出来ましたので，少し欲を出して，もう一つ単位ベクトルを考えることで，正規直交座標系を作りましょう．次式を満たす向きに単位ベクトル $\bm{e_{3}}(s)$ を取り，これを 従法線 と名づけることにします． $\bm{e_{3}}(s)$ は， $\bm{e_{1}}(s)$ と $\bm{e_{2}}(s)$ が張る平面に対して垂直な向きを向きます．

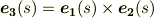
$\bm{e_{3}}(s) = \bm{e_{1}}(s) \times \bm{e_{2}}(s)$

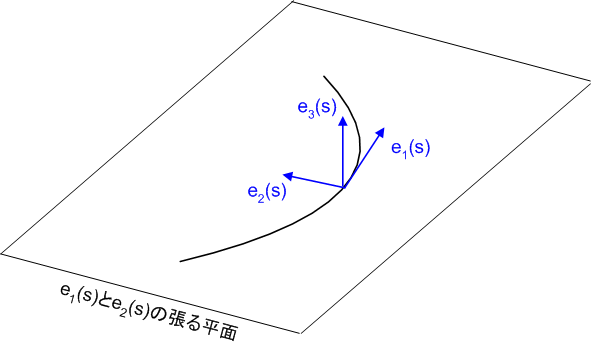
空間曲線上の点に，このようにして設定された 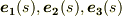$\bm{e_{1}}(s),\bm{e_{2}}(s),\bm{e_{3}}(s)$ を， フレネの標構 と呼びます．また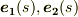， $\bm{e_{1}}(s),\bm{e_{2}}(s)$ を含む平面を 接触平面 と呼びます．

[home] [ベクトル解析] [ページの先頭]