双対基底の図形的関係
ベクトル 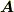 を表すのに, 共変基底 (添字が右下についた基底)を使う表現と, 反変基底 (添字が右上についた表現)を使う表現とがありました.共変基底と反変基底を互いに 双対基底 と呼ぶのでした.また,添字が右上についた成分
を表すのに, 共変基底 (添字が右下についた基底)を使う表現と, 反変基底 (添字が右上についた表現)を使う表現とがありました.共変基底と反変基底を互いに 双対基底 と呼ぶのでした.また,添字が右上についた成分 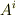 を 反変成分 ,右下についた成分
を 反変成分 ,右下についた成分 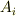 を 共変成分 と呼びます.
を 共変成分 と呼びます.
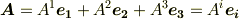
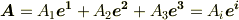
一般にベクトル 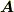 を成分表示するのに,基底に取るベクトルは独立なものならば何でも良いわけですが,異なる基底で表現すれば成分も変わってくる,というのは当然のことです.しばらくベクトル空間や双対空間など抽象的な議論ばかりが続きましたので,双対基底をなんだか鏡の国の向こうの話のように感じているいる人がいるかも知れません.背後にあった代数的な構造は抽象的でしたが,幾何ベクトルに戻れば,普通に双対基底を使ってベクトルを見たり描いたりできます.ここらで双対基底を図形的にイメージし,理解の定着を図りたいと思います.
を成分表示するのに,基底に取るベクトルは独立なものならば何でも良いわけですが,異なる基底で表現すれば成分も変わってくる,というのは当然のことです.しばらくベクトル空間や双対空間など抽象的な議論ばかりが続きましたので,双対基底をなんだか鏡の国の向こうの話のように感じているいる人がいるかも知れません.背後にあった代数的な構造は抽象的でしたが,幾何ベクトルに戻れば,普通に双対基底を使ってベクトルを見たり描いたりできます.ここらで双対基底を図形的にイメージし,理解の定着を図りたいと思います.
私達は,双対基底の間には 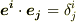 という関係がなりたつことを勉強しました.(双対基底の定義はこれだけでした.この式を見て『アッ!線形汎関数だ』と思えた人はなかなかです.)この式の意味する様子が分かりやすいよう,二次元で実際に図示してみたのが次図です.
という関係がなりたつことを勉強しました.(双対基底の定義はこれだけでした.この式を見て『アッ!線形汎関数だ』と思えた人はなかなかです.)この式の意味する様子が分かりやすいよう,二次元で実際に図示してみたのが次図です. 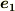 軸と
軸と 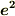 軸,
軸, 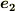 軸と
軸と 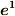 軸がそれぞれ直交していることに注意してください.
軸がそれぞれ直交していることに注意してください.
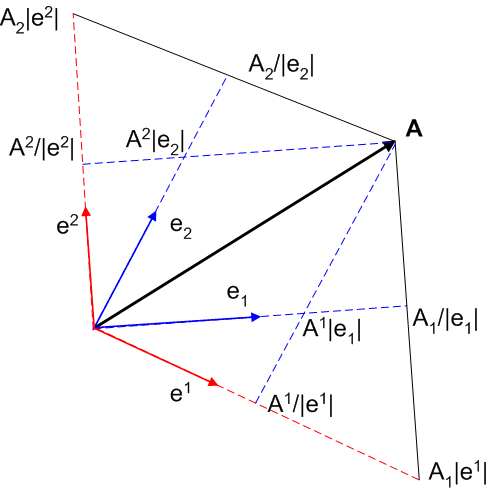
図中,線に沿って書き込んであるのはベクトルの成分ではなくて実際の長さです.一般に基底は単位ベクトルではありませんので, 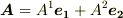 だからと言って,例えば
だからと言って,例えば 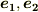 軸の張る平行四辺形の辺の 長さ は
軸の張る平行四辺形の辺の 長さ は 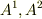 ではないことに注意してください.平行四辺形の辺の長さは,長さの定義より内積を使って
ではないことに注意してください.平行四辺形の辺の長さは,長さの定義より内積を使って 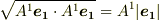 と表現されます.( 内積空間 参照.)普段,私たちは単位ベクトルを使うことが多いのでちょっと混乱した人がいると思いますが,これを機会に,ベクトルの成分とベクトルの射影長さの違いもしっかり整理してみてください.
と表現されます.( 内積空間 参照.)普段,私たちは単位ベクトルを使うことが多いのでちょっと混乱した人がいると思いますが,これを機会に,ベクトルの成分とベクトルの射影長さの違いもしっかり整理してみてください.
この図をじっくり見ていると,色々なことが見えてきます.例えば, 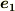 と
と 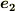 をグーッと開いていって直交させると,
をグーッと開いていって直交させると, 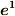 と
と 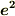 はどうなるか,点線で描いた平行四辺形や長方形はどのようになるか,逆に
はどうなるか,点線で描いた平行四辺形や長方形はどのようになるか,逆に 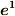 と
と 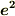 を閉じていくと,
を閉じていくと, 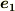 と
と 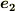 はどうなるか等を想像して,色々な考察を巡らしてみてください.
はどうなるか等を想像して,色々な考察を巡らしてみてください. 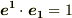 ,
, 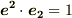 の関係を忘れないようにしてください.
の関係を忘れないようにしてください.
| [*] | 反変ベクトルと共変ベクトルは,ちょうど全てが裏返しになった双子の兄弟のような関係にあるとことに気がつくと思います.図をみれば,直交する二つの基底で,添字の上下や添字の番号( 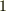 か か 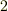 )がちょうど逆になっていることや,『反変基底の張る角度が鋭角ならば,共変基底は鈍角』と,角度までも裏返しになっていることが分かるでしょう.まさに双対です. )がちょうど逆になっていることや,『反変基底の張る角度が鋭角ならば,共変基底は鈍角』と,角度までも裏返しになっていることが分かるでしょう.まさに双対です. |
| [†] | 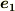 と と 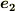 ,もしくは ,もしくは 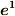 と と 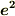 が直交する場合, が直交する場合, 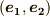 と と 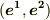 が同一になることがイメージできれば,この記事の内容の理解は大丈夫です.(^^) が同一になることがイメージできれば,この記事の内容の理解は大丈夫です.(^^) |