双対基底と双対空間
ここまでに,双対基底という添字の上下の異なる二種類の基底ベクトルが出てきました.二つの双対基底 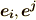 は,次の性質を満たすのでした.
は,次の性質を満たすのでした.

ここまでの流れで,勘の良い人は何となく気づいてきているかも知れませんが, 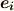 があるベクトル空間
があるベクトル空間  の基底だとすると,
の基底だとすると, 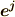 はその双対空間
はその双対空間 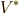 の基底になっています.双対空間の定義に戻り,
の基底になっています.双対空間の定義に戻り, 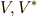 の基底で式
の基底で式 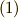 の関係がなりたつものを考えてみましょう.
の関係がなりたつものを考えてみましょう.
双対空間の基底
まず 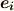 をベクトル空間
をベクトル空間  の基底とします.つまり,
の基底とします.つまり,  に属する任意の元
に属する任意の元 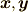 は,適当なスカラー
は,適当なスカラー 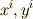 を使って次のように表現できるということです.
を使って次のように表現できるということです.
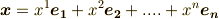
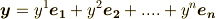
これより,和  やスカラー積
やスカラー積 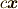 は次のように表わされます.
は次のように表わされます.

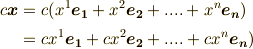
さて,  の元が表現できたので,さっそくこれに線形汎関数を作用させることを考えます.『ベクトルを一つの実数に対応させる』と言っても色々な写像が考えられますが,
の元が表現できたので,さっそくこれに線形汎関数を作用させることを考えます.『ベクトルを一つの実数に対応させる』と言っても色々な写像が考えられますが, 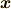 を,
を, 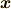 の第
の第 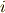 成分,すなわち
成分,すなわち 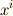 に対応させる写像を考えてみましょう.これを
に対応させる写像を考えてみましょう.これを 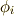 と名づけます.
と名づけます.
この写像 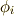 は,確かに線形汎関数です.
は,確かに線形汎関数です. 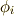 が,線形写像の定義(次式)を満たすことを確認してみて下さい.
が,線形写像の定義(次式)を満たすことを確認してみて下さい.
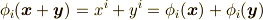
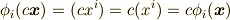
『ベクトル 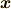 に第
に第 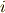 成分
成分 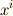 を対応させる線形写像』同士が,加法とスカラー積に関して閉じていることも明らかで,このような写像は
を対応させる線形写像』同士が,加法とスカラー積に関して閉じていることも明らかで,このような写像は 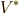 の元になることが言えます.
の元になることが言えます.
写像であることの雰囲気を出すために 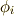 と書きましたが,今度は
と書きましたが,今度は 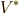 の元である雰囲気を出すために
の元である雰囲気を出すために 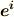 と書き直しましょう.
と書き直しましょう. 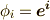 です.
です.
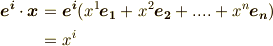
両辺を見比べて,次式が要請されます.

逆に 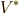 の元を
の元を 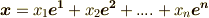 と表わすとき,式
と表わすとき,式 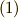 を使って次式がなりたちます.
を使って次式がなりたちます.
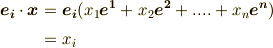

なんと, 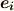 と
と 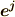 は見事に双対基底になっています.
は見事に双対基底になっています.
まとめ
最初は天下り的に  を定義として登場した双対基底でしたが,ベクトル空間とその双対空間という視点から,ベクトル空間
を定義として登場した双対基底でしたが,ベクトル空間とその双対空間という視点から,ベクトル空間  の元
の元 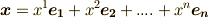 をその第
をその第 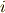 成分
成分 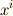 に対応させる線形汎関数の作る双対空間
に対応させる線形汎関数の作る双対空間 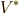 の基底として,
の基底として, 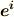 を定義できることを確認しました.
を定義できることを確認しました.
ここに出てきた『ベクトル 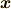 をその第
をその第 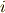 成分
成分 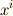 に対応させる写像』を,しばしば 射影 と呼びます.第
に対応させる写像』を,しばしば 射影 と呼びます.第 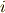 成分だけを取り出すという操作は,ベクトルを第
成分だけを取り出すという操作は,ベクトルを第 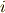 基底に射影することと同じだからです.一般にある軸に対する射影は『(第一基底への射影)+(第二基底への射影)+・・・+(第
基底に射影することと同じだからです.一般にある軸に対する射影は『(第一基底への射影)+(第二基底への射影)+・・・+(第 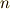 基底への射影)』といった具合に,各軸への射影の線形結合で表現できますから,
基底への射影)』といった具合に,各軸への射影の線形結合で表現できますから, 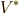 の元が一般に
の元が一般に 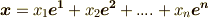 の形に書けるのも納得のいくことです.
の形に書けるのも納得のいくことです.
もちろん,双対ですからまったく逆の見方も可能で, 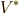 の元に対し
の元に対し  の基底
の基底 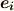 は『第
は『第 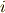 番目の成分を取り出す』という射影関数として働いています.
番目の成分を取り出す』という射影関数として働いています.
| [*] | この記事では,双対基底の位置づけを明らかにするという目的のため,最終的に射影関数による双対空間だけに話題を絞り込みましたが,双対の考え方は数学のあらゆる分野で非常に重要であり,双対空間の概念も至るところに顔を出します.抽象的な議論が苦手な人も,これを機会に双対空間に馴染んで頂ければとても嬉しいです. |
| [†] | 双対基底のアイデアを応用した例として,結晶学にでてくる直接格子と逆格子の基本ベクトルがあります.直接格子空間と逆格子空間はちょうど双対空間の関係になっています.興味のある方は,結晶学の教科書を紐解いてみて下さい.双対空間の概念を抽象的に導いた後だと,もとの空間と双対空間がまるで別世界のように感じるかも知れませんが,必ずしもそうとは限りません.基底の取り方が双対になっているということは世界の違いを意味するのではなく,視点の違いを示すだけだからです.双対空間の考え方が具体的に応用されているのを見れば,ますます理解が深まるのではないでしょうか. 双対基底の図形的関係 では,双対基底の図形的関係を視覚的関係を考えます. |