共変ベクトルと反変ベクトル
最初に,これから勉強することの予告を兼ねて,少し表記に関する約束事をしておきます.この記事には,座標系の基底として 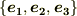 のように添字が右下につくタイプのものと,
のように添字が右下につくタイプのものと, 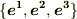 のように添字が右上につくタイプのものが両方でてきます.
のように添字が右上につくタイプのものが両方でてきます.
ベクトルをどの座標系で見るのも自由ですから,どちらを基底に使っても良いのですが,『ベクトルの成分につく添字は,基底についている添字と上下を逆にする』と約束しておきます.例えば,こんな具合です.
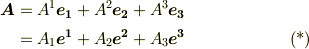
式中の 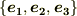 と
と 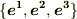 は一般に異なりますから,上付きの成分
は一般に異なりますから,上付きの成分 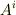 と下付きの成分
と下付きの成分  も違うものです.これは単なる表記の約束事ですから,『ふ〜ん,そういうもんかいな』と思っておいて頂ければとりあえず結構です.ただし,このように約束しておくと大変便利である,ということの理由が,だんだん分かってくると思います.
も違うものです.これは単なる表記の約束事ですから,『ふ〜ん,そういうもんかいな』と思っておいて頂ければとりあえず結構です.ただし,このように約束しておくと大変便利である,ということの理由が,だんだん分かってくると思います.
| [*] | 最初は 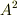 のように書くのが『 のように書くのが『  の二乗』と紛らわしくて気持ちが悪い人がいるかも知れません.しかし,実際にベクトルの計算をしていて, の二乗』と紛らわしくて気持ちが悪い人がいるかも知れません.しかし,実際にベクトルの計算をしていて,  を二乗だと思うような人はいません.文脈があれば大丈夫です. を二乗だと思うような人はいません.文脈があれば大丈夫です. |
共変ベクトル
基底ベクトルの座標変換は, 基底の座標変換 で勉強したように,最初の座標の基底ベクトルを 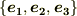 ,新しい座標の基底ベクトルを
,新しい座標の基底ベクトルを  として,次のように書けます.
として,次のように書けます.

右辺はアインシュタインの縮約により, 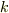 に関する総和を意味していることに注意してください.
に関する総和を意味していることに注意してください.
座標の基底ベクトルを 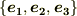 から
から  へ変換したとき,次のような,式
へ変換したとき,次のような,式 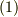 の基底ベクトルと同一の変換式に従うベクトル
の基底ベクトルと同一の変換式に従うベクトル 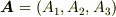 を 共変ベクトル と呼びます.基底と"同じ"変換式に従うので,"共変"と呼ぶのだそうです.
を 共変ベクトル と呼びます.基底と"同じ"変換式に従うので,"共変"と呼ぶのだそうです.

いま,いきなり成分だけで 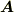 を表現しましたが,基底ベクトルを明示的に書くとすると,最初に決めた添字を上下に分けるという約束により,
を表現しましたが,基底ベクトルを明示的に書くとすると,最初に決めた添字を上下に分けるという約束により,  となるはずです.
となるはずです. 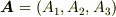 の基底ベクトル
の基底ベクトル 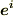 の添字は上付になってます.
の添字は上付になってます.
反変ベクトル
一方,次式のように式 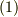 と添字の上下を逆転させた変換に従うベクトルを 反変ベクトル と呼びます.
と添字の上下を逆転させた変換に従うベクトルを 反変ベクトル と呼びます.

反変ベクトルの方も同じく,式 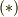 の形で基底ベクトルを明示的に表わすと,
の形で基底ベクトルを明示的に表わすと, 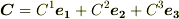 となります.
となります. 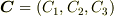 の基底ベクトル
の基底ベクトル 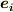 の添字は下付になっています.
の添字は下付になっています.
変換係数 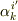 の添字が,共変ベクトルの変換係数とはちょうど上下逆になっていることに注意してください.この違いが,共変ベクトルと反変ベクトルの座標変換を表わす式形の本質的な違いです.
の添字が,共変ベクトルの変換係数とはちょうど上下逆になっていることに注意してください.この違いが,共変ベクトルと反変ベクトルの座標変換を表わす式形の本質的な違いです.
まとめ
右下に添字がつくものの変化を 共変 ,右上に添字がつくものの変化を 反変 と定義しました. 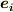 を共変基底,
を共変基底,  を共変成分,
を共変成分, 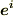 を反変基底,
を反変基底, 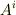 を反変成分と呼びます.この定義は,座標変換を表わす式の,式形の違いによるものでした.
を反変成分と呼びます.この定義は,座標変換を表わす式の,式形の違いによるものでした.
また,共変基底は反変成分と,反変基底は共変成分と組み合わせて使うことを最初に決めました.
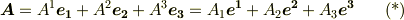
共変と反変は,ちょうど刺し違えたように対称な構造になっているようです.このような相互的な関係を,数学では 双対 と言います.双対性に関しては,また章を改めて詳しく説明する予定です.この記事の主目的は,共変ベクトル・反変ベクトルという名前と,その定義式 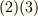 を導入することだけですので,ここまでの内容が理解できれば,まずは問題ありません.
を導入することだけですので,ここまでの内容が理解できれば,まずは問題ありません.
しかし,鋭い人はここまでに次のような疑問点を持ったことと思います.
- どうして基底と成分の添字が上下別のものを組み合わせるのか?(式
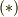 のようにする理由)
のようにする理由) - 共変基底と共変成分,反変基底と反変成分という組み合わせは無理なのか?
- 一体全体,共変ベクトルと反変ベクトルの区別とは何なのか?
共変基底と反変基底は,添字の上下が異なるものとして別々に出てきましたので,お互いにどのような関係で結ばれているのかはまだ勉強していません.この二つの基底の関係は次の 双対基底 で勉強しますが,実は共変基底と反変基底は相互に交換することが可能で,その公式を使えば共変基底と共変成分,反変基底と反変成分という組み合わせでベクトルを表記することも可能です.しかしその場合,成分の前に変換係数がごちゃごちゃ出てきます.変換係数なしに 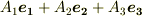 ,
, 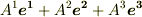 などと書くと,
などと書くと, 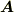 と別のものになってしまいますので注意してください.共変成分と反変成分を入れ替える公式は ベクトル成分の座標変換 で勉強します.先は長いです.
と別のものになってしまいますので注意してください.共変成分と反変成分を入れ替える公式は ベクトル成分の座標変換 で勉強します.先は長いです.
この記事の後半では疑問点  に答えるべく,共変ベクトルと反変ベクトルの違いが実感できるような実例を幾つか考えます.また,これは予告になりますが,この後 ベクトル空間と線形写像 , 双対空間 の記事では,純数学的な視点から,共変基底と反変基底の双対性の背後にある数学的構造を考察し, 双対基底と双対空間 では,こうした構造を反映として共変基底と反変基底が自然に定義できることを勉強する予定です.少し議論は抽象的になりますが,二種類の基底が出てくる理由を納得するには,一番説得力のあるアプローチだと思います.
に答えるべく,共変ベクトルと反変ベクトルの違いが実感できるような実例を幾つか考えます.また,これは予告になりますが,この後 ベクトル空間と線形写像 , 双対空間 の記事では,純数学的な視点から,共変基底と反変基底の双対性の背後にある数学的構造を考察し, 双対基底と双対空間 では,こうした構造を反映として共変基底と反変基底が自然に定義できることを勉強する予定です.少し議論は抽象的になりますが,二種類の基底が出てくる理由を納得するには,一番説得力のあるアプローチだと思います.
| [†] | 基底にも共変基底と反変基底があり,どちらも対等な対称な構造になっているわけですから,『基底ベクトルの変換と一緒だから"共変"』などという命名法は非常に根拠が曖昧です.これは慣用的に,共変基底をメインに使うことが多いという事情に由来するもののようです.共変基底と反変基底には,どちらを主従と決める確たる基準はありませんので,反変という用語は反変ベクトルに対して少し不公平な気がします.反変ベクトルから見れば,共変ベクトルが反対なんです. |
| [‡] | 共変ベクトルでも反変ベクトルでもないベクトルも世の中にはありますが,しばらくそのようなベクトルは考えません. |
具体例
変換係数を 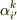 のように,正体不明の係数として表現している限り,共変ベクトルと反変ベクトルの違いは,添字の上下によるだけのもので,非常に形式的な,記号だけの違いに思えます.式
のように,正体不明の係数として表現している限り,共変ベクトルと反変ベクトルの違いは,添字の上下によるだけのもので,非常に形式的な,記号だけの違いに思えます.式 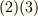 は極めて抽象的な変換式になっていますから, このままでは実際的な意味を考えることは難しいと思います.しかし,数学的に式
は極めて抽象的な変換式になっていますから, このままでは実際的な意味を考えることは難しいと思います.しかし,数学的に式 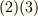 と同型の変換式に従うベクトルがあれば,それらも共変ベクトル,反変ベクトルと呼べますので,変換係数をもう少し意味の分かりやすい形に対応させて考えることができると思います.これから共変ベクトルと反変ベクトルの具体例を考えることにしましょう.
と同型の変換式に従うベクトルがあれば,それらも共変ベクトル,反変ベクトルと呼べますので,変換係数をもう少し意味の分かりやすい形に対応させて考えることができると思います.これから共変ベクトルと反変ベクトルの具体例を考えることにしましょう.
慣例に従って基底ベクトルには共変基底 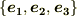 を取り,座標成分には反変成分
を取り,座標成分には反変成分 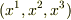 を考えます
を考えます 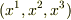 から
から 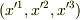 に座標変換する場合,座標成分は次の変換式に従います.(式
に座標変換する場合,座標成分は次の変換式に従います.(式 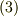 です.)
です.)
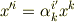
両辺を 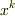 で偏微分して次式を得ます.
で偏微分して次式を得ます.

同様に 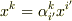 より次式を得ます.
より次式を得ます.

式 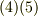 で変換係数と偏導関数の対応が一対一につきましたから,変換係数の代わりに偏導関数を使い,次式の変換式に従うベクトル
で変換係数と偏導関数の対応が一対一につきましたから,変換係数の代わりに偏導関数を使い,次式の変換式に従うベクトル 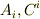 を考えるとき,これらはそれぞれ共変ベクトルと反変ベクトルだと考えることができます.
を考えるとき,これらはそれぞれ共変ベクトルと反変ベクトルだと考えることができます.


私達はいま,座標変換につられてベクトル成分がどう変わるかを知りたいわけですから,その変換係数(つまり比例係数)が, 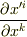 や
や 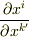 といった,座標成分の変化の関係を表わす偏微分によって表現されるという点は,直観的にも了解しやすいのではないでしょうか.
といった,座標成分の変化の関係を表わす偏微分によって表現されるという点は,直観的にも了解しやすいのではないでしょうか.
では,まず反変ベクトルの例から見てみましょう.
| [§] | 式 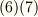 に出てくる偏導関数は,通常の一次変換では定数になります.また, に出てくる偏導関数は,通常の一次変換では定数になります.また, 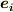 の座標系と の座標系と 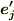 の相対的な関係が時々刻々変わる場合,つまり運動している観測者に対する座標変換では, の相対的な関係が時々刻々変わる場合,つまり運動している観測者に対する座標変換では, 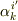 は定数ではなく時間の関数になります.そういったケースが相対性理論に出てきますが,いまは変換係数を単なる定数だと考えておいても本質的な理解の幅を狭めることはないと思います. は定数ではなく時間の関数になります.そういったケースが相対性理論に出てきますが,いまは変換係数を単なる定数だと考えておいても本質的な理解の幅を狭めることはないと思います. |
反変ベクトルの例1
反変ベクトルの例として一番重要なのは,普通の成分ベクトルです.基底ベクトルを 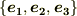 と取るとき,任意のベクトル
と取るとき,任意のベクトル 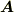 は次式のように書けます.
は次式のように書けます.
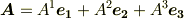
ここで考えた基底は,共変ベクトルであることを念頭に置いておいて下さい.
個々の成分は単なる実数ですが,これを3つ一組に見ると 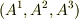 はベクトルだと考えることができます.既に添字を右上に書いてあるので,反変ベクトルであることを示しているわけですが,本当に成分ベクトルが反変ベクトルであることを以下に確認しましょう.
はベクトルだと考えることができます.既に添字を右上に書いてあるので,反変ベクトルであることを示しているわけですが,本当に成分ベクトルが反変ベクトルであることを以下に確認しましょう.
成分の変換は, 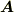 を二つの基底
を二つの基底 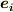 と
と 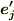 で表し,変換の式を代入してから両辺を比べることで求められるでしょう.基底は共変基底なので,逆変換を
で表し,変換の式を代入してから両辺を比べることで求められるでしょう.基底は共変基底なので,逆変換を 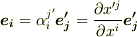 と表すことを途中で使います.
と表すことを途中で使います.

この結果と  の各成分を比べて,次式を得ます.
の各成分を比べて,次式を得ます.
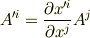
たしかに反変ベクトルの定義式 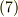 の形になっています. 共変基底の成分ベクトルは,反変ベクトルである ということが分かりました.
の形になっています. 共変基底の成分ベクトルは,反変ベクトルである ということが分かりました.
途中で共変基底の逆変換を代入したことから,この結果は形式的には当然ではありますが,意味を多少考察してみましょう.繰り返しになりますが,座標変換とはベクトルを観察する視点を変更することであって,ベクトルそのものの本当の長さを変えることではありません.あくまで,観察者の見方の変化です.

このことが分かっていれば,同じベクトルの長さを表現するのに『基底ベクトルの長さ(基準)が 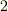 倍になれば,座標成分(見え方)は
倍になれば,座標成分(見え方)は 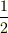 に』『基底ベクトルの長さ(基準)が
に』『基底ベクトルの長さ(基準)が  倍になれば,座標成分(見え方)は
倍になれば,座標成分(見え方)は 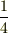 に』と,基底ベクトルの長さと,その座標における座標成分とは反比例の関係にならなければ,本当のベクトルの長さを不変に保てないことが分かると思います.『本当のベクトルの長さは座標系によらない』ということを覚えていれば,基底ベクトルの座標変換と成分の座標変換が,ちょうど逆の関係になることが,むしろ当然のように思えてこないでしょうか.
に』と,基底ベクトルの長さと,その座標における座標成分とは反比例の関係にならなければ,本当のベクトルの長さを不変に保てないことが分かると思います.『本当のベクトルの長さは座標系によらない』ということを覚えていれば,基底ベクトルの座標変換と成分の座標変換が,ちょうど逆の関係になることが,むしろ当然のように思えてこないでしょうか.
基底ベクトルを反変基底を選んだときは,当然,その成分ベクトルは共変ベクトルになります.
Important
共変基底の成分ベクトルは反変的,反変基底の成分ベクトルは共変的.
| [¶] | 『成分ベクトルは反変ベクトルである』とだけ書いてある教科書がありますが,それは暗に共変基底を選んでいるからです.確かに,慣用的にメインで使う基底には共変基底(添字が右下にあるもの)を使うことが多いのですが,とにかく共変ベクトルと反変ベクトルの双対性を考えれば,そのような一方的な定義は混乱を招き,視野を狭めることになると思います. |
反変ベクトルの例2
もう一つの例として,座標系を 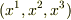 から
から 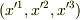 に変換する際の座標成分の微係数
に変換する際の座標成分の微係数 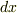 を考えてみます.微積分で勉強したチェーンルールを使って,微係数は次のように書けます.
を考えてみます.微積分で勉強したチェーンルールを使って,微係数は次のように書けます.
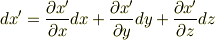
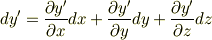
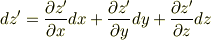
この変換公式をよく見ると,反変ベクトルの変換公式と同じですから,微係数を並べたベクトル 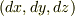 は反変ベクトルであることが分かります.
は反変ベクトルであることが分かります.
せっかく反変ベクトルなのですから,添字は右上に書くことにして  と名前を付け替えることにします.すると, まとめて次のように書けます.
と名前を付け替えることにします.すると, まとめて次のように書けます.
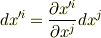
| [#] | 座標成分の微係数は 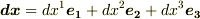 と書けますので,座標成分だからと言って先ほどの反変ベクトルの例1と何も変わりません.何となく頭がモヤモヤしてる人は,ここらで知識を整理してみて下さい.パソコンの画面を眺めているだけではダメですよ. と書けますので,座標成分だからと言って先ほどの反変ベクトルの例1と何も変わりません.何となく頭がモヤモヤしてる人は,ここらで知識を整理してみて下さい.パソコンの画面を眺めているだけではダメですよ. |
共変ベクトルの例
ベクトル 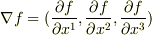 を考えます.
を考えます. 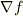 の座標変換は,次式に従います.微積分に出てきた,チェーンルールです
の座標変換は,次式に従います.微積分に出てきた,チェーンルールです
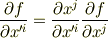
ここで 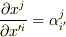 と置けば,
と置けば, 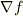 は共変ベクトルであることが分かります.関数
は共変ベクトルであることが分かります.関数 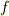 は,形式的に外してしまっても良いので, ∇は共変ベクトルだ ということが分かりました.(まだ
は,形式的に外してしまっても良いので, ∇は共変ベクトルだ ということが分かりました.(まだ  を習っていない人,ゴメンナサイ(>_<) )
を習っていない人,ゴメンナサイ(>_<) )
| [♠] | 座標変換の際,ベクトル 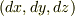 と と 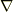 が違うタイプのベクトルだということで混乱する人がよくいます.この話題は 微分演算子の座標変換 で取り上げます.共変ベクトルと反変ベクトルが分かっている人にとって,微分演算子の座標変換は何にも難しくないでしょう. が違うタイプのベクトルだということで混乱する人がよくいます.この話題は 微分演算子の座標変換 で取り上げます.共変ベクトルと反変ベクトルが分かっている人にとって,微分演算子の座標変換は何にも難しくないでしょう. |