面積ベクトル
ある面積を持つ平面があるとき,この平面に垂直な方向(法線方向)に,長さがその面積に等しいベクトルを考え,これを 面積ベクトル と呼びます.
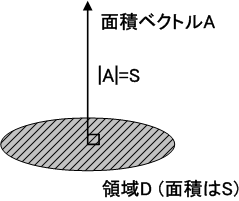
例えば,一定圧力の流体中に沈めた板は『板と垂直な方向に,(面積)  (圧力)の力』を受けますから,このような力を表現する際に面積ベクトルを使えば便利そうだということが分かるでしょう.
(圧力)の力』を受けますから,このような力を表現する際に面積ベクトルを使えば便利そうだということが分かるでしょう.
一般に曲面は平らではありませんが,曲面上の点とその点で定義される法線ベクトルを考え,その点を中心とする微小な面積を考えることで面積ベクトルの微分形を考えることもできます.(ただし,曲面は至るところ十分に滑らかだとします.)
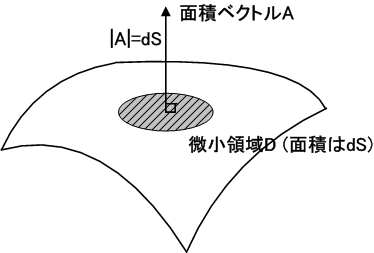
この考え方は,微小な面積はほぼ平らだと見られる,という微分法のアイデアに基づくものです.解析学的に細かいことは証明しませんが,曲面が連続で滑らかならば,このような見方は妥当なものです.
面積ベクトルの和
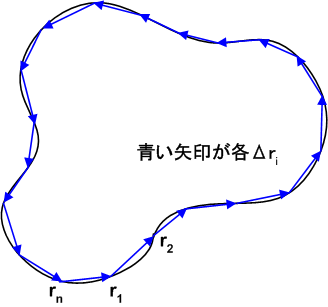
面積ベクトルの重要な性質として,『閉曲面に関して面積ベクトルの総和を取ると零になる』というものがあります.この性質を理解するために,まず平面上の閉曲線 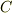 を考えます.曲線を
を考えます.曲線を  個の弧に分割し,各分割点の位置ベクトルを
個の弧に分割し,各分割点の位置ベクトルを 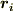 とします.そして,
とします.そして,  と置きます.(ただし,
と置きます.(ただし, 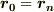 とします.)
とします.)
当然のことながら,一周していますので,ベクトル 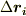 の総和は零になります.
の総和は零になります.
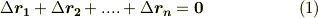
各 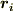 を時計回りに回転させることを考えましょう.ベクトルは行列
を時計回りに回転させることを考えましょう.ベクトルは行列 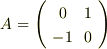 を左から掛けることで,時計回りに
を左から掛けることで,時計回りに  回転することが出来ます.
回転することが出来ます.
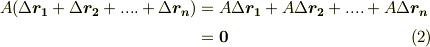
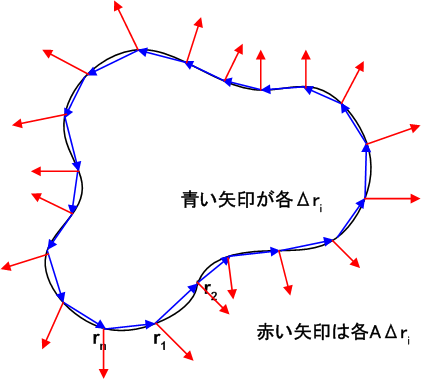
各 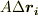 の大きさは,ほぼ
の大きさは,ほぼ 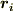 と
と 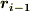 の間の曲線の長さ,
の間の曲線の長さ, 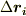 の向きは,ほぼ曲線の法線方向ですから,式
の向きは,ほぼ曲線の法線方向ですから,式 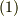 は,『面積ベクトルの和が零になる』ということを"ほぼ"表わしていると言えるでしょう.曲線の分割が有限な限り,各
は,『面積ベクトルの和が零になる』ということを"ほぼ"表わしていると言えるでしょう.曲線の分割が有限な限り,各 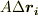 の長さや向きは少しいい加減なわけですが,
の長さや向きは少しいい加減なわけですが,  という極限を取れば,各
という極限を取れば,各  は『曲線の接線方向を向き,長さは曲線の微小要素
は『曲線の接線方向を向き,長さは曲線の微小要素  に等しいベクトル』となります.表現は積分形になります.
に等しいベクトル』となります.表現は積分形になります.  と表わすことにして,次の等式がなりたちます.
と表わすことにして,次の等式がなりたちます.

同様に,閉曲面で,全領域  に渡って面積ベクトル
に渡って面積ベクトル 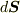 を積分すれば
を積分すれば 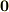 になります.
になります.

theorem
閉曲面の面積ベクトルの総和は 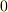 になります.
になります.
この結果は,実は次のような状況をイメージできれば,感覚としては当然の結果だと言えます.空気中に何か物を置くと,その物体は四方八方から空気圧を受けます.例えば,机の上にボールを置いた様子を想像してください.これぐらい物体が小さければ,空気圧は一定とみなせるので,これを 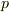 とします.ボール表面の微小面積が受ける力
とします.ボール表面の微小面積が受ける力 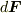 は,面積ベクトル
は,面積ベクトル 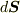 を用いて
を用いて 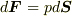 と表現できるでしょう.これを,ボールの表面積全体に渡って積分します.
と表現できるでしょう.これを,ボールの表面積全体に渡って積分します.
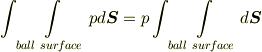
この右辺は 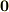 になるはずです.なぜかと言えば,もし右辺が
になるはずです.なぜかと言えば,もし右辺が 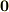 でなければ,ボールはどちらかから力を受け,独りでに転がり始めてしまうはずだからです.『ボールが勝手に動き出すはずない』という物理的経験則を,数学の証明にするのはかなり乱暴ですが,面積ベクトルの和が零になることの説明として,心の中でこんな物理的意味を考えておくと定理を忘れないと思います.
でなければ,ボールはどちらかから力を受け,独りでに転がり始めてしまうはずだからです.『ボールが勝手に動き出すはずない』という物理的経験則を,数学の証明にするのはかなり乱暴ですが,面積ベクトルの和が零になることの説明として,心の中でこんな物理的意味を考えておくと定理を忘れないと思います.
ささやかな応用
次のような高さ  ,底面が直角三角形の三角柱を考えます.
,底面が直角三角形の三角柱を考えます.

この三角柱について,面積ベクトルの総和を取ります.
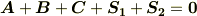
ここで,明らかに 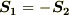 なので,
なので,  が成り立ちます.残りの項だけを考えます.
が成り立ちます.残りの項だけを考えます.
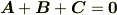
右辺に 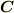 だけ移項し,両辺二乗します.
だけ移項し,両辺二乗します.
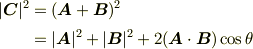
ここで 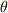 は
は 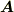 と
と 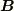 がなす角ですが,
がなす角ですが, 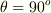 なので
なので  です.よって次式がなりたちます.
です.よって次式がなりたちます.

ピタゴラスの定理は確かに成り立っています.
| [*] | 実は,ベクトルの内積を使っている辺りで,この空間ではピタゴラスの定理に従う計量を使うことが暗黙の前提になっているため,この結果はピタゴラスの定理の「証明」にはなっていません.しかし,面積ベクトルの理解を深めるには,なんだか面白い結果だと思うのですが,みなさんはどう思いますか? |
練習問題
次図のような四面体を考えます.頂点  に集まる辺は,全て直角に交わっています.
に集まる辺は,全て直角に交わっています.
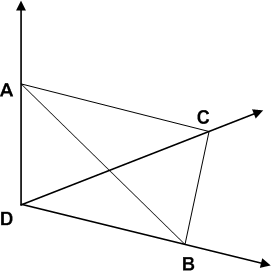
ここで  の面積を
の面積を  ,
,  の面積を
の面積を 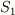 ,
, 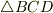 の面積を
の面積を 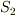 ,
, 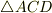 の面積を
の面積を 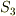 とするとき,各面積の間に次の関係式が成り立つことを示して下さい.(面積ベクトルの和が零になる関係から,全セクションの例と同様の計算で求められます.)
とするとき,各面積の間に次の関係式が成り立つことを示して下さい.(面積ベクトルの和が零になる関係から,全セクションの例と同様の計算で求められます.)
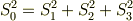
| [†] | この関係式は,著者が高校生のときに発見し,当時,嬉しくて四平方の定理と名づけた思い出のものです.著者以前にも絶対誰かが発見している関係式でしょうし,四平方の定理という名前の定理は既に他にあるらしいのですが,なんにせよ,自分で何か定理を導くのは嬉しいものです.この問題はピタゴラスの定理の三次元版になっていますが,そのまま四次元図形に拡張して 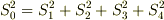 のような公式を導くのは簡単です.この場合,各 のような公式を導くのは簡単です.この場合,各 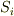 は体積になります. は体積になります. |