状態数Ωと分配関数Ｚの関係

この記事ではミクロカノニカル集合で扱われる状態数Ωと， カノニカル集合で扱われる分配関数の関係を求めます． その方法は，エントロピーＳを両方で求めて， イコールと置くだけです．

ミクロカノニカル集合(ΩとＳ)

これは有名なボルツマンの式です．

えいっ！

S = k_B \log \Omega \tag{1}

カノニカル集合(ＺとＳ)

これは少し考えないといけません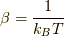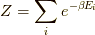．\beta = \dfrac{1}{k_B T} ， Z = \sum_i e^{- \beta E_i} として，

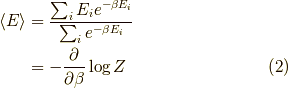
\langle E \rangle &= \dfrac{\sum_i E_i e^{- \beta E_i}}{\sum_i e^{- \beta E_i}} \\&= - \dfrac{\partial}{\partial \beta} \log Z \tag{2}

であり，

F = - \dfrac{1}{\beta} \log Z \tag{3}

でした．よって，

S = \dfrac{\langle E \rangle - F}{T} \tag{4}

を利用すればよく，

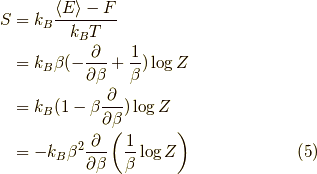
S &= k_B\dfrac{\langle E \rangle - F}{k_B T} \\&= k_B \beta ( - \dfrac{\partial}{\partial \beta} + \dfrac{1}{\beta}) \log Z \\&= k_B( 1 -\beta \dfrac{\partial}{\partial \beta}) \log Z \\&= - k_B \beta^2 \dfrac{\partial}{\partial \beta} \left( \dfrac{1}{\beta} \log Z \right) \tag{5}

となります．ここで，

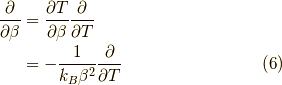
\dfrac{\partial}{\partial \beta} &= \dfrac{\partial T}{\partial \beta} \dfrac{\partial}{\partial T} \\&= -\dfrac{1}{k_B \beta^2} \dfrac{\partial}{\partial T} \tag{6}

を利用すれば，

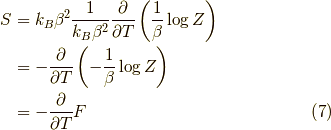
S &= k_B \beta^2 \dfrac{1}{k_B \beta^2} \dfrac{\partial}{\partial T} \left( \dfrac{1}{\beta} \log Z \right) \\&= - \dfrac{\partial}{\partial T} \left( - \dfrac{1}{\beta} \log Z \right) \\&= -\dfrac{\partial}{\partial T} F \tag{7}

なんだ，これは 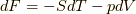dF = -SdT- pdV から求まる結果と一致しますね．つまり，

S = - \left( \dfrac{\partial F}{\partial T} \right)_V \tag{8}

です．

まとめ

これで，両手法でエントロピー 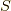S が求まりました．イコールで結びましょう！！

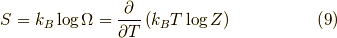
S = k_B \log \Omega = \dfrac{\partial}{\partial T} \left( k_B T \log Z \right) \tag{9}

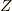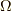これが，求めたかった Z と \Omega の関係です． 込み入った計算の結果の割には美しいと思います． それでは，今回はこの辺で，お疲れ様でした．