ヤングの干渉実験2
ヤングの干渉実験1では,実験の内容と,明線条件・暗線条件について学びました.ここでは,実際に行路差を計算し,さらに詳しく実験を見ていきます.
行路差の計算
ヤングの干渉実験の装置は,以下のようになっていました.
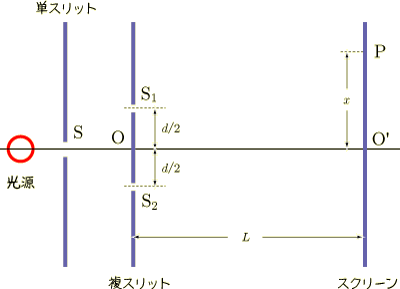
ここで, 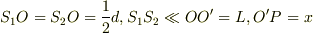 とします.
とします.
では,実際に行路差を計算しましょう.三平方の定理から,
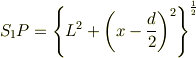
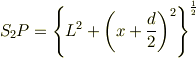
と分かります.したがって,
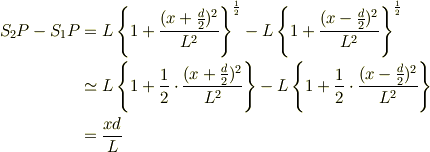
と求まります( 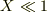 のときに成り立つ
のときに成り立つ 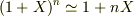 という近似式を使っています).
という近似式を使っています).
ヤングの干渉実験1では,実験の内容と,明線条件・暗線条件について学びました.ここでは,実際に行路差を計算し,さらに詳しく実験を見ていきます.
ヤングの干渉実験の装置は,以下のようになっていました.

ここで, 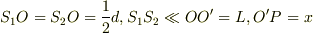 とします.
とします.
では,実際に行路差を計算しましょう.三平方の定理から,
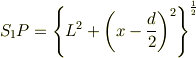
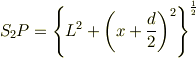
と分かります.したがって,
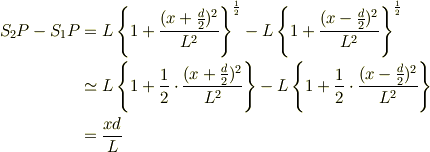
と求まります( 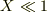 のときに成り立つ
のときに成り立つ 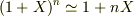 という近似式を使っています).
という近似式を使っています).