無限の井戸型ポテンシャル

home > 量子力学 >

[サイトマップ]

1次元シュレーディンガー方程式の典型的な問題である無限井戸型ポテンシャルを解きます．このページは長くなったのでPDF版も置いておきます．

無限の井戸型ポテンシャル [PDF]

ポテンシャルの形

1次元無限井戸型ポテンシャルのシュレーディンガー方程式を解いて，粒子がどのような分布をとるのかを見てみます．つぎの式で表されるポテンシャルを無限の井戸型ポテンシャルと呼びます．

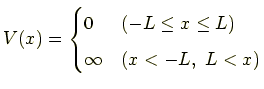$\displaystyle V(x)=\begin{cases}0 & (-L < x < L) \\ \infty & (x \ge -L,~ L \le x) \end{cases}$ (1)

このポテンシャルを図に描くとつぎのようになります．

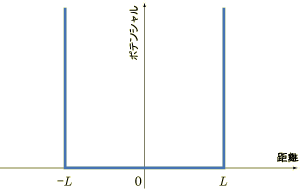
-L から L の間でポテンシャルはゼロ，それより外側ではポテンシャルが無限に高いので粒子は外に出ることができません．外に出られないことから，箱型ポテンシャルとも呼ばれます．

シュレーディンガー方程式の書きだし

一次元のシュレーディンガー方程式，すぐ思い浮かぶでしょうか．これです．

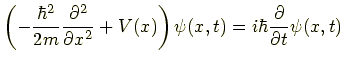$\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + V(x)\right)\psi(x,t) = i\hbar \frac{\partial}{\partial t}\psi(x,t)$ (2)

これは偏微分方程式なので，変数分離して解いていきます．

変数分離

変数分離するため

$\displaystyle \psi(x,t)=f(x)g(t)$

を解として式(2)の ψ(x,t) に代入するのがお決まりの方法です．

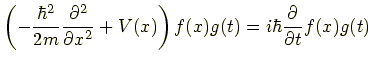
$\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right)f(x)g(t) =i\hbar \frac{\partial}{\partial t}f(x)g(t)$

左辺の括弧を展開します．

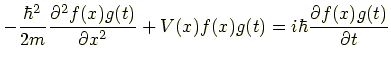
$\displaystyle -\frac{\hbar^2}{2m}\frac{\partial^2f(x)g(t)}{\partial x^2}+V(x)f(x)g(t) =i\hbar\frac{\partial f(x)g(t)}{\partial t}$

左辺第1項は x の偏微分なので， t の関数である g(t) は偏微分と関係ないから前に出します．

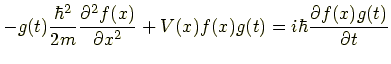
$\displaystyle -g(t)\frac{\hbar^2}{2m}\frac{\partial^2f(x)}{\partial x^2}+V(x)f(x)g(t) =i\hbar \frac{\partial f(x)g(t)}{\partial t}$

同様に右辺の f(x) も前に出します．

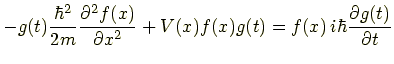
$\displaystyle -g(t)\frac{\hbar^2}{2m}\frac{\partial^2f(x)}{\partial x^2}+V(x)f(x)g(t) =f(x)\,i\hbar \frac{\partial g(t)}{\partial t}$

変数分離形にするため，両辺を f(x)g(t) で割ります．

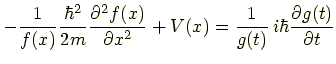
$\displaystyle -\frac{1}{f(x)}\frac{\hbar^2}{2m}\frac{\partial^2f(x)}{\partial x^2}+V(x) =\frac{1}{g(x)}\,i\hbar \frac{\partial g(t)}{\partial t}$

これで左辺は x，右辺は t という具合に変数が分離できました．

ところで，異なる変数の関数が含まれた式の両辺が「イコールで結ばれている」ことに注目してください．変数が両辺で違うということは，それぞれ好き勝手な値を取れるということです．にもかかわらずイコールで結ばれているのは，両辺とも定数であるに違いないということです．この定数を E とおきます．

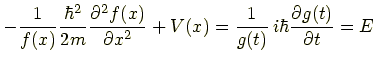
$\displaystyle -\frac{1}{f(x)}\frac{\hbar^2}{2m}\frac{\partial^2f(x)}{\partial x^2}+V(x) =\frac{1}{g(x)}\,i\hbar \frac{\partial g(t)}{\partial t} =E$

したがって

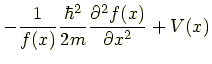
$\displaystyle -\frac{1}{f(x)}\frac{\hbar^2}{2m}\frac{\partial^2f(x)}{\partial x^2}+V(x)$	$\displaystyle = E$
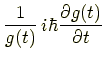
$\displaystyle \frac{1}{g(x)}\,i\hbar \frac{\partial g(t)}{\partial t}$	$\displaystyle = E$

整理すると

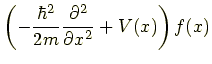
$\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + V(x)\right)f(x)$	$\displaystyle = Ef(x)$ (3)
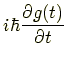
$\displaystyle i\hbar \frac{\partial g(t)}{\partial t}$	$\displaystyle = Eg(t)$ (4)

それぞれ一変数しか持たない常微分方程式になりました．特に式(3)は時間 t を含まないため，定常状態のシュレーディンガー方程式と呼ばれます．以下では時間発展を考えず，定常状態を考えます．

定常状態のシュレーディンガー方程式

式(3)の f(x) は定常状態のシュレーディンガー方程式の解であり，定常状態の波動関数です．これをいまから求めて行きます．ポテンシャル V(x) は

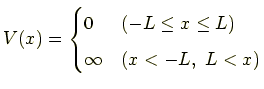
$\displaystyle V(x)=\begin{cases}0 & (-L < x < L) \\ \infty & (x \ge -L,~ L \le x) \end{cases}$

で定義されてましたから，V(x) = 0 の場合は

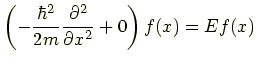
$\displaystyle \left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + 0\right)f(x) = Ef(x)$

つまり

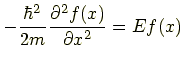
$\displaystyle -\frac{\hbar^2}{2m} \frac{\partial^2f(x)}{\partial x^2}=Ef(x)$

となることがすぐに分かります．しかし V(x) = ∞ の場合は

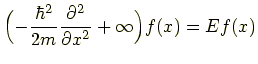
$\displaystyle \Bigl(-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \infty \Bigr) f(x) = Ef(x)$

となってよく分かりませんよね．こんなときは物理的な意味を考えます．この x < -L, L < x という場合はどんな場合だったでしょうか．ポテンシャルが無限大の場合です．ということは，粒子はポテンシャルの壁を超えられません．つまり x < -L, L < x の場所には粒子は行けないのです．シュレーディンガー方程式はそもそも粒子の存在確率を表すための式なので，粒子が存在しない場所で解はゼロになるはずです．ですから V(x) = ∞ の場合は

$\displaystyle f(x)=0$

だと考えます．したがって

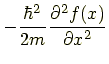
$\displaystyle -\frac{\hbar^2}{2m} \frac{\partial^2f(x)}{\partial x^2}$	$\displaystyle = Ef(x) ,\quad (-L \le x \le L)$ (5)
$\displaystyle f(x)$	$\displaystyle = 0 ,\quad (x > -L,~ L < x)$ (6)

の2つの場合に分けられます．式(6)はもうこれでいいので，式(5)を解きます．変形すると

$\displaystyle \frac{\partial^2f(x)}{\partial x^2}=-\frac{2mE}{\hbar^2}f(x)$

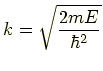ここで $\displaystyle k=\sqrt{\frac{2mE}{\hbar^2}}$ とおくと，

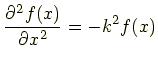
$\displaystyle \frac{\partial^2f(x)}{\partial x^2}=-k^2f(x)$

となり，これに解として

$\displaystyle f(x)=e^{\alpha x}$

を代入すると

$% latex2html id marker 510 $\displaystyle (\alpha ^2 + k^2)=0 \quad \therefore\ \alpha=\pm ik$$

よって特解は

$\displaystyle e^{ikx} ,\quad e^{-ikx}$

一般解はこの線型結合で書けて

$\displaystyle f(x)$	$\displaystyle =Ae^{ikx}+Be^{-ikx}$
	$\displaystyle =A\{\cos(kx)+i\sin(kx)\}+B\{\cos(kx)-i\sin(kx)\}$
	$\displaystyle =(A+B)\cos(kx)+i(A-B)\sin(kx)$

ここで1行目から2行目のところでオイラーの公式を使っています．定数 A+B，i(A-B) を新たに A，B とおくと

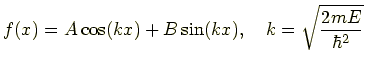$\displaystyle f(x) = A\cos (kx) + B \sin (kx) ,\quad k=\sqrt{\frac{2mE}{\hbar^2}}$ (7)

となります．井戸型ポテンシャルを考えることで，とりあえず

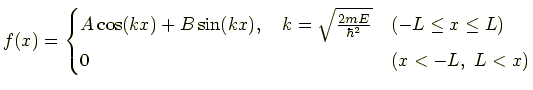$\displaystyle f(x)= \begin{cases}A\cos(kx)+B\sin (kx) , \quad k=\sqrt{\frac{2mE}{\hbar^2}} & (-L\le x \le L)\\ 0 & (x>-L,\ L<x) \end{cases}$ (8)

というところまで分かりました．つぎに境界条件と規格化条件を考えます．

境界条件

ポテンシャル V(x) は式(1)で与えられています． V(x) は x が -L より小さくなる場所， L より大きくなる場所からそれぞれ無限大になります．さきほど考えたように，ポテンシャルが無限大の場所では粒子が存在できません． x = -L と x = L の場所で f(x) = 0 です．シュレーディンガー方程式の解は連続でなければいけないので，式(8)もこの条件を満たさないといけません．これが境界条件です．したがって

$\displaystyle f(-L)$	$\displaystyle =A\cos(-kL)+B\sin(-kL)=0$
$\displaystyle f(L)$	$\displaystyle =A\cos(kL)+B\sin(kL)=0$

cos(-x) = cos(x)，sin(-x) = -sin(x) という関係を使うと

$\displaystyle A\cos(kL)-B\sin(kL)=0$ (9)
$\displaystyle A\cos(kL)+B\sin(kL)=0$ (10)

上式から A，B の値が決まります．まず A = B = 0 という場合が考えられますが，この場合 f(x) = 0 となって無意味なので考えません．

A = 0 の場合を考えます．式(9)と(10)の辺々を引くと

$\displaystyle 2B\sin(kL)=0$

A と B は両方一緒にはゼロにならないので B ≠ 0 ですから

$\displaystyle \sin(kL)=0$

したがって

$\displaystyle kL = n\frac{\pi}{2} ,\quad (n=2,4,6,\cdots)$

つぎは B = 0 の場合です．式(9)，(10)の辺々を足すと

$\displaystyle 2A\cos(kL)=0$

A と B は両方一緒にはゼロにならないので A ≠ 0 ですから

$\displaystyle \cos(kL)=0$

したがって

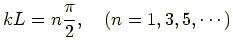
$\displaystyle kL = n\frac{\pi}{2} ,\quad (n=1,3,5,\cdots)$

以上の場合をまとめると

$\displaystyle k = n\frac{\pi}{2L} ,\qquad (n=1,2,3,\cdots)$ (11)

となります．k は連続な値ではなく，ある n に対して許される値が決まってしまいました． π/2L の n 倍になっます．飛び飛びなんです．この飛び飛びの状態を量子化されているといい，整数 n は量子数と呼ばれます．

規格化条件

式(11)で k の値が決まったので，これを式(8)に代入すると

$\displaystyle f_n(x)= \begin{cases}\displaystyle A\cos\left(\frac{n\pi}{2L}x\ri... ...\quad (n=1,2,3,\cdots) & (-L\le x \le L)\\ [1.2em] 0 & (x>-L,\ L<x) \end{cases}$

です．さらに，いままで調べたように，n が偶数（A = 0 の場合）ならサイン関数， n が奇数（B = 0 の場合）ならコサイン関数になります．すなわち

$\displaystyle f_n(x)= \begin{cases}\displaystyle A\cos\left(\frac{n\pi}{2L}x\ri... ...right) ,\quad (n=偶数) & (-L\le x \le L)\\ [1.2em] 0 & (x>-L,\ L<x) \end{cases}$

というところまで分かりました．ここで規格化条件から係数 A，B を求めます．波動関数を規格化するには，全区間で波動関数の絶対値の2乗を積分して 1 になるようにすればよかったので

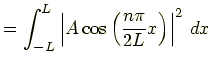
$\displaystyle 1$	$\displaystyle =\int_{-L}^{L}\left\vert A\cos\left(\frac{n\pi}{2L}x\right)\right\vert^2\,dx$
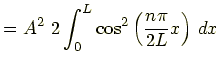
	$\displaystyle =A^2\ 2\int_0^{L}\cos^2\left(2\cdot \frac{n\pi}{2L}x\right)\,dx$
	$\displaystyle =2A^2\int_0^{L}\frac{1+\cos\left(\frac{n\pi}{L}x\right)}{2}\,dx$
	$\displaystyle =2A^2\left[\frac{x}{2}+\frac{L}{2n\pi}\sin\left(\frac{n\pi}{L}x\right)\right]_0^L$
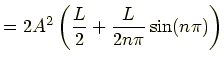
	$\displaystyle =2A^2\left(\frac{L}{2}+\frac{L}{2n\pi}\sin(n\pi)\right)$
	$\displaystyle =A^2L$
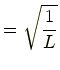
$% latex2html id marker 554 $\displaystyle \therefore \quad A$$	$\displaystyle =\sqrt{\frac{1}{L}}$

同様に計算して

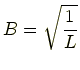
$\displaystyle B=\sqrt{\frac{1}{L}}$

したがって

$\displaystyle f_n(x)= \begin{cases}\displaystyle \sqrt{\frac{1}{L}}\cos\left(n\... ...right) ,\quad (n=偶数) & (-L\le x \le L)\\ [1.2em] 0 & (x>-L,\ L<x) \end{cases}$ (12)

となり，定常状態の波動関数が求まりました．

エネルギー固有値

定常状態のシュレーディンガー方程式のエネルギー固有値は，なにを隠そう変数分離のときの定数 E に他なりません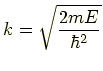． $\displaystyle k=\sqrt{\frac{2mE}{\hbar^2}}$ でしたから，式(11)より

$\displaystyle \sqrt{\frac{2mE}{\hbar^2}} = n\frac{\pi}{2L} ,\quad (n=1,2,3,\cdots)$ (13)

したがって n に対応するエネルギー固有値 E_n は

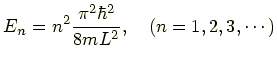$\displaystyle E_n = n^2\frac{\pi^2 \hbar^2}{2mL^2} ,\quad (n=1,2,3,\cdots)$ (14)

となります．

零点エネルギー

エネルギー固有値 E_n の n が一番小さいとき，すなわち n = 1 のときでもエネルギーの最低値はゼロになりません． $\pi^2\hbar^2/8mL^2$ という有限の値をとります．ということは，井戸型ポテンシャル中の粒子はエネルギーがゼロになることを許されないのです．たとえ絶対零度になっても粒子は振動していて，エネルギーをもっています．このエネルギーを零点エネルギーといいます．古典力学では絶対零度ですべての粒子は静止しているはずですが，量子力学ではそうはならないのです．不思議ですね．

[home] [量子力学] [ページの先頭]