任意方向の1/2スピンの回転と実現方法
この記事は有名サイト『EMANの物理学』さんの スピノールの記事 に感銘を受け書いた記事です.
理論的な内容はあまりなく,EMANさんの理論が上手くできていると言うことを確認する感じです.
任意方向軸  のスピンの有限角度
のスピンの有限角度  回転を
扱います.ちなみにこの場合の
回転を
扱います.ちなみにこの場合の  の正の方向は,その方向に右ねじを回して進む方向が,
の正の方向は,その方向に右ねじを回して進む方向が, 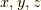 軸の正の方向と一致するように決めます.(2020.6.14追記:回転演算子がなぜこれでいいのか, 証明した記事 を作りました.)
軸の正の方向と一致するように決めます.(2020.6.14追記:回転演算子がなぜこれでいいのか, 証明した記事 を作りました.)
EMANさんの結果
EMANさんの記事では,一般方向の有限角回転の演算子が書いてあります. それは,結果を要約して示すと,

ここで,  は2×2のユニタリー行列,
は2×2のユニタリー行列,

は,長さ  が回転角であり,向き
が回転角であり,向き 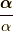 が回転軸となるベクトル,シグマはパウリ行列であり,
が回転軸となるベクトル,シグマはパウリ行列であり,
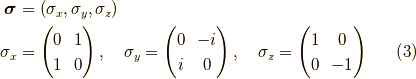
なので,内積は2×2行列であり,

となります.
EMANさんの記事には, 軸方向の回転行列
軸方向の回転行列  が書いてあります.
それは,
が書いてあります.
それは,  ,
, 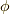 :任意の時であり,
:任意の時であり,
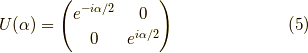
これを包含する回転行列 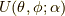 を作るのがこの記事です.
を作るのがこの記事です.
望む計算の実行
ここで,一つ準備をします.

つまり,  の二乗は単位行列です.
後は,式
の二乗は単位行列です.
後は,式 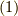 の計算を具体的に実行するのみで,
結果は,
の計算を具体的に実行するのみで,
結果は,
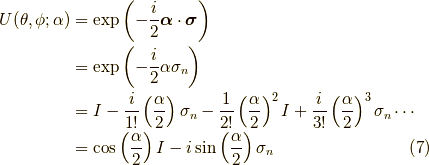
つまり,  方向を向いたスピノール
方向を向いたスピノール
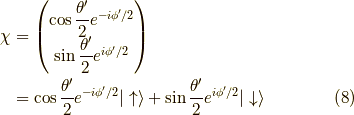
を回転軸  として,角度
として,角度  だけ回転する時には,回転後のスピノールを
だけ回転する時には,回転後のスピノールを  として,次のような計算をします.
として,次のような計算をします.
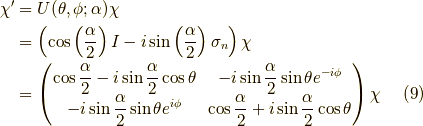
具体例の計算(EMANさんの結果)
ここできちんとEMANさんの結果,式 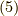 と一致することを確認します.
それは
と一致することを確認します.
それは  ,
,  :任意でしたから,
:任意でしたから,
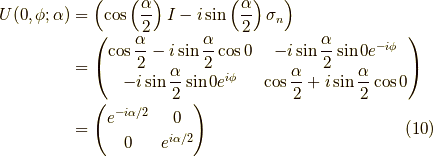
OKです.一致しました.
具体例の計算(変化しないはずの回転の結果)
また,  の固有ベクトル(スピノール)が,上記の
の固有ベクトル(スピノール)が,上記の  で,その固有値は
で,その固有値は  です
から,
です
から,  かつ
かつ  の時
の時  と書くと,
と書くと, 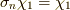 ですから,
ですから,
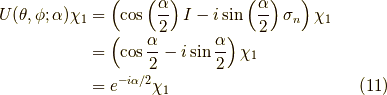
なるほど,回転軸の方を向いたスピノール 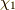 の回転では,
変化しないはずだと思いましたが,回転角
の回転では,
変化しないはずだと思いましたが,回転角  の大きさに依存して,
全体の位相が変わっていくようです.
の大きさに依存して,
全体の位相が変わっていくようです.
具体例の計算(アダマールゲート)
以前,量子コンピュータ関連の講義を聞いた時に, アダマールゲートというものを習いました. それは,
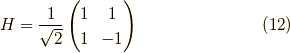
であり,  に相当する回転なのだそうです.
に相当する回転なのだそうです.
では,これは 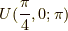 で再現できるでしょうか?
で再現できるでしょうか?
計算してみると,
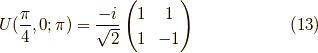
全体の位相 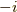 を除いて一致しました.
実はこれを再現したくて今回の計算を始めたのです.
を除いて一致しました.
実はこれを再現したくて今回の計算を始めたのです.
実際に回転ってどうやるの?
さて,今回はスピンの回転でしたが,実際に回転して見ろと言われても,
はて?どうしたものか?と言う方もいらっしゃることと思います.
実は,磁場 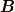 を掛けると回転できます.
を掛けると回転できます.
磁場 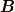 とスピン
とスピン 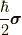 の結合を表すハミルトニアン
の結合を表すハミルトニアン  は,
2×2行列となり,
は,
2×2行列となり,
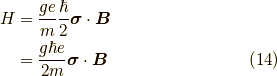
ここで, 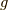 はランデのg因子と言い,およそ大きさが2くらいの無次元数です.
系の時間発展は,波動関数(スピノール)を
はランデのg因子と言い,およそ大きさが2くらいの無次元数です.
系の時間発展は,波動関数(スピノール)を 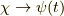 と書き換えて(つまり二行一列の行列),
と書き換えて(つまり二行一列の行列),

式  の二行目と比較して,
の二行目と比較して,
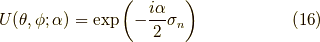
でしたから,一秒間に 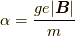 ラジアンずつ回転すると分かります.
良く言われることですが
ラジアンずつ回転すると分かります.
良く言われることですが 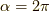 の回転でスピノールは元に戻らず,
位相因子
の回転でスピノールは元に戻らず,
位相因子 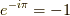 が掛かるのが,式
が掛かるのが,式 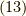 の二乗の結果からも分かります.
の二乗の結果からも分かります.
それでは今日はこの辺で.お疲れ様でした.