任意の方向を向いたスピンのxyz方向固有状態での展開
この記事は, スピン一重項と三重項のxy方向固有状態での展開 という記事の姉妹編です.どちらを先に読んでも構いません. ちなみにこの記事は,J.J.サクライの「現代の量子力学」を意識して 書いてあります.
パウリ行列
まず,天下り的ですが,パウリ行列を次の様に定めます.




スピノール
スピンの状態は,二成分のスピノール [*] (ケット)
| [*] | スピノールといっても,計算は普通の行列と変わらないので安心してください. |

また,その共役転置(ブラ),

で表わされます.共役転置なので,虚数成分にはマイナスがつくことに注意してください.
スピンの方向 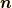 を次のようにオイラー角で定めます.
を次のようにオイラー角で定めます.
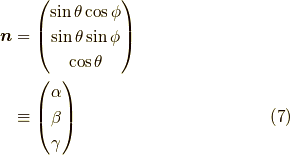
今,任意の方向 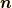 を向いたスピンは,
固有値を
を向いたスピンは,
固有値を 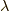 として,固有スピノール
として,固有スピノール 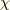

で表わされます.
つまり,
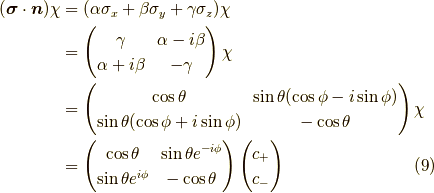
より, 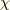 は,
は,
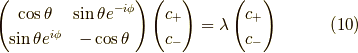
と求められます.
この固有値問題を解くと,
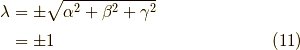
ですから, 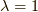 に対して,
に対して,
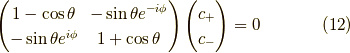
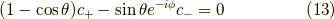
より,この固有スピノール( 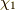 とする.)は,規格化因子を
とする.)は,規格化因子を 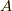 として,
として,
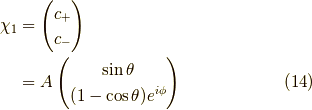
なので,規格化因子 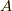 を求めると,
を求めると,
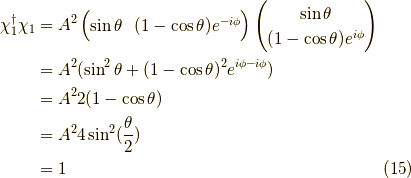
よって,

ここで, 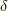 は任意の実数で位相因子と言います.
よって,
は任意の実数で位相因子と言います.
よって, 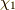 が求まりました.
が求まりました.
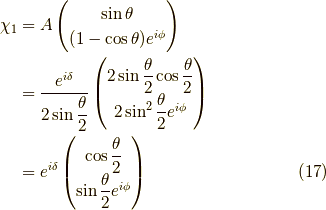
ここで, 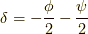 と置くと,
と置くと,
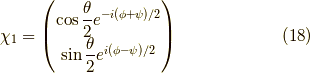
同様に, 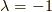 の時の固有スピノールは,
の時の固有スピノールは,
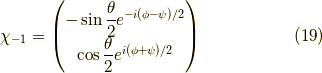
となります.
スピンの向きの期待値
いままで求めてきた,固有スピノールが本当に任意の方向を向いてるか, 確認してみましょう.
まず,z方向の成分の期待値を求めてみます.  について,
について,
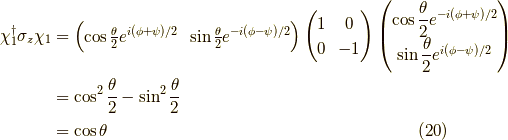
次にx成分です.
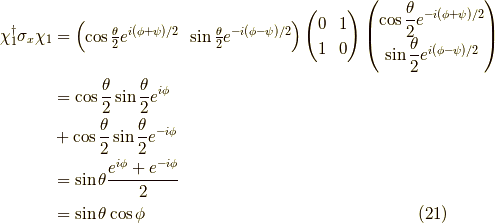
同様にして計算は省略しますが,y成分も同様に,
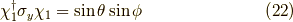
よって,確かに期待値としては,スピンはオイラー角で表わされる方向を向いていることが,
分かりました.z方向成分を観測する(磁場をかけてやる:シュテルン・ゲルラッハの実験)
と,確率 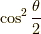 で,z軸正方向を,
確率
で,z軸正方向を,
確率 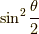 でz軸負方向を向くことが分かります.
でz軸負方向を向くことが分かります.
それでは,x方向成分を観測すると,どんな確率でx軸正方向とx軸負方向を向くのでしょうか?
それには,ちょっと工夫が必要です.どの軸方向でも原理は同じですから,
x軸とスピンのなす角を  と置くのです.
すると,
と置くのです.
すると,
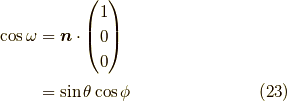
より,x軸の正の方向を向く確率は,
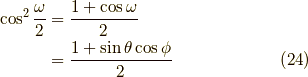
負の方向を向く確率は,
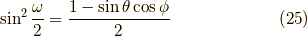
と成ります.
この結果は,式 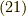 ,
,
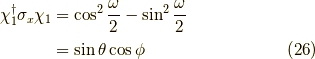
というx軸方向の期待値と一致し,つじつまがあっていることが分かります.
最後にy方向について書いておくと,y軸の正の方向を向く確率は,
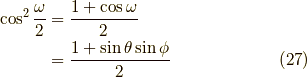
負の方向を向く確率は,
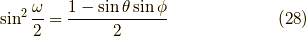
と成ります.
ちなみに,パウリ行列を 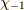 で挟んでやると,
で挟んでやると,
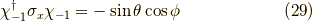
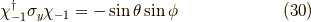
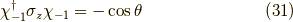
となり, 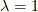 の時とは逆の方向を向いていることが分かります.
の時とは逆の方向を向いていることが分かります.
z方向の固有スピノール
ここで話の進む向きを変えて,z方向のスピノールについて考えます.
今考えてきた二成分のスピノールは,実はz方向の固有関数 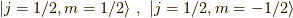 で展開してきたことにあたります.
で展開してきたことにあたります.
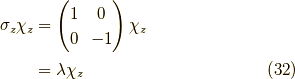
の固有スピノール,
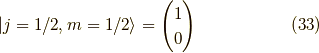
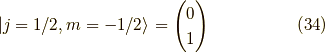
つまり,z方向での展開であることを明示すると,
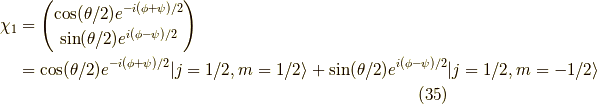
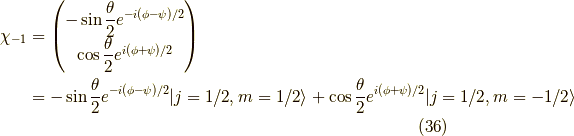
です.これをx方向での固有スピノールで展開してみましょう. x方向の固有スピノールは,
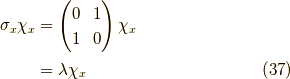
の固有状態ですから, 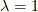 の時,
の時,
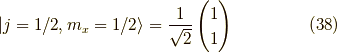
同様に 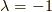 の時,
の時,
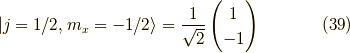
ですので,x方向のスピノールを
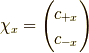
と置くと,
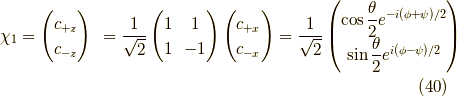
より,
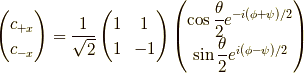
ただ冗長になるだけなので,最後の展開はしません.
ここで,特別な場合を考えてみましょう. 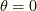 の時,
の時, 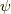 が任意なので,
が任意なので, 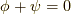 と置けて,
と置けて,
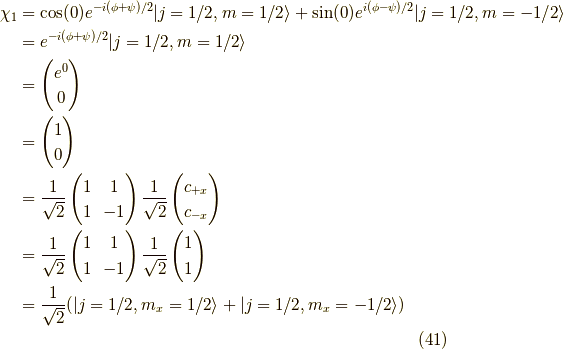
と,こういう風にz軸を向いているスピンは,
x方向で見ると,角運動量ベクトルがx軸の正方向の状態と,
負方向の状態が同じ重みで重ね合わさっていることが分かりましたね. 姉妹編 で見た,三重項の内の 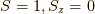 と同じような結果になりました.
これも古典論でのイメージができない状態です.
と同じような結果になりました.
これも古典論でのイメージができない状態です.
それでは,今日はここまで. お疲れ様でした.