フェルミオンの遅延グリーン関数の満たす式
少しあいまいな点もあり,自信がありませんが,「物性論で遅延グリーン関数を扱うけど なんでグリーン関数と言えるのか?」という疑問に答えたいと思います.
フェルミオンの遅延グリーン関数 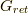 とは,greaterグリーン関数
とは,greaterグリーン関数 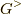 ,
lesserグリーン関数
,
lesserグリーン関数 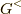 そしてシータ関数(階段関数とも)
そしてシータ関数(階段関数とも) 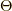 を用いて,
を用いて,
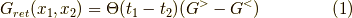
と表されます.ここで,greater,lesser関数は,それぞれ,場の演算子 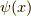 を用いて,
を用いて,
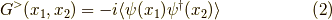
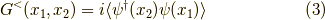
となります.よって,
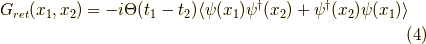
となります.場の演算子の時間発展は, 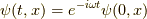 のように変化するので,結局式
のように変化するので,結局式 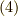 は,
は,
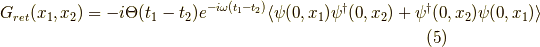
これで,時間依存性があらわになりました.
では,時間微分を計算してみましょう.
交換関係は 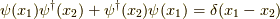 ですから,
括弧式の平均を取ると,自信はありませんが,どうやら
ですから,
括弧式の平均を取ると,自信はありませんが,どうやら 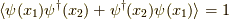 になるようです.(もしかしたら
になるようです.(もしかしたら 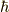 の何乗かが掛かったりするかもしれません. )
の何乗かが掛かったりするかもしれません. )
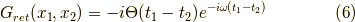
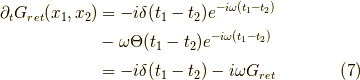
なお, 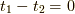 でのみ値を持つδ関数を含む項に対しては,
でのみ値を持つδ関数を含む項に対しては, 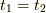 と置きました.
これは,少し変形してやれば,シュレーディンガー方程式に対するグリーン関数になっているようです.つまり,
と置きました.
これは,少し変形してやれば,シュレーディンガー方程式に対するグリーン関数になっているようです.つまり,
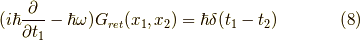
なんというか,右辺の 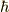 が気になりますが,
これなら,確かにグリーン関数とは呼べなくもないですね.
が気になりますが,
これなら,確かにグリーン関数とは呼べなくもないですね.
それでは,今日はこの辺で.お疲れさまでした.