相互作用表示

時間順序積(time-ordered product，T-productとも言う．)の計算は， どうやってすればいいのという方むけです．逐次近似の三次の項まで， 計算してみることにします．

前の記事は， シュレーディンガー表示とハイゼンベルク表示 次の記事は， 時間順序積

相互作用表示

シュレーディンガー表示では，状態ベクトルが時間発展をし， ハイゼンベルク表示では，演算子が時間発展をしましたね． ここで，相互作用表示という，時間発展のある部分を状態ベクトルがあらわし， 時間発展のまたある部分は演算子が受け持つ表示について考えます．

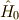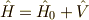ハミルトニアン \hat{H}_0 が，うまく解けるときを考えます． ここで \hat{H}=\hat{H}_0+\hat{V} という形のハミルトニアン をもつ系を考えます．

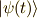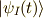シュレーディンガー表示の状態ベクトル |\psi(t)\rangle に対して， 相互表示作用での状態ベクトル | \psi_I (t) \rangle は次のようになります．

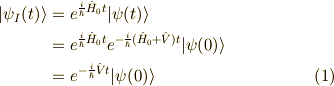
| \psi_I (t) \rangle &=e^{\frac{i}{\hbar}\hat{H}_0 t}|\psi(t)\rangle \\&= e^{\frac{i}{\hbar}\hat{H}_0 t}e^{-\frac{i}{\hbar}(\hat{H}_0 + \hat{V} ) t}|\psi(0)\rangle \\&= e^{-\frac{i}{\hbar} \hat{V} t}|\psi(0)\rangle \tag{1}

これをみると 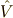\hat{V} が状態ベクトルの時間発展を表しているとわかりますね．

よって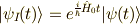， | \psi_I (t) \rangle &=e^{\frac{i}{\hbar}\hat{H}_0 t}|\psi(t)\rangle を逆に解いた，

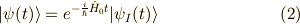
|\psi(t)\rangle &=e^{-\frac{i}{\hbar}\hat{H}_0 t}| \psi_I(t) \rangle \tag{2}

をシュレーディンガー方程式に代入します． シュレーディンガー方程式は

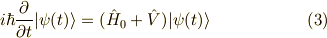
i\hbar\frac{\partial}{\partial t}| \psi (t) \rangle = (\hat{H}_0 + \hat{V}) | \psi(t) \rangle \tag{3}

でしたので代入すると，

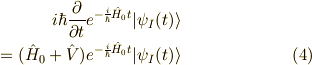
i\hbar\frac{\partial}{\partial t}e^{-\frac{i}{\hbar}\hat{H}_0 t}| \psi_I(t) \rangle \\= (\hat{H}_0 + \hat{V}) e^{-\frac{i}{\hbar}\hat{H}_0 t}| \psi_I(t) \rangle \tag{4}

変形して，

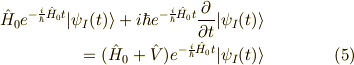
\hat{H}_0 e^{-\frac{i}{\hbar}\hat{H}_0 t} | \psi_I(t) \rangle + i\hbar e^{-\frac{i}{\hbar}\hat{H}_0 t}\frac{\partial}{\partial t} | \psi_I(t) \rangle \\= (\hat{H}_0 + \hat{V}) e^{-\frac{i}{\hbar}\hat{H}_0 t}| \psi_I(t) \rangle \tag{5}

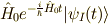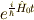両辺から \hat{H}_0 e^{-\frac{i}{\hbar}\hat{H}_0 t} | \psi_I(t) \rangle を引き，左から e^{\frac{i}{\hbar}\hat{H}_0 t} を掛けてやると，

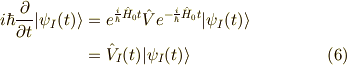
i\hbar \frac{\partial}{\partial t}| \psi_I (t) \rangle &= e^{\frac{i}{\hbar}\hat{H}_0 t} \hat{V} e^{-\frac{i}{\hbar}\hat{H}_0 t}| \psi_I(t) \rangle \\&= \hat{V}_I(t) | \psi_I(t) \rangle \tag{6}

となります．

ところで，今の話に出てきた 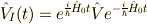\hat{V}_I(t)=e^{\frac{i}{\hbar}\hat{H}_0 t} \hat{V} e^{-\frac{i}{\hbar}\hat{H}_0 t} は， 運動方程式

\frac{d}{dt}\hat{V}_I(t)=\frac{i}{\hbar}[\hat{H}_0,\hat{V}_I(t)] \tag{7}

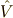に従います． \hat{V} の時間依存性は，ハミルトニアンの解ける部分 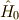\hat{H}_0 に依存しています．

一方で，状態ベクトルの時間発展式は ，式(6)の両辺を積分することにより，逐次的に求められます．

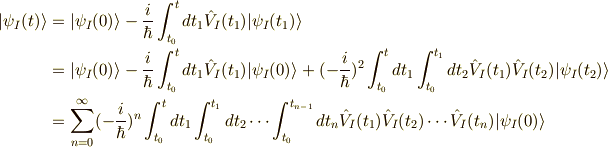
|\psi_I(t)\rangle &= |\psi_I(0)\rangle-\frac{i}{\hbar}\int_{t_0}^t dt_1 \hat{V}_I(t_1)| \psi_I (t_1) \rangle \\&= |\psi_I(0)\rangle-\frac{i}{\hbar}\int_{t_0}^t dt_1 \hat{V}_I(t_1)| \psi_I (0) \rangle+(-\frac{i}{\hbar})^2 \int_{t_0}^t dt_1 \int_{t_0}^{t_1} dt_2 \hat{V}_I(t_1)\hat{V}_I(t_2)| \psi_I (t_2) \rangle \\&= \sum^\infty_{n=0} (-\frac{i}{\hbar})^n \int_{t_0}^t dt_1 \int_{t_0}^{t_1} dt_2 \cdots \int_{t_0}^{t_{n-1}}dt_n\hat{V}_I(t_1)\hat{V}_I(t_2) \cdots \hat{V}_I(t_n)|\psi_I(0)\rangle

さて，次はいよいよ時間順序積の出番です．続きは こちら