クラインゴルドン演算子のグリーン関数

この記事では，相対論的量子力学（西島和彦著）に出てくるクラインゴルドン方程式についてグリーン関数を導きます．

この本に於いて，グリーン関数はいきなり出てきます．グリーン関数の知識は常識の様なので，その辺の事情を確認の意味で辿ってみれば，何かの役に立つと思い，ここに書きます．

クラインゴルドン方程式

クラインゴルドン方程式とは以下の様な式です．

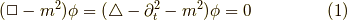
(\Box - m^2)\phi = (\triangle - \partial_t^2 -m^2)\phi = 0 \tag{1}

ここで \Box はダランベルシアンと言い，ラプラシアンと時間の二階微分から成ります．

この本同様にグリーン関数（遅延グリーン関数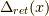） \Delta_{ret}(x) を先に示しておくと，

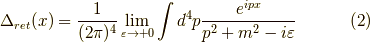
\Delta_{ret}(x) = \dfrac{1}{(2 \pi)^4} \lim_{\varepsilon \to +0} \int d^4p \dfrac{e^{ipx}}{p^2 + m^2 - i \varepsilon} \tag{2}
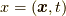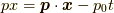の様になります．ここで， x = (\bm{x},t) であり， px = \bm{p}\cdot\bm{x}-p_0 t であり，
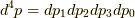d^4p = dp_1 dp_2 dp_3 dp_0 であり，太字体の量は三次元ベクトルです．

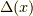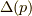ここでフーリエ変換を書いておきます．ここで \Delta(x) と \Delta(p) はフーリエ変換で互いに移り変わります．

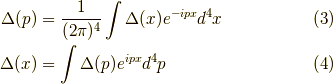
\Delta(p) &= \dfrac{1}{(2 \pi)^4} \int \Delta(x) e^{-ipx} d^4x \tag{3} \\\Delta(x) &= \int \Delta(p) e^{ipx} d^4p \tag{4}

となります．

クラインゴルドン方程式のグリーン関数

クラインゴルドン方程式のグリーン関数が満たす式を書くと，

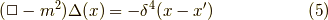
(\Box - m^2)\Delta(x) = -\delta^4(x-x^\prime) \tag{5}

ここでデルタ関数は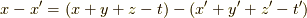， x-x^\prime = (x + y + z - t)-(x^\prime + y^\prime + z^\prime - t^\prime) とすると，

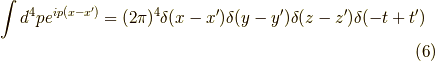
\int d^4p e^{ip(x-x^\prime)}=(2 \pi)^4 \delta(x-x^\prime) \delta(y-y^\prime) \delta(z-z^\prime) \delta(-t+t^\prime) \tag{6}

となります．式(5)に式(4)を代入して，p積分の中身を比較すると，

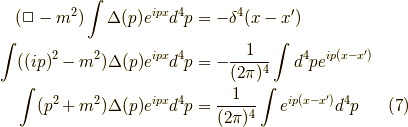
(\Box - m^2)\int \Delta(p) e^{ipx} d^4p &= -\delta^4(x-x^\prime) \\\int ((ip)^2 - m^2)\Delta(p) e^{ipx} d^4p &= -\dfrac{1}{(2 \pi)^4} \int d^4p e^{ip(x-x^\prime)} \\\int (p^2 + m^2)\Delta(p) e^{ipx} d^4p &= \dfrac{1}{(2 \pi)^4} \int e^{ip(x-x^\prime)} d^4p \tag{7}

より，積分の中身を比較して，

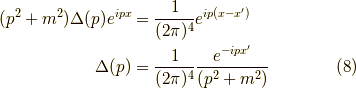
(p^2 + m^2)\Delta(p) e^{ipx} &= \dfrac{1}{(2 \pi)^4} e^{ip(x-x^\prime)} \\\Delta(p) &= \dfrac{1}{(2 \pi)^4} \dfrac{e^{-ipx^\prime}}{(p^2 + m^2)} \tag{8}

となり，なんとか 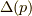\Delta(p) が求まりました．最後に式(4)に求まった 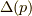\Delta(p) を代入して，

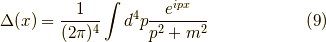
\Delta(x) = \dfrac{1}{(2 \pi)^4} \int d^4p \dfrac{e^{ipx}}{p^2 + m^2} \tag{9}

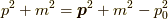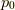ここで， p^2 + m^2 = \bm{p}^2 + m^2 - p_0^2 となり， p_0 での積分に於いて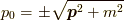， p_0 = \pm \sqrt{\bm{p}^2 + m^2} が特異点となってしまいます．これを避けるために，分母に無限小の因子 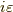i \varepsilon を引きます．ようやく，

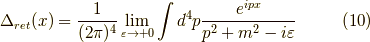
\Delta_{ret}(x) = \dfrac{1}{(2 \pi)^4} \lim_{\varepsilon \to +0} \int d^4p \dfrac{e^{ipx}}{p^2 + m^2 - i \varepsilon} \tag{10}

という形になったわけです．これが遅延グリーン関数 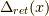\Delta_{ret}(x) です．余談ですが，ここで分母に引くのではなく足すと，先進グリーン関数 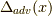\Delta_{adv}(x) となります．

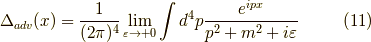
\Delta_{adv}(x) = \dfrac{1}{(2 \pi)^4} \lim_{\varepsilon \to +0} \int d^4p \dfrac{e^{ipx}}{p^2 + m^2 + i \varepsilon} \tag{11}

今日はここまで．お疲れ様でした．