LS多重項((nd)^3)の場合)
量子力学の本を見ると,
LS多重項は, 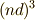 の場合(主量子数
の場合(主量子数 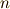 ,方位量子数
,方位量子数 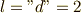 の軌道に3つの電子が入る電子状態),
の軌道に3つの電子が入る電子状態),

とあります.
なぜ, 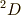 が二つあるの?ということで,すべて多重項を書き出してみることにしました.
が二つあるの?ということで,すべて多重項を書き出してみることにしました.
基本的なこと
今回の話に用いる記法は,参考文献に挙げている小出昭一郎先生の「量子力学(1),(2)」(裳華房)に 従って書いていきます.
原子核の周りを周る電子には,
様々な軌道があります.
主量子数 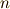 ,方位量子数
,方位量子数 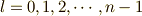 ,
磁気量子数
,
磁気量子数 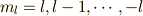 で表せられる軌道がそれです.
ここにさらにスピン
で表せられる軌道がそれです.
ここにさらにスピン  が加わって,
電子の軌道(オービタル)は決定されます.
が加わって,
電子の軌道(オービタル)は決定されます.
このようなオービタルは,スピンの大きさ 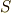 ,軌道角運動量
,軌道角運動量 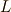 に対して,
(軌道角運動量に対しては,
に対して,
(軌道角運動量に対しては,  とし,以降は,
とし,以降は, 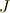 を除いてアルファベット順になって
います.)
を除いてアルファベット順になって
います.) 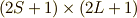 個の「LS多重項
個の「LS多重項 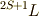 」に分類されます.
例えば
」に分類されます.
例えば  だったら,スピンの大きさ,軌道角運動量がそれぞれ,
だったら,スピンの大きさ,軌道角運動量がそれぞれ, 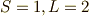 ,
, 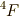 だったら,
だったら,  ,
, 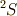 だったら,
だったら, 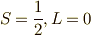 のように表記します.
のように表記します.
電子のようなフェルミ粒子の場合,二つ以上の電子を表す波動関数は,反対称化され, 例えば三粒子の場合,次のようなスレイター行列式で「近似的に」表わされます.(詳しい説明は式の後でします.)
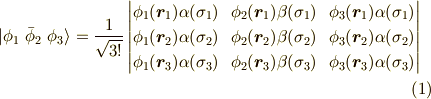
これは,粒子が区別出来ない性質(不可弁別性)より,どれがどの軌道に入っているとは言えないのですが,
粒子1,2,3 ( 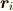 ) が,軌道1,2,3(
) が,軌道1,2,3( 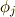 )を占めていると言うことを示しています.
)を占めていると言うことを示しています.
左辺の 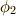 の上のバーは,スピンが下向きということを示しています.
アルファ,ベータというのは,それぞれ,スピンが上向き(
の上のバーは,スピンが下向きということを示しています.
アルファ,ベータというのは,それぞれ,スピンが上向き( 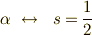 )であること,
スピンが下向き(
)であること,
スピンが下向き( 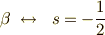 ) であることを示してあります.
シグマというのは,スピンに対する離散的な座標を示してあり,
) であることを示してあります.
シグマというのは,スピンに対する離散的な座標を示してあり, 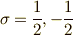 をとり,
をとり,  ,
, 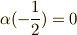 ,
, 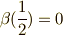 ,
, 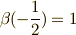 であり,一般的なスピンの状態を
であり,一般的なスピンの状態を 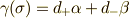 とすると,
とすると, 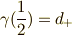 ,
, 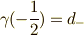 となります.
となります.
フェルミ粒子なので,二粒子の位置 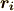 と
と 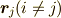 を入れ替えると,
波動関数がマイナス1倍されることが分かります.また,軌道が同じものがあると,
つまり,
を入れ替えると,
波動関数がマイナス1倍されることが分かります.また,軌道が同じものがあると,
つまり, 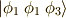 などのような波動関数だと,その波動関数は恒等的にゼロになります.
ここで,今回限りの略記法を取ります.
などのような波動関数だと,その波動関数は恒等的にゼロになります.
ここで,今回限りの略記法を取ります. 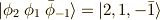 の様に書くことにします.
の様に書くことにします.
角運動量に関する基本的なこと
ここで,角運動量演算子の基本的な性質を書いておきます.
これから複数の粒子に対する角運動量の合成則を考えていきます.
多粒子系を構成する個々の粒子に対する軌道角運動量
を 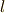 ,その
,その  方向に射影した大きさ(磁気量子数のこと)を
方向に射影した大きさ(磁気量子数のこと)を 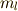 ,スピンの大きさを
,スピンの大きさを  ,その
,その  軸へ射影した大きさを
軸へ射影した大きさを 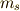 と置きます.
と置きます.
多粒子系(今回は 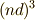 より,3粒子)に対する,角運動量を個々の場合の角運動量を表す文字を大文字に変えたものとします.
つまり,それぞれ
より,3粒子)に対する,角運動量を個々の場合の角運動量を表す文字を大文字に変えたものとします.
つまり,それぞれ 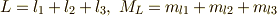 ,
,  とします.
とします.
ここで,  を一般的な角運動量とします.(前者は
を一般的な角運動量とします.(前者は 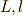 と見ても
と見ても 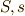 と見ても良く,
後者は,
と見ても良く,
後者は, 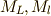 と見ても
と見ても 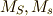 と見ても良い)
角運動量演算子の二乗
と見ても良い)
角運動量演算子の二乗 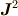 ,角運動量演算子の
,角運動量演算子の  成分
成分 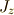 ,
昇降演算子
,
昇降演算子  (ただし
(ただし 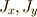 は,角運動量の
は,角運動量の 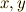 成分,
成分, 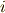 を虚数単位とする)
とし,
を虚数単位とする)
とし,  の量子数で指定される固有状態を
の量子数で指定される固有状態を 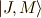 とおくと,
次の関係が成り立ちます. [*] (
とおくと,
次の関係が成り立ちます. [*] ( 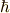 は,プランク定数
は,プランク定数 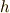 を
を 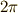 で割ったもの)
で割ったもの)
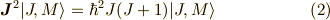
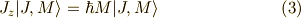
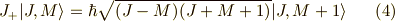
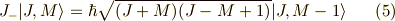
| [*] | これをどうやって求めるかは,例えば,小出昭一郎著,量子力学2(裳華房) p50-p60 などをご覧ください. |
この昇降演算子というものはすぐれもので,一つのLS多重項(一組の 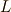 と
と 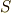 で指定される状態,
で指定される状態, 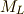 や
や 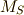 が異なる複数の状態が所属する)で表わされる複数の電子状態の内,
一つでも見つけられれば,昇降演算子で
が異なる複数の状態が所属する)で表わされる複数の電子状態の内,
一つでも見つけられれば,昇降演算子で  成分を変化させることで,残りの状態を求められます.
成分を変化させることで,残りの状態を求められます.
ちなみに,エネルギー的には一つのLS多重項 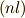 に限れば,
に限れば, 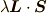 という
エネルギーを持ちます.
という
エネルギーを持ちます. 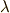 は,詰める電子の数が,
は,詰める電子の数が,  より小さい時には,
より小さい時には, 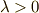 (LとSとは逆向きの方がエネルギー的に安定),
(LとSとは逆向きの方がエネルギー的に安定),  より大きい時には
より大きい時には 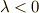 (LとSは同じ方向の方が安定)となります.
(LとSは同じ方向の方が安定)となります.
本題
さて,準備が整ったところで, 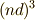 のLS多重項を求めていきましょう.
これは,電子の軌道に電子を詰めていって,閉殼をなす
のLS多重項を求めていきましょう.
これは,電子の軌道に電子を詰めていって,閉殼をなす 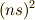 ,
,  の
他に,
の
他に, 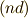 の軌道に電子を3つ詰めた状態のことを
指します.
の軌道に電子を3つ詰めた状態のことを
指します.  は,閉殻をなしているので,
は,閉殻をなしているので, 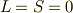 であり,角運動量を持ちません.
よって,一番エネルギーが上の
であり,角運動量を持ちません.
よって,一番エネルギーが上の 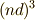 だけを考えれば良いのです.
だけを考えれば良いのです.
冒頭でも書きましたが,今回求めるLS多重項は,以下のようになります.

概要から言うと,個々の粒子の軌道角運動量が  なので,この軌道の波動関数が,
5通りで,(
なので,この軌道の波動関数が,
5通りで,( 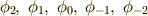 )
スピンの向きが2通り
)
スピンの向きが2通り 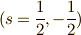 なので,
5×2通りの軌道が存在し,そこに3粒子を詰めるので,
なので,
5×2通りの軌道が存在し,そこに3粒子を詰めるので, 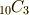 通り,
つまり,120通りの詰め方があります.
はたして,それは正しいでしょうか.
確認してみます.
通り,
つまり,120通りの詰め方があります.
はたして,それは正しいでしょうか.
確認してみます.

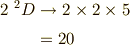
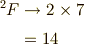

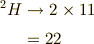
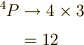
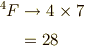
よって,

となり,確かに一致します.
上の状態のうち,まずは 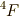 つまり,
つまり, 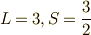 の状態を調べていきます.
の状態を調べていきます.
S=3/2の場合
最初にくるのは,
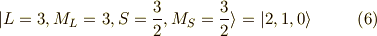
です.この両辺に,下降演算子 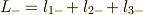 を掛けます.
ここで,例えば
を掛けます.
ここで,例えば 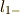 とは,式
とは,式 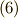 の右辺の一番目の数字
の右辺の一番目の数字 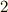 (粒子1の「属する [†] 」軌道の
(粒子1の「属する [†] 」軌道の  )に
かかる下降演算子です.(もっとも,スレイター行列式の性質より,同じ軌道があるとゼロになるので,この場合に生成される
関数
)に
かかる下降演算子です.(もっとも,スレイター行列式の性質より,同じ軌道があるとゼロになるので,この場合に生成される
関数 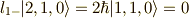 となります.)
一方,
となります.)
一方, 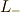 は式
は式 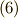 の左辺に掛かります.
の左辺に掛かります.
| [†] | 最初にどの粒子がどの軌道に入るとは言えないといいましたので,正確には,三電子が属する軌道のうちの一番目と考えてください. |
よって,計算すると式 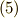 より,式
より,式 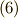 の左辺は,
の左辺は,
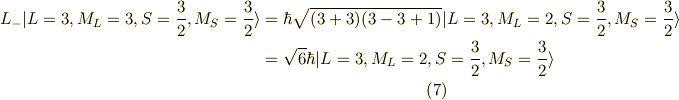
一方,右辺は
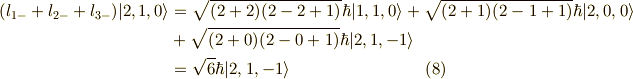
となります.よって,
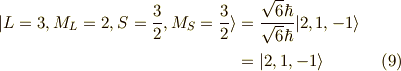
が求まりました.次は, 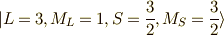 を求めます.
式
を求めます.
式  の両辺に同様に
の両辺に同様に 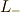 を掛けます.結果は,
を掛けます.結果は,
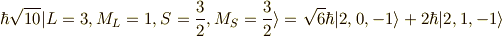
より,
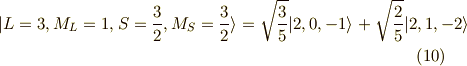
となりました.どうやら正規化された関数が求まるようです.実は更に,直交化もされてあるのです [‡] .
| [‡] | 量子力学の直交定理により,異なる固有値に属する固有ケットは直交化されているのでした.詳しくは, 固有値と固有ベクトル をご覧ください. |
以上の作業を連続して行っていくと,次の関数列が求まります.
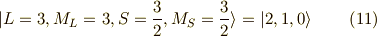
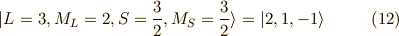
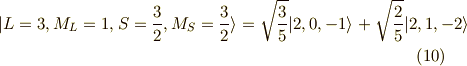
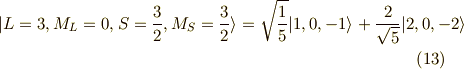
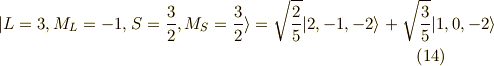
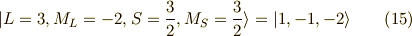
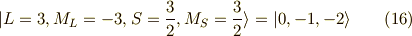
以上が, 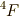 に属する関数です.
に属する関数です.
式 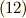 の関数
の関数 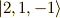 に直交する
に直交する  の関数は取りようがないので,
次に来るのは,
の関数は取りようがないので,
次に来るのは, 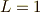 となります.よって,
となります.よって,
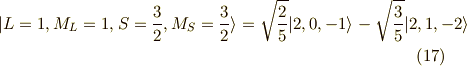

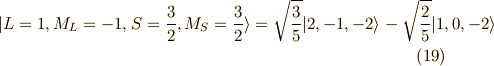
以上が, 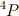 です.
です. 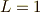 を確認するには,演算子
を確認するには,演算子  を掛けて,
この関数が
を掛けて,
この関数が 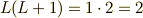 倍されることから,
倍されることから, 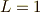 だと結論すればいいのです(式
だと結論すればいいのです(式  参照).
実際に計算してみましょう.すると,
参照).
実際に計算してみましょう.すると,
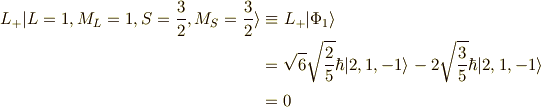
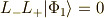
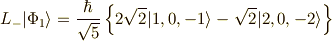
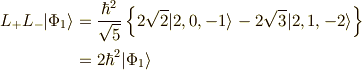

ですから,

よって,確かにこれは 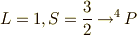 だということが分かりました.
だということが分かりました.
さて,ここまでで, 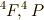 の
の 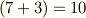 個の波動関数を求めましたが,
さらに,スピンの下降演算子
個の波動関数を求めましたが,
さらに,スピンの下降演算子  をこれらに掛けることによって,
スピン状態が異なる別の状態を作ることができます.実際に式
をこれらに掛けることによって,
スピン状態が異なる別の状態を作ることができます.実際に式 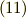 に適用してみましょう.
これも,式
に適用してみましょう.
これも,式 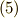 を用いることで計算できます.
を用いることで計算できます.

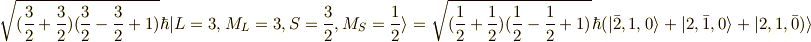
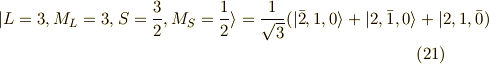
同様に,
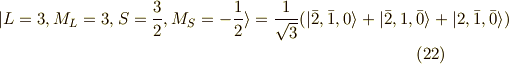
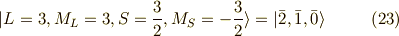
このように以上までで,求めた状態の数は,(軌道の選び方 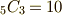 )×(スピンの選び方
)×(スピンの選び方 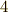 )=40通り
になります.
)=40通り
になります.
L=5 S=1/2
つぎに, 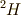 つまり,
つまり, 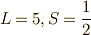 の
の  個の状態を求めます.
この系列で最初にくるのは,
個の状態を求めます.
この系列で最初にくるのは, 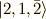 です.
スピンが異なればパウリの排他律が適用されないので,同じ軌道に最大2個まで電子が入ります.
です.
スピンが異なればパウリの排他律が適用されないので,同じ軌道に最大2個まで電子が入ります.
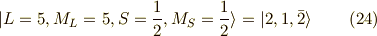
いままで同様に, 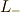 を掛けていきますと,
を掛けていきますと,


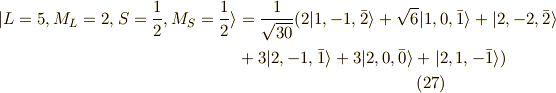
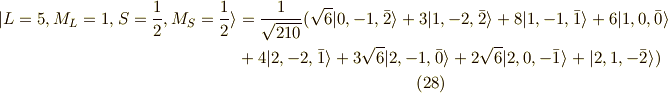
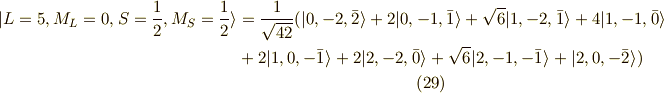

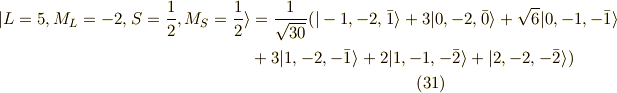
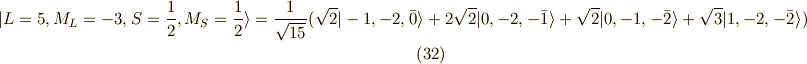
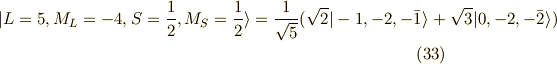
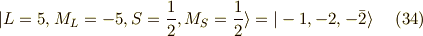
以上の11個の関数に,スピンを反対にした状態を考慮し,2倍して, 計22個の関数ができました.
直交する関数を探せ(L=3,S=1/2)
さて, 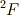 を探すわけですが,今までは直交性を頼りにして,新しい関数系を探してきました.
次からも同じように直交関数を探すことにします.
これから探すのは,
を探すわけですが,今までは直交性を頼りにして,新しい関数系を探してきました.
次からも同じように直交関数を探すことにします.
これから探すのは, 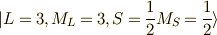 であり,
であり, 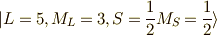 (式
(式 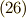 )
と,
)
と, 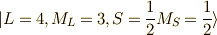 (式
(式 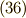 )
に直交する波動関数です.この二関数の直交補空間を求めます.
)
に直交する波動関数です.この二関数の直交補空間を求めます.
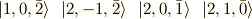
が基底の順番であり,  の係数をこの基底順に
の係数をこの基底順に 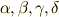 として,
として, 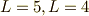 のその係数だけをこの基底順に並べて直交性を調べると,
のその係数だけをこの基底順に並べて直交性を調べると,
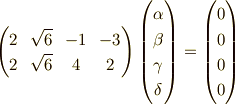
が成り立つはずです.ここで, 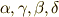 の順番に
入れ替えて,
の順番に
入れ替えて, 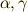 について掃き出し法を行うと,
について掃き出し法を行うと,

よって,
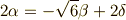
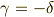
そこで,例えば  としてやると,
としてやると,  となり,
となり,  としてやると,
としてやると,  となります.
となります.
よって,係数を少し調整して, 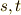 を任意の実数パラメータとして,直交補空間を構成するベクトルを求めると,
を任意の実数パラメータとして,直交補空間を構成するベクトルを求めると,

そして,これに 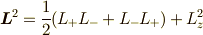 を掛けたときに,
今求めたいのは,
を掛けたときに,
今求めたいのは,  ですから,
ですから, 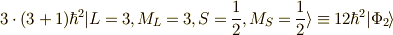 となるようにしてやればいいのです.よって,
となるようにしてやればいいのです.よって,
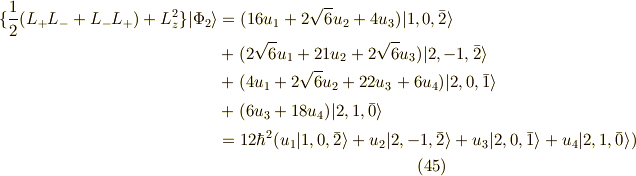
これの解は, 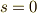 ,
, 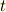 は任意です.
よって,規格化してやると,
は任意です.
よって,規格化してやると,
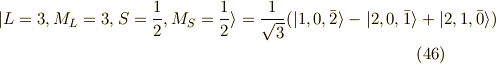
そしてまた, 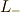 を掛けていきます.
を掛けていきます.
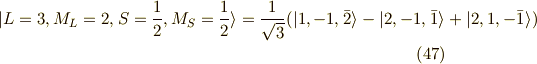
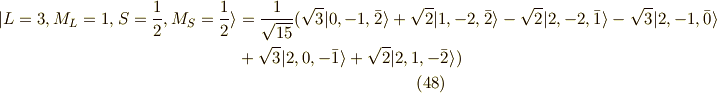

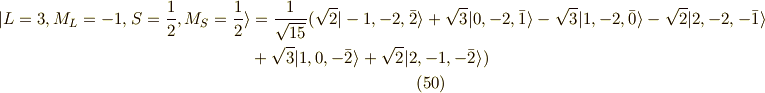
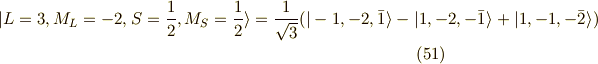
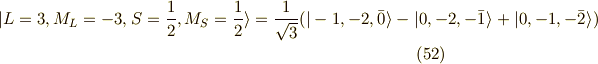
ふぅ,これで 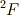 の14個の波動関数(スピンを考慮する)が求まりました.
の14個の波動関数(スピンを考慮する)が求まりました.
直交する関数を探せ(L=2,S=1/2)×2
前の節と同じ様に, 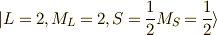 を探します.
を探します. 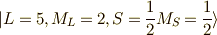 (式
(式 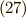 )
と,
)
と, 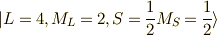 (式
(式 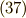 )
と,
)
と,  (式
(式 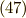 )
に直交する波動関数です.この三関数の直交補空間を求めます.
)
に直交する波動関数です.この三関数の直交補空間を求めます.
基底は,
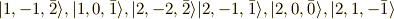
の順番であり,直交する関数の係数だけ抜き出すと,
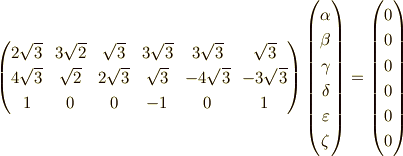
となります.これを掃き出して,例えば,

という形にします.よって,これに直交するベクトル空間 は,
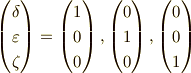
を代入すれば,以下のように求まります.
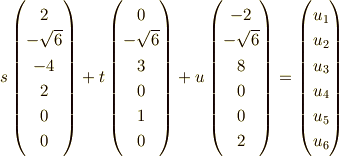
これに 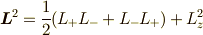 を作用させてみると,
を作用させてみると,
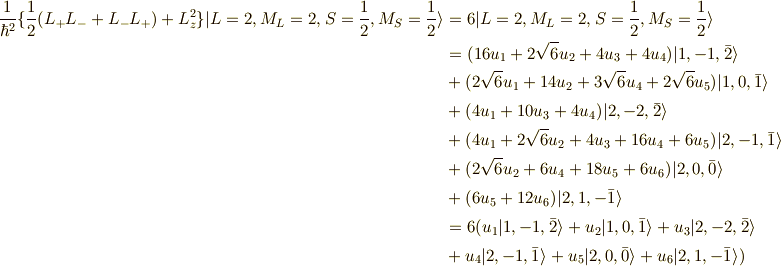
となっています.

より, 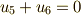 より,
より, 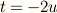 だから,
だから,

今度は,パラメータの自由度が  と
と  で,2になっています.
これが,冒頭で
で,2になっています.
これが,冒頭で 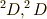 と二つに分けて書いた理由です.
と二つに分けて書いた理由です.
この2自由度の波動関数は固有値が一緒なので,別に直交する必要はないのですが,
一応,全体のバランスを考えて,グラム‐シュミットの直交化法によって,
直交させておくことにします.この二自由度を 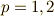 によって区別すると,
によって区別すると,
すると,

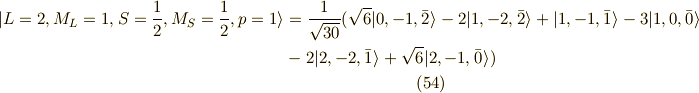
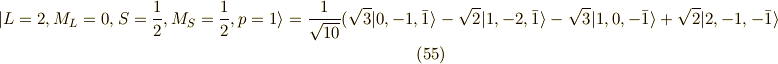
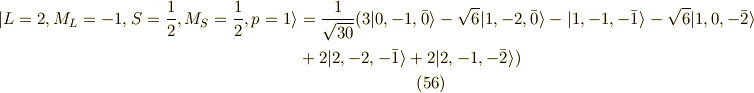
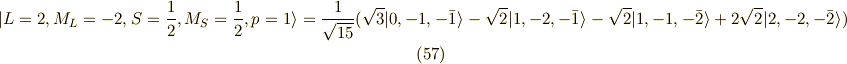
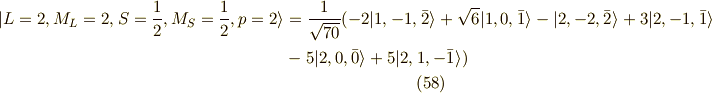
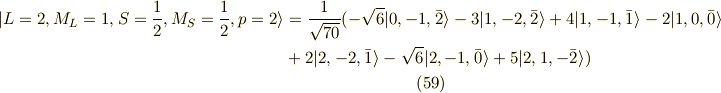
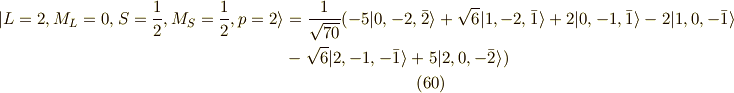
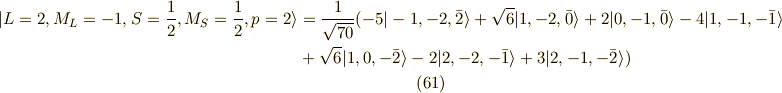

以上が, 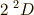 の20個の関数系(スピン含む)です.
の20個の関数系(スピン含む)です.
直交する関数を探せ(L=1,S=1/2)
さあ,いよいよ最後の関数系になりました.  です.
です.
前の節同様に, 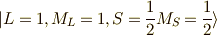 探します.
探します.  (式
(式 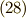 )
と,
)
と,  (式
(式 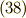 )
と,
)
と, 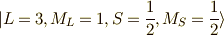 (式
(式 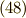 )
と,
)
と, 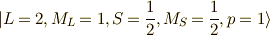 (式
(式  )
と,
)
と, 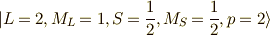 (式
(式 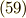 )
に直交する波動関数です.これら五関数の直交補空間を求めます.
)
に直交する波動関数です.これら五関数の直交補空間を求めます.
今度の基底関数は,
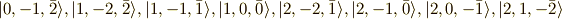
の順番とします.同様に係数だけ書きだすと,
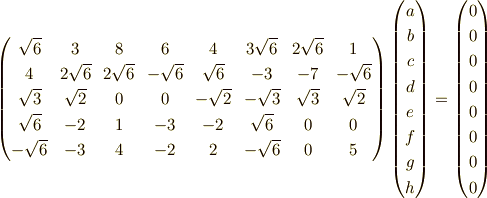
となります.掃き出すと,例えば,
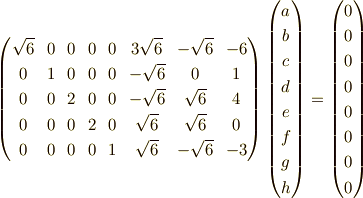
となります.今まで同様に,
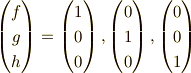
として,直交空間を求めると,
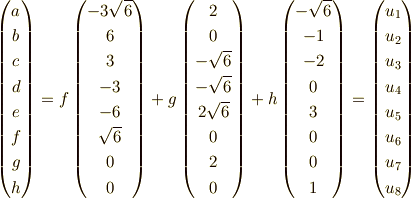
となります.これに, 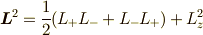 を掛けてやると,
これは,
を掛けてやると,
これは, 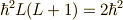 倍されるはずなので,
倍されるはずなので,

ここで, 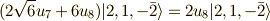 より,
より, 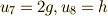 より,
より, 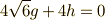 .よって,
.よって,  これを,式
これを,式 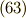 の第一式(
の第一式( 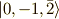 の係数)に注目して,
代入すると,
の係数)に注目して,
代入すると, 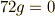 ,つまり,
,つまり,  .よって,
.よって, 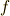 が任意となります.
よって,
が任意となります.
よって,
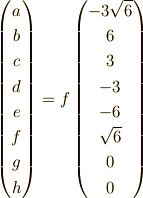
が,この直交補空間を構成し, 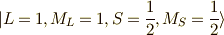 を作ることが分かります.
よって,その状態を具体的に書くと,
を作ることが分かります.
よって,その状態を具体的に書くと,
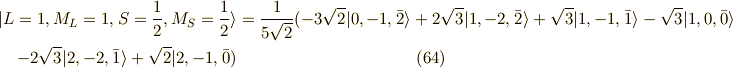
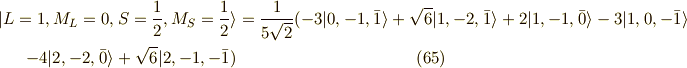
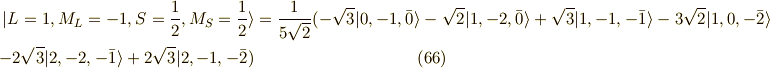
以上で,最後の関数系,  の6個(スピン違いを含む)が求まりました.
これで,すべての
の6個(スピン違いを含む)が求まりました.
これで,すべての 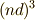 の関数が求まりましたね.
最後にクーロン相互作用で,一番エネルギーが低くなる関数を書いておきます.
それは,
の関数が求まりましたね.
最後にクーロン相互作用で,一番エネルギーが低くなる関数を書いておきます.
それは, 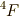 です.これは,フントの規則から結論されると覚えておいてください.
さらに注意しておくと
です.これは,フントの規則から結論されると覚えておいてください.
さらに注意しておくと 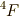 の関数は,更にスピン軌道相互作用により
準位が分裂します.これをJ多重項
といいます.
の関数は,更にスピン軌道相互作用により
準位が分裂します.これをJ多重項
といいます. 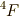 でいうなら式
でいうなら式  〜式
〜式 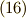 のように分裂するのです.
ただし,スピン
のように分裂するのです.
ただし,スピン 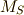 の違うものも忘れないでくださいね.
の違うものも忘れないでくださいね.
今日はここまで.お疲れ様でした^^
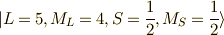 に直交する関数として,
に直交する関数として,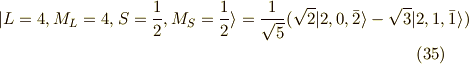
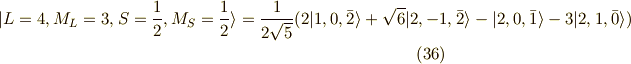
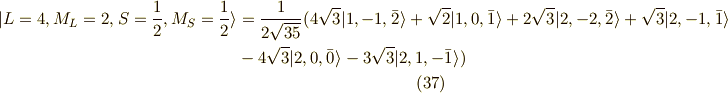

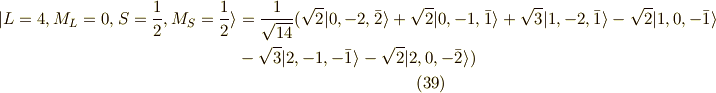
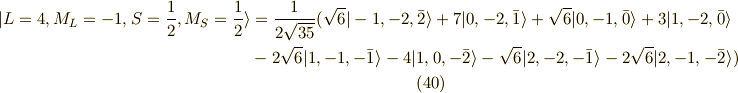
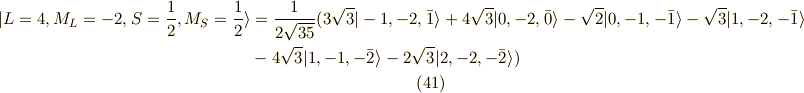
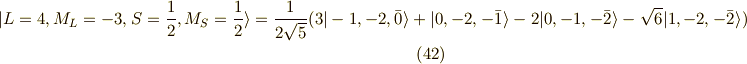
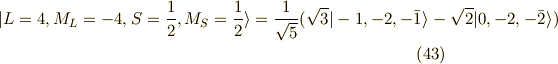
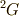 の18個(スピンも考慮)でした.
の18個(スピンも考慮)でした.