任意の方向を向いた3/2スピンの固有状態
この記事では,スピン3/2粒子の固有状態を求めます.
スピン演算子
角運動量演算子 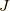 の良く知られた関係
の良く知られた関係
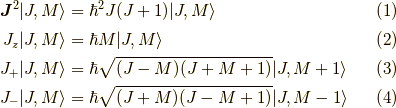
となります.この式の導出には,例えば,下記の小出昭一郎先生の本を参照してください.
これを 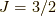 として行列で書くと,
として行列で書くと,
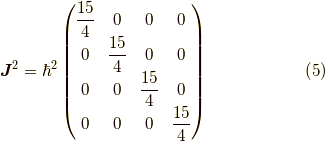
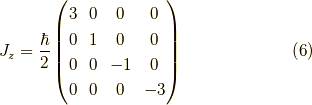
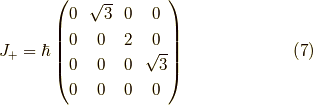
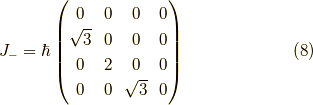
となります.ここで, 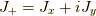 ,
, 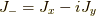 の関係から,
の関係から,
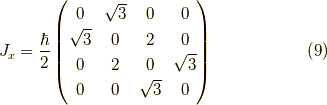
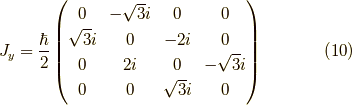
です.任意の方向 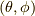 を向いたスピノールは,
を向いたスピノールは,
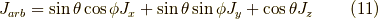
として, 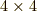 行列の固有値問題
行列の固有値問題

を満たすスピノールの事になります.
この固有値 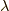 を求めるのに,
を求めるのに, 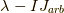 の行列式を求めることは必要ありません.
固有値は任意の方向を向いていても,対称性が同じなので
の行列式を求めることは必要ありません.
固有値は任意の方向を向いていても,対称性が同じなので
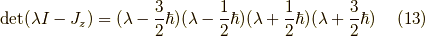
より,
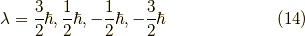
と分かります.
固有値問題を解く
さて, 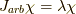 を書いておきましょう.
を書いておきましょう.
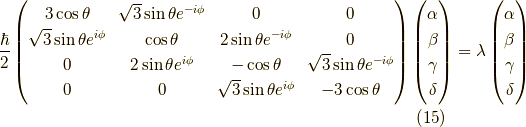
一般に固有値問題は根底にあるのは連立一次方程式なので,解けないことはありませんが,
美しい対称性を持った形を求めるのは,何らかの工夫がいります.
第一成分  の決定でその後の値が決まるのです.
の決定でその後の値が決まるのです.
今回のキーとなるのは,あまり論理的ではないのですが,
3つのスピン 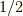 粒子のスピンの合成では,テンソル積が
出てきて,それは
粒子のスピンの合成では,テンソル積が
出てきて,それは 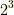 この成分を持つものの第一成分は
この成分を持つものの第一成分は 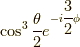 を持っているという知識でした.なお,そのスピン1/2のスピノールは,
を持っているという知識でした.なお,そのスピン1/2のスピノールは,
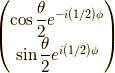
と
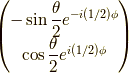
です.(拙記事 任意の方向を向いたスピンのxyz方向固有状態での展開 及び 交換相互作用と任意の方向を向いた二電子スピン 参照)
すると, 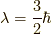 に対して,この第一成分は確かに良い対称性を持っており,
に対して,この第一成分は確かに良い対称性を持っており,
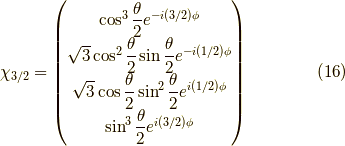
が求まりました.これはスピン 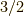 の粒子が
の粒子が 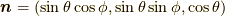 方向に対して,その方向の成分が
方向に対して,その方向の成分が 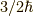 である解を表しています.
である解を表しています.
同様に 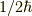 〜
〜 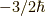 の解は,
の解は,
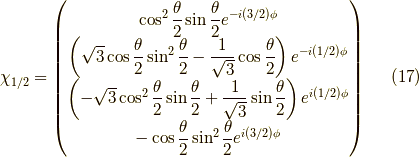
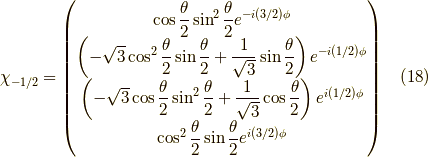
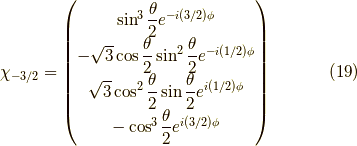
となります.この固有ベクトルと 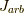 の積を計算してみて,確かに固有ベクトルであることを確認すると良いでしょう.興味深いのは,これらのスピノールは
の積を計算してみて,確かに固有ベクトルであることを確認すると良いでしょう.興味深いのは,これらのスピノールは 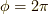 の回転を行っても
の回転を行っても 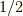 スピノールと同様に符号が反転し,スピンの二価性が容易に見て取れるところです.それでは今日はここまで,お疲れさまでした.
スピノールと同様に符号が反転し,スピンの二価性が容易に見て取れるところです.それでは今日はここまで,お疲れさまでした.