LaTeX表現集

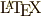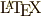この記事では \text{\LaTeX} 数式の表現方法を紹介します． 皆さんが \text{\LaTeX} を使用する際の参考になれば幸いです．

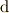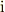なお微分演算子 \mathrm{d} や虚数単位 \mathrm{i} は立体で書いた方が良い，という意見があります． 本記事中では斜体，立体が入り交じっていますがご容赦ください．

基本表現

分数

表示項目 表示 入力
分数 式番号 y=a/x=\frac{a}{x} \tag{88}. y=a/x=\frac{a}{x} \tag{88}.

添字

表示項目 表示 入力
上付添え字 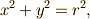x^2+y^2=r^{2}, x^2+y^2=r^2
下付添え字 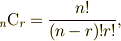_{\it n}\mathrm{C}_{\it r} = \frac{n!}{(n-r)!r!}, _{\it n}\mathrm{C}_{\it r} = \frac{n!}{(n-r)!r!},

微分・積分

表示項目 表示 入力
1次微分 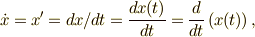\dot x = x^{\prime} = d x/d t=\frac{d x(t)}{d t}=\frac{d}{d t}\left(x(t)\right), \dot x = x^{\prime} = dx/dt=\frac{d x(t)}{d t}=\frac{d}{d t}\left(x(t)\right),
2次微分 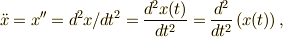\ddot x = x^{\prime \prime} = d^{2} x/d t^{2}=\frac{d^{2} x(t)}{d t^{2}}=\frac{d^{2}}{d t^{2}}\left(x(t)\right), \ddot x = x^{\prime \prime} = d^{2}x/dt^{2}=\frac{d^{2} x(t)}{d t^{2}}=\frac{d}{d t^{2}}\left(x(t)\right),
積分 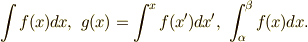\int f(x)dx, \ g(x)=\int^{x} f(x')dx', \ \int_{\alpha}^{\beta} f(x)dx. \int f(x)dx, \ g(x)=\int^{x} f(x')dx', \ \int_{\alpha}^{\beta} f(x)dx.
面積分，線積分 \rm≡\mathrm 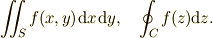\int\mspace{-11mu}\int_{S} f(x,y) \mspace{2mu}{\rm d} x \mspace{2mu}{\rm d}y, \quad \oint_{C} f(z){\rm d}z. \int\mspace{-11mu}\int_{S} f(x,y)\mspace{2mu}{\rm d}x \mspace{2mu}{\rm d}y, \quad \oint_{C} f(z){\rm d}z.
偏微分 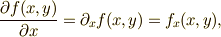\frac{\partial f(x,y)}{\partial x} =\partial_{x}f(x,y)=f_{x}(x,y), \frac{\partial f(x,y)}{\partial x} =\partial_{x}f(x,y)=f_{x}(x,y),

ベクトル・行列・行列式

表示項目 表示 入力
列ベクトルと行列の表示 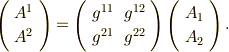\left( \begin{array}{cc} A^{1}\\ A^{2}\\ \end{array} \right) =\left(\begin{array}{cc} g^{11} & g^{12} \\ g^{21} & g^{22} \\ \end{array} \right) \left( \begin{array}{cc} A_{1}\\ A_{2}\\ \end{array} \right). \left( \begin{array}{cc} A^{1}\\ A^{2}\\ \end{array} \right) \left(\begin{array}{cc} g^{11} & g^{12} \\ g^{21} & g^{22} \\ \end{array} \right) \left( \begin{array}{cc} A_{1}\\ A_{2}\\ \end{array} \right).
2点間のベクトル(上の長い矢) 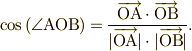\cos\left(\angle \mathrm{AOB}\right) =\frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}} {|\overrightarrow{\mathrm{OA}}|\cdot|\overrightarrow{\mathrm{OB}}|}. \cos\left(\angle \mathrm{AOB}\right)= \frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}} {| \overrightarrow{\mathrm{OA}}| \cdot|\overrightarrow{\mathrm{OB}}|}.
ベクトル内積 dot-product 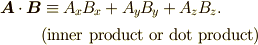{\bm A}\cdot{\bm B} &\equiv A_xB_x +A_yB_y +A_zB_z. \\ &\text{(inner product or dot product)} {\bm A}\cdot{\bm B} \equiv A_xB_x +A_yB_y +A_zB_z.
ベクトル外積 cross-product 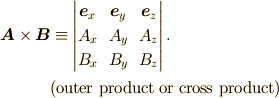{\bm A} \times {\bm B} &\equiv \begin{vmatrix} {\bm e}_{x} & {\bm e}_{y} & {\bm e}_{z} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{vmatrix}. \\ &\text{(outer product or cross product)} {\bm A} \times {\bm B} &\equiv \begin{vmatrix}{\bm e}_{x} & {\bm e}_{y} & {\bm e}_{z} \\ A_x & A_y & A_z \B_x & B_y & B_z \end{vmatrix}.

ベクトル演算子とラプラスの演算子

表示項目 表示 入力
nabla演算子 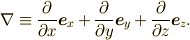\nabla &\equiv \frac{\partial}{\partial x}\bm{e}_{x} +\frac{\partial}{\partial y}\bm{e}_{y} +\frac{\partial }{\partial z}\bm{e}_{z}. \nabla \equiv \frac{\partial}{\partial x}\bm{e}_{x} +\frac{partial}{\partial y}\bm{e}_{y} +\frac{\partial }{\partial z}\bm{e}_{z}.
gradient:勾配 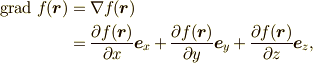\mathrm{grad}\ f({\bm r}) &= \nabla f({\bm r})\\ &=\frac{\partial f({\bm r})}{\partial x}{\bm e}_{x} +\frac{\partial f({\bm r})}{\partial y}{\bm e}_{y} +\frac{\partial f({\bm r})}{\partial z}{\bm e}_{z}, \mathrm{grad}\ f({bm r}) &=\overrightarrow{\bigtriangledown} f({\bm r})\\ &=\frac{\partial f({\bm r})}{\partial x}{\bm e}_{x} +\frac{\partial f({\bm r})}{\partial y}{\bm e}_{y} +\frac{partial f({\bm r})}{\partial z}{\bm e}_{z},
divergence:発散 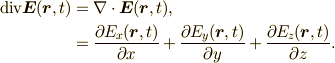\mathrm{div}{\bm E}({\bm r},t) &= \nabla \cdot {\bm E}({\bm r},t),\\ &=\frac{\partial E_{x}({\bm r},t)}{\partial x} +\frac{\partial E_{y}({\bm r},t)}{\partial y} +\frac{\partial E_{z}({\bm r},t)}{\partial z}. \mathrm{div}{\bm E}({\bm r},t)&= nabla \cdot {\bm E}({\bm r},t),\\ &=\frac{\partial E_{x}({\bm r},t)}{\partial x} +\frac{\partial E_{y}({\bm r},t)}{\partial y} +\frac{\partial E_{z}({\bm r},t)}{\partial z}.
rotation:回転 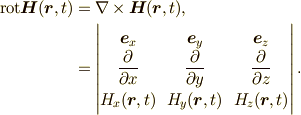\mathrm{rot}{\bm H}({\bm r},t) &= \nabla \times {\bm H}({\bm r},t),\\ &=\begin{vmatrix}{\bm e}_{x} & {\bm e}_{y} & {\bm e}_{z}\\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ H_{x}({\bm r},t) & H_{y}({\bm r},t) & H_{z}({\bm r},t) \end{vmatrix}. \mathrm{rot}{\bm H}({\bm r},t) &= \nabla \times {\bm H}({\bm r},t),\\ &=\begin{vmatrix}{\bm e}_{x} & {\bm e}_{y} & {\bm e}_{z}\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{partial}{\partial z} \ H_{x}({\bm r},t) & H_{y}({\bm r},t) & H_{z}({\bm r},t) \end{vmatrix}.
Laplacian(ラプラシアン：ラプラスの演算子) 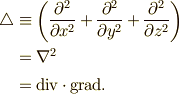\bigtriangleup &\equiv \left( \frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2} +\frac{\partial^2}{\partial z^2}\right)\\ &= \nabla^{2} \\ &= \mathrm{div}\cdot\mathrm{grad}. \bigtriangleup &\equiv \left( \frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2} +\frac{\partial^2}{\partial z^2}\right) \\ &= \nabla^2 \\ &= \mathrm{div}\cdot\mathrm{grad}.
ラプラスの方程式 \text{ } ポアッソンの方程式 \bigtriangleup \Psi({\bm r}) &=0 \qquad \text{solution:}\Psi({\bm r}) \ \text{ harmonic function} \\ &\hookrightarrow \text{Laplace equation} \\ \bigtriangleup \Phi({\bm r}) &=q({\bm r}) \\ &\hookrightarrow \text{Poisson's equation} \bigtriangleup \Psi({bm r}) &=0　& \Psi({bm r}): quad \text{harmonic function} \\ &\hookrightarrow text{Laplace eq.}\\ \bigtriangleup \Phi({bm r}) & = q({bm r}) && hookrightarrow \text{Poisson's equation}

複素数とオイラーの公式

表示項目 表示 入力
複素数 成分により表示 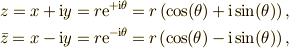z=x+\mathrm{i}y=r\mathrm{e}^{+\mathrm{i}\theta} =r\left(\cos(\theta)+\mathrm{i}\sin(\theta)\right), \\ \bar z=x-\mathrm{i}y=r\mathrm{e}^{-\mathrm{i}\theta} = r\left(\cos(\theta)-\mathrm{i}\sin(\theta)\right), z=x+\mathrm{i}y =r\mathrm{e}^{+\mathrm{i}\theta} =r\left(\cos(\theta)+\mathrm{i}\sin(\theta)\right), \\ \bar z =x-\mathrm{i}y=r\mathrm{e}^{-\mathrm{i}\theta} =r\left(\cos(\theta)-\mathrm{i}\sin(\theta)\right).
オイラーの公式 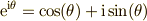\mathrm{e}^{\mathrm{i}\theta} = \cos(\theta) + \mathrm{i}\sin(\theta) \mathrm{e}^{\mathrm{i}\theta} = \cos(\theta) + \mathrm{i}\sin(\theta)
オイラーの逆公式 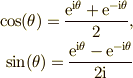\cos(\theta) = \frac{\mathrm{e}^{\mathrm{i}\theta} + \mathrm{e}^{-\mathrm{i}\theta}}{2},\\ \sin(\theta) = \frac{\mathrm{e}^{\mathrm{i}\theta} - \mathrm{e}^{-\mathrm{i}\theta}}{2\mathrm{i}} \cos(\theta) = \frac{\mathrm{e}^{\mathrm{i}\theta} + \mathrm{e}^{-\mathrm{i}\theta}}{2},\\ \sin(\theta) = \frac{\mathrm{e}^{\mathrm{i}\theta} - \mathrm{e}^{-\mathrm{i}\theta}}{2\mathrm{i}}

指数関数と双曲線関数

表示項目 表示 入力
指数関数　←　双曲線関数 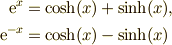\mathrm{e}^{x} & = \cosh(x)+\sinh(x), \\ \mathrm{e}^{-x} & =\cosh(x)-\sinh(x) \mathrm{e}^{x} & = \cosh(x)+\sinh(x), \\ \mathrm{e}^{-x} & =\cosh(x)-\sinh(x)
双曲線関数　←　指数関数 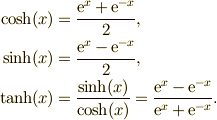\cosh(x) & =\dfrac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2},\\ \sinh(x) & = \dfrac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{2},\\ \tanh(x) & = \dfrac{\sinh(x)}{\cosh(x)} = \dfrac{\mathrm{e}^{x}-\mathrm{e}^{-x}} {\mathrm{e}^{x}+\mathrm{e}^{-x}}. \cosh(x) & =\dfrac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2},\\ \sinh(x) & = \dfrac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{2},\\ \tanh(x) & = \dfrac{\sinh(x)}{\cosh(x)} = \dfrac{\mathrm{e}^{x}-\mathrm{e}^{-x}} {\mathrm{e}^{x}+\mathrm{e}^{-x}}.
式の横並び：簡易法 &&仕切り 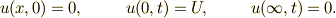u(x,0) =0, && u(0,t) =U, && u(\infty ,t) =0. u(x,0) =0, && u(0,t) =U, && u(\infty ,t) =0.

記号(Symbols)

記号
表示/入力 表示/入力 表示/入力 表示/入力
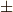\pm \pm \circ \circ \bullet \bullet \cdot \cdot
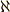\aleph \aleph 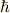\hbar \hbar 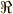\Re \Re 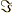\Im \Im
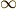\infty \infty 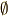\emptyset \emptyset 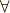\forall \forall 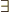\exists \exists
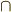\cap \cap 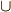\cup \cup 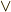\vee \vee 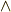\wedge \wedge
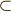\subset \subset 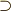\supset \supset \sqsubset \sqsubset \sqsupset \sqsupset
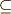\subseteq \subseteq 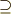\supseteq \supseteq 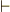\vdash \vdash 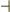\dashv \dashv
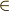\in \in 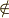\notin \notin 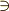\ni \ni 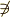\not\ni \not\ni
\parallel \parallel 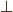\perp \perp 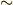\sim \sim 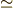\simeq \simeq
\equiv \equiv 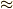\approx \approx 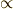\propto \propto 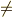\neq \neq
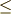\le \le 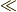\ll \ll 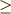\ge \ge 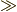\gg \gg

矢印と括弧

矢印と括弧
表示 入力 表示 入力
\gets \gets \longleftarrow \longleftarrow
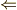\Leftarrow \Leftarrow 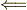\Longleftarrow \Longleftarrow
\to \to \longrightarrow \longrightarrow
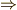\Rightarrow \Rightarrow 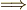\Longrightarrow \Longrightarrow
\leftrightarrow \leftrightarrow \longleftrightarrow \longleftrightarrow
\Leftrightarrow \Leftrightarrow 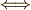\Longleftrightarrow \Longleftrightarrow
\mapsto \mapsto \longmapsto \longmapsto
\hookleftarrow \hookleftarrow \hookrightarrow \hookrightarrow
\rightleftharpoons \rightleftharpoons 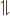\upharpoonleft\hspace{-.24em}\downharpoonright \upharpoonleft\hspace{-.24em}\downharpoonright
\uparrow \uparrow \downarrow \downarrow
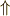\Uparrow \Uparrow 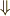\Downarrow \Downarrow
\updownarrow \updownarrow 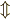\Updownarrow \Updownarrow
\upharpoonleft upharpoonleft \downharpoonright downharpoonright
| | \| \|
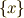\{ x\} \{ x\} 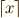\lceil x \rceil \lceil x \rceil
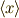\langle x \rangle \langle x \rangle 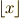\lfloor x \rfloor \lfloor x \rfloor

賢いドットと省略型ドット

賢いdots と 省略型dotsX
用法 表示 入力
賢いdots(カンマ区切り) 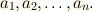a_1,a_2,\dots,a_n. a_1,a_2,\dots,a_n.
賢いdots(二項演算子) 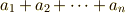a_1 + a_2 + \dots + a_n a_1 + a_2 + \dots + a_n
賢いdots(多項並べ) 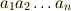a_1 a_2 \dots a_n a_1 a_2 \dots a_n
賢いdots(多重積分) \int \dots \int \int \dots \int
dotsc (commas) 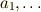a_1,\dotsc a_1,\dotsc
dotsb (binary op. or relations) 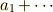a_1 + \dotsb a_1 + \dotsb
dotsm (multiplications) 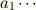a_1 \dotsm a_1 \dotsm
dotsi (integrals) 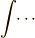\int \dotsi \int \dotsi

ギリシャ文字(小文字，大文字・立体，大文字・斜体)

Greek letters
表示/入力 表示/入力 表示/入力 表示/入力
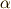\alpha \alpha 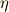\eta \eta \nu \nu \tau \tau
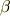\beta \beta 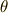\theta \theta 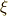\xi \xi \upsilon \upsilon
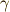\gamma \gamma \iota \iota omicron 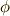\phi \phi
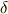\delta \delta 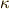\kappa \kappa 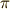\pi \pi 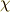\chi \chi
\epsilon \epsilon 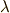\lambda \lambda 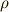\rho \rho 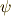\psi \psi
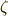\zeta \zeta 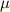\mu \mu 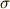\sigma \sigma 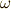\omega \omega
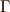\Gamma \Gamma 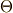\Theta \Theta \Xi \Xi 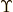\Upsilon \Upsilon
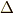\Delta \Delta 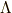\Lambda \Lambda 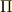\Pi \Pi 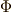\Phi \Phi
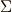    \Sigma \Sigma 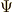\Psi \Psi
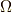      \Omega \Omega
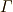\varGamma \varGamma 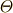\varTheta \varTheta \varXi \varXi 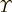\varUpsilon \varUpsilon
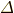\varDelta \varDelta 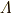\varLambda \varLambda 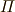\varPi \varPi 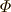\varPhi \varPhi
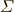    \varSigma \varSigma 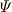\varPsi \varPsi
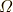      \varOmega \varOmega

数学での「数の種類分け」記号

表示 入力 表示 入力 意味 例
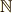\mathbb{N} 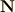\mathbb{N} \mathbf{N} \mathbf{N} 自然数の全体 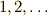1,2,\dots
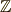\mathbb{Z} \mathbb{Z} 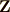\mathbf{Z} \mathbf{Z} 整数全体 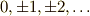0,\pm1,\pm2,\dots
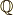\mathbb{Q} \mathbb{Q} 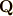\mathbf{Q} \mathbf{Q} 有理数全体 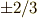\pm 2/3
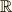\mathbb{R} \mathbb{R} 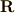\mathbf{R} \mathbf{R} 実数全体 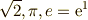\sqrt{2}, \pi, e=\mathrm{e}^{1}
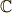\mathbb{C} \mathbb{C} \mathbf{C} \mathbf{C} 複素数全体 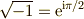\sqrt{-1}=\mathrm{e}^{\mathrm{i}\pi / 2}