力の等価変換
質点の力学ではすべての運動はニュートンの運動の3法則で計算できると説明されていますが, 剛体の力学ではある点の回りのモーメントの計算が必要になります. そのためには,まずモーメントの計算では力が束縛ベクトルである(大きさと向きが同じでも 作用点によって働きが異なる)ことを再認識しなければなりません. ここでは,作用点を明示した束縛ベクトルの表現と計算例を示します.
等価な力とは?
簡単な例として,質量 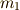 ,
, 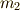 の質点を軽い棒でつないだ下図の剛体を考えます.
の質点を軽い棒でつないだ下図の剛体を考えます.
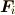 ,
,  はそれぞれ質量
はそれぞれ質量 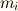 の質点に働く外力,質量
の質点に働く外力,質量 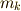 の質点から
質量
の質点から
質量 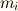 の質点に働く内力です.
の質点に働く内力です.
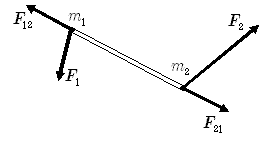
2質点をつないだ剛体
質量 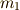 ,
, 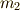 の質点の位置ベクトルをそれぞれ
の質点の位置ベクトルをそれぞれ 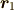 ,
, 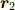 とすると,内力は
とすると,内力は
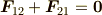
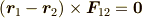
という性質をもっているので,運動方程式
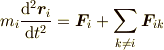
から
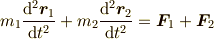
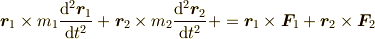
という内力を含まない式が得られ,この微分方程式を解くことによって 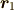 ,
, 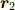 を求めることができます [*] .剛体の運動を考えるときモーメントを計算するのは,
前記の
を求めることができます [*] .剛体の運動を考えるときモーメントを計算するのは,
前記の 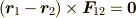 という制約によるものです.
という制約によるものです.
| [*] | 重心 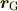 を を
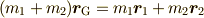 で定義すると,質点の運動方程式と類似の
で定義すると,質点の運動方程式と類似の
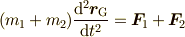 が得られます.
が得られます. |
この剛体に働く力がつり合っているということは 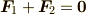 ,
,
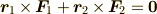 であることを意味します.
このことから,
であることを意味します.
このことから, 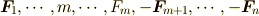 が
つり合っているとき,すなわち
が
つり合っているとき,すなわち
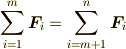
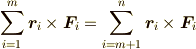
であるとき, 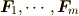 と
と 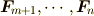 は
等価であると定義します.ここで
は
等価であると定義します.ここで 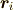 は
は 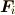 の作用点の位置ベクトルを
表しています.このとき,任意の
の作用点の位置ベクトルを
表しています.このとき,任意の  について
について
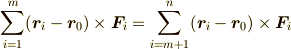
となることを確認してください.
束縛ベクトルの表現
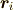 を作用点とする力
を作用点とする力 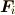 を
を 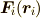 と表しても,
通常は
と表しても,
通常は 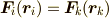 は
は 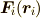 と
と 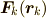 の大きさと向きが等しいと解釈されます.このため,
新しい記号
の大きさと向きが等しいと解釈されます.このため,
新しい記号 ![\bm F_i[\bm r_i]](./0f1d7c4772dead393e3de2a4d5fc47f5.png) を用いて
を用いて
![\sum_{i=1}^m \bm F_i[\bm r_i] = \sum_{i=m+1}^n \bm F_i[\bm r_i]](./a24499d2db30d31342e1fec6e6f3f5a0.png)
の意味を
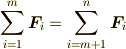
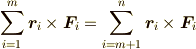
で定義します.この定義からただちに 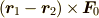 ならば
ならば
![\bm F_0[\bm r_1] = \bm F_0[\bm r_2]](./187f6ab4610dc3fbac4fc13b38d046ef.png) (力はその作用線上を移動しても働きは変わらない)
という性質が導かれます [†] .
(力はその作用線上を移動しても働きは変わらない)
という性質が導かれます [†] .
| [†] | 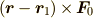 となる点 となる点  の集合を力 の集合を力
![\bm F_0[\bm r_1]](./edc654b6055df63de902ee08ad37d49e.png) の作用線といいます. の作用線といいます. |
二つの力の合力
与えられた ![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
, ![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) に対して
に対して
![\bm F_1[\bm r_1] + \bm F_2[\bm r_2] = \bm F_3[\bm r_3]](./df2805b5cd5b359797ec0e61fa470fb8.png)
となる ![\bm F_3[\bm r_3]](./d3c19aa41b33fa29c6e237d0ec051d3b.png) が存在するとき,
が存在するとき, ![\bm F_3[\bm r_3]](./d3c19aa41b33fa29c6e237d0ec051d3b.png) を
を ![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
,
![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) の合力といいます.
の合力といいます. ![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
, ![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) が
同一平面上にあれば,
が
同一平面上にあれば, 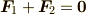 ,
, 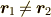 の場合を除いて,合力が存在します.
の場合を除いて,合力が存在します.
偶力
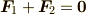 ,
, 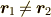 のとき,
のとき, ![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
,
![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) の合力は存在しません.このような力の組
の合力は存在しません.このような力の組 ![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
,
![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) を偶力といい,以下では
を偶力といい,以下では ![\bm F_0[\bm r_1] - \bm F_0[\bm r_2]](./dfeddb7821cd80b76d34b9758bbddb54.png) を
を ![\bm F_0[\bm r_1, \bm r_2]](./017261c10d9283c24bbddaf7445e4250.png) と略記します.
と略記します.
偶力のモーメントが自由ベクトルであること,すなわち任意の  について
について
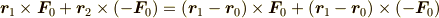
が成立することや,偶力 ![\bm F_0[\bm r_1, \bm r_2]](./017261c10d9283c24bbddaf7445e4250.png) と
偶力
と
偶力 ![c^{-1} \bm F_0[c(\bm r_1 - \bm r_2), \bm 0]](./4c7453d840dfcc00b56718aa4b0b28f2.png) のモーメントが等しいこと等が
容易に確かめられます.
のモーメントが等しいこと等が
容易に確かめられます.
3次元の力の等価変換
![\bm F_1[\bm r_1]](./ca1e0a53d9d3f16e925a4d838bb2a620.png) ,
, ![\bm F_2[\bm r_2]](./82e51ff279b94b29e8108c37d2cf81c8.png) が同一平面上になければ
これらの合力は存在しませんが,任意の
が同一平面上になければ
これらの合力は存在しませんが,任意の  について
について
![\bm F_1[\bm r_1] + \bm F_2[\bm r_2]= \bm F_3[\bm r_0] + \bm F_4[\bm r_4, \bm r_0]](./3dae3fb2e42ec9fd8a89255161baac89.png)
が成立するように 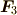 ,
, 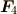 ,
, 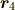 を選ぶことができます.
を選ぶことができます.
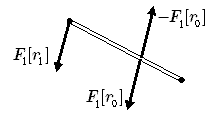
![\bm F_i[\bm r_i]](./0f1d7c4772dead393e3de2a4d5fc47f5.png) の等価変換
の等価変換
例えば, ![\bm F_i[\bm r_i]](./0f1d7c4772dead393e3de2a4d5fc47f5.png) を
を
![\bm F_i[\bm r_i] = \bm F_i[\bm r_0] + \bm F_i[\bm r_i] - \bm F_i[\bm r_0]= \bm F_i[\bm r_0] + \bm F_i[\bm r_i, \bm r_0]](./4da6fad2e626e4f4c634aee626025984.png)
と変形して加算した式
![\sum_{i=1}^2 \bm F_i[\bm r_i]= \left( \sum_{i=1}^2 \bm F_i \right)[\bm r_0] + \sum_{i=1}^2 \bm F_i[\bm r_i, \bm r_0]](./146512f8733fd113b05b92e748c3797e.png)
の右辺第2項は偶力の和ですから,自由ベクトルであるこれらのモーメントの和

は容易に計算でき, 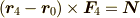 を満足する
を満足する 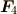 ,
,
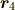 が求められます [§] .
が求められます [§] .
| [§] | 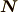 が が 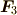 と平行でないとき, と平行でないとき, 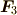 と平行な偶力の成分を と平行な偶力の成分を
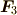 に加算し(合力が存在します),これと に加算し(合力が存在します),これと 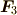 と直交する偶力
(モーメントは と直交する偶力
(モーメントは 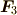 と平行)との和に変形できます. と平行)との和に変形できます. |
上式で  が任意の点でよかったことを思い出すと,多数の3次元ベクトル
が任意の点でよかったことを思い出すと,多数の3次元ベクトル
![\bm F_1[\bm r_1], \cdots , \bm F_n[\bm r_n]](./1806faa5c03dd0f8ef80d39aa91901f2.png) についても
についても
![\sum_{i=1}^n \bm F_i[\bm r_i]= \bm F_{n+1}[\bm r_0] + \bm F_{n+2}[\bm r_{n+2}, \bm r_0]](./f2c9211a3a9ad360e9cbfa41b6db890d.png)
となる 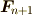 ,
, 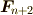 ,
,  が存在することが分かります.
が存在することが分かります.
一様な密度の剛体に働く力
重力
![\bm F_0[\bm r_0 - \bm r_1] + \bm F_0[\bm r_0 + \bm r_2] = 2 \bm F_0[\bm r_0]](./aa8e50a5aa7959e183c0ed7773596898.png) ですから,密度が一様で,点
ですから,密度が一様で,点  に関して対称な剛体に働く重力は,重心を
作用点とし,大きさと向きが力の総和に等しい力と等価であることが分かります.
に関して対称な剛体に働く重力は,重心を
作用点とし,大きさと向きが力の総和に等しい力と等価であることが分かります.
例えば,両端が 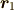 ,
, 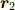 にある質量
にある質量 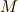 の棒に働く重力は,棒を
の棒に働く重力は,棒を 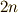 個の微小領域に等分して点対称な位置にある微小領域の対を考えると,各対の合力の
作用点はすべて棒の中心になり,これらの合力の総和が棒に働く重力と等しくなります.
個の微小領域に等分して点対称な位置にある微小領域の対を考えると,各対の合力の
作用点はすべて棒の中心になり,これらの合力の総和が棒に働く重力と等しくなります.
固定点から受ける力
剛体が固定点の回りを運動しているとき,通常は固定点回りの角運動量の時間微分が
固定点回りの外力のモーメントの総和に等しいとして運動方程式を解きます.この場合,
固定点に働いている力を計算する必要はありませんが,上記の説明と関連付けるために
固定点  に働く力が
に働く力が ![\bm F_0[\bm r_0]](./bfd60874b22c6e34936bdaca646a4ab9.png) , その他の外力(重力は重心に集中
しているとして扱います)が
, その他の外力(重力は重心に集中
しているとして扱います)が ![\bm F_i[\bm r_i]](./0f1d7c4772dead393e3de2a4d5fc47f5.png)
 である場合
について考えましょう.
である場合
について考えましょう.
この剛体に働く力は
![\bm F[\bm r] = \left( \sum_{i=0}^n \bm F_i \right) [\bm r]+ \sum_{i=0}^n \bm F_i[\bm r_i, \bm r]](./2f8f3bfb6eb4fc08872a24fc60807d6c.png)
と等価ですから, 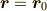 とおくと
とおくと  回りの角運動量を求める
方程式から
回りの角運動量を求める
方程式から 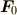 が消えてしまいます.つまり,
が消えてしまいます.つまり, 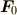 を求める必要がなければ
運動量を求める方程式は考えなくてよいのです.
を求める必要がなければ
運動量を求める方程式は考えなくてよいのです.
数値例について
「二つの力の合力」では,数値例に ![\bm F_1[\bm r_1] = (0, -F)[(0, 0)]](./848c1d80d74cb194b058fdeac93bbab7.png) ,
,
![\bm F_2[\bm r_2] = (0, -2F)[(3r, 0)]](./c14884907c5a4334b56fd962e8efba15.png) のような表現を用いました.この点について
補足します.
のような表現を用いました.この点について
補足します.
通常,物理量を表す文字は単位を含んでいます.例えば,速さ  で時間
で時間 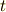 だけ
移動したときの移動距離は
だけ
移動したときの移動距離は 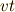 であるといったとき,
であるといったとき,  や
や 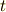 の単位は自由に選べます.
の単位は自由に選べます.
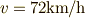 ,
,  ならば
ならば 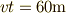 です.
なお,速さ
です.
なお,速さ  で
で 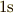 間移動したときの移動距離は
間移動したときの移動距離は  ではなく
ではなく
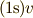 です [¶] .上記の
です [¶] .上記の ![(0, -2F)[(3r, 0)]](./01505e6cce116da401216523a7ceab92.png) のような数値例は
のような数値例は
![(0, -2 \mathrm{N})[(3 \mathrm{m}, 0)]](./082e85851148c77d13b2cc98ccfe1fed.png) のような表現より分かりやすいと思います.
のような表現より分かりやすいと思います.
| [¶] | 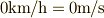 だから だから 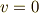 の右辺に単位は不要ですが,
温度 の右辺に単位は不要ですが,
温度 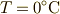 の単位は省略できません.
(蛇足ですが,熱容量や比熱に使われる温度差の の単位は省略できません.
(蛇足ですが,熱容量や比熱に使われる温度差の 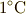 は は
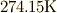 でなく でなく 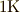 です. です. ![[\mathrm J]](./8bec412b4cb234c48aa59a684c077c5f.png) でない でない
![[\mathrm N \cdot \mathrm m]](./d9f7da24f93bab544fc227e6b91d1099.png) , 無次元でない , 無次元でない ![[\mathrm m / \mathrm m]](./7b3f42b3d053e5beaec4106403ca9f27.png) 等,
単位については苦し紛れの区別がいくつかあります.) 等,
単位については苦し紛れの区別がいくつかあります.) |
あとがき
ここで述べた内容はすべて私が学生のときに学んだ教科書[1](古書,ISBNなし)に書かれて います.既知の事柄を珍奇な記号を使って書き換えただけだと感じた方が多いと思いますが, モデリング,記法,プログラミング等に関心のある高校生・大学生諸君のために所属学会の 研究会で発表した内容を補足し,数値例も付け加えて紹介しました.教科書・参考書を超えて 自分でいろいろ工夫してほしいというのが筆者の願いです.
参考文献
- 著,『 力学?』( 丸善, 1958, 80-86)
 となる
となる  ,
,  が
存在し,
が
存在し,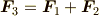

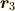 は2力の作用線の交点).
は2力の作用線の交点).![\bm F_1[\bm r_1] = (F, 0)[(2r, 0)]](./42ca67c3f3cdf806c2ea24365d3d13fa.png) ,
, ![\bm F_2[\bm r_2] = (0, F)[(0, 2r)]](./febc5a6876e8bd675bf4cc299542833b.png) のとき,
のとき,
![\bm F_3[\bm r_3] = (F, F)[(0, 0)]](./681450d7c6f0d96420d43c0030e411a3.png) となります.ただし,
となります.ただし, 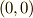 は
剛体上にないので,
は
剛体上にないので, 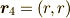 を求め,
を求め, ![\bm F_3[\bm r_4] = (F, F)[(r, r)]](./fc9ad6faa0a787d54fdea7e84e3868a9.png) を
合力とする方が自然でしょう
を
合力とする方が自然でしょう 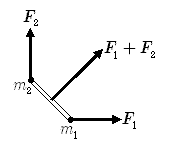
![(F, 0)[(2r, 0)] + (0, F)[(0, 2r)]](./c7d3ddf1f788e19155887fbd0a573eb1.png)
 ,
, 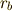 ,
, 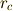 について
について
![(F, F)[(0, 0)] = (F, 0)[(r_a, r_b)] + (0, F)[(r_c, r_a)]](./2540fc9e44412d4625b3d9b1ec6dca42.png) が成立します.
が成立します.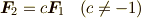 であれば,
であれば,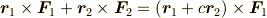
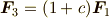
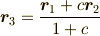

![\bm F_3[\bm r_3] = (0, -3F)[(2r, 0)]](./ede74b22b94e113874b5dc647785e938.png) となります.
となります.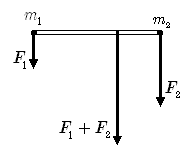
![(0, -F)[(0, 0)] + (0, -2F)[(3r, 0)]](./4e4ac6c3935e6df31fded899c54aace5.png)