斜面をすべる運動
運動方程式という基本法則を使って,なめらかな斜面をすべる物体の運動を数式という言語で記述してみます.「なめらかな」という言葉は物理でよく出てきますが,これは摩擦だとかの運動を複雑にする要素を考えなくてもいい,という意味です.
これからやることでは,微分積分の考え方を使います.高校で習う物理では運動方程式をいきなり積分したりしないので,ちょっととっつきにくいですが,最終的にはこの方法のほうが覚えることも少ないですし豊かな内容を含んでいます.そのうち慣れるので,めんどくさそうですが数式にも注意を払って読んでみてください.
斜面と物体
下の図のような状況を考えます.角度 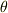 で傾いたなめらかな斜面に質量
で傾いたなめらかな斜面に質量 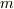 のなにかがあります.
のなにかがあります.
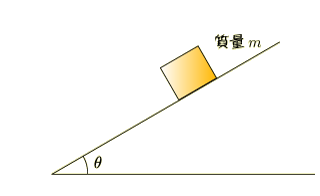
で,まずは想像してみます.この物体はこのあとどうなりますか.斜面はなめらか(ツルツル)なので,当然すべり落ちます.これから考えることは,この物体がどんなふうにすべるかです.この状態から 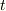 秒後にはどんな速度でどれくらいの距離だけすべったか分かればいいでしょう.
秒後にはどんな速度でどれくらいの距離だけすべったか分かればいいでしょう.
働く力をみつける
この物体に働く力を考えます.なによりもさきに思い浮かべないといけないのは「重力」です.地球上にある物体は質量に応じて重力という力を受けますので.質量が 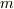 なので,重力加速度を
なので,重力加速度を 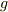 とするとその大きさは
とするとその大きさは 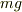 です.そして物体に触れているものからも力を受けます.この場合は斜面ですね.この力は垂直抗力と呼ばれます.大きさはまだよく分からないので,
です.そして物体に触れているものからも力を受けます.この場合は斜面ですね.この力は垂直抗力と呼ばれます.大きさはまだよく分からないので,  としておきます.
としておきます.
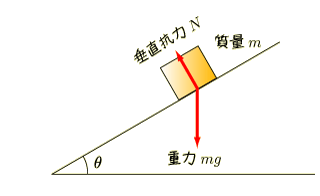
実際には空気にも触れているでしょうが,いまは考えないことにします.だから働く力はこれだけです.
座標軸を設定する
つぎにすることは,座標軸の設定です.座標は基本的に自由に決めていいです.ただしいいかげんに決めるとあとで大変なだけなので,なるべく簡単になるように決めておきます.いまは斜面に沿ってしか動きようがないので,斜面に沿って下向きを正方向として  軸を設定します.
軸を設定します.
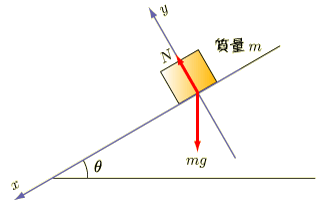
そしてそれに垂直に 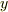 軸を設定します.
軸を設定します.
力を座標軸に沿った成分に分解する
座標軸を決めたので,働く力を軸に沿った成分に分解します.それには 三角比 を使います.垂直抗力は軸に沿っているので分解しなくていいですね.分解するのは重力です.
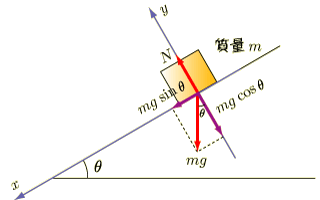
図で  軸と
軸と 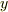 軸の交点に
軸の交点に 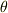 とつけていますが,これは平面の幾何学からそうなります.錯角とか対頂角とかそういうやつ.名前はよく覚えてません.それでまあ,図のように分解できます.
とつけていますが,これは平面の幾何学からそうなります.錯角とか対頂角とかそういうやつ.名前はよく覚えてません.それでまあ,図のように分解できます.
y 軸方向には動かない
以上で準備が整いました.あとは数式にしていきます.まずは簡単そうな 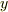 軸ですが,
軸ですが,
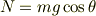
という等式が成り立つのはいいでしょうか.これは垂直抗力の性質そのままです.経験的に考えて,いまのような状況では物体が 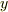 軸方向に動き出すことはありませんよね.動く理由がありません.だから垂直抗力
軸方向に動き出すことはありませんよね.動く理由がありません.だから垂直抗力 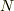 と重力の
と重力の 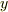 成分
成分 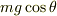 はつり合っていると考えます.これ以上考えることもないので,
はつり合っていると考えます.これ以上考えることもないので, 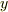 軸についてはこれでおしまいです.
軸についてはこれでおしまいです.
x 軸方向には運動方程式
最初にイメージしたように,  軸方向(斜面に沿った方向)にはすべり落ちるのでした.動かす力は重力の
軸方向(斜面に沿った方向)にはすべり落ちるのでした.動かす力は重力の  成分,
成分, 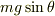 であります.働く力が分かっているので,運動方程式
であります.働く力が分かっているので,運動方程式 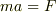 を立てることができます.力
を立てることができます.力 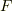 は
は 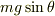 なので,この状況の運動方程式は
なので,この状況の運動方程式は
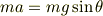
と書けます.ここで加速度  を微分形で表します.
を微分形で表します.  は位置
は位置  の 2階微分
の 2階微分 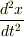 ですから
ですから
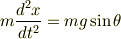
となり,微分方程式のできあがりです.これがすべてを表現しています.あとは運動方程式を解いて 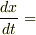 とか
とか 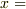 とかの形に変形すれば,速度(
とかの形に変形すれば,速度( 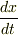 は速度のこと)や位置が分かります.ここからは物理というより数学の問題ですね.しばらく数式をひねくりまわしますが,おつきあいください.
は速度のこと)や位置が分かります.ここからは物理というより数学の問題ですね.しばらく数式をひねくりまわしますが,おつきあいください.
運動方程式を解く
物理的なお膳立てが済んだので,機械的に解いていきます.これは変数分離形の微分方程式( 変数分離形 のページも参考にしてください)です.
速度の計算
運動方程式の両辺を 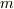 で割ると
で割ると
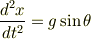
ここで左辺の2階微分はつぎのように書けます.
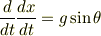
両辺を時間  で積分すれば
で積分すれば 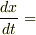 の形になるのですが,この積分は簡単です.
の形になるのですが,この積分は簡単です. 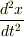 は
は 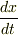 を
を 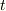 で微分したものですから,
で微分したものですから, 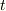 で積分したら
で積分したら 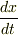 になるだけです.積分の形でかくと
になるだけです.積分の形でかくと
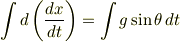
となります.積分の計算ですが,右辺は定数なので単に 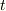 を掛けます.そして不定積分なので積分定数
を掛けます.そして不定積分なので積分定数 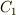 を付けておきます.
を付けておきます.
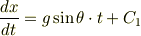
これは 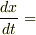 になっているので,速度が分かったことになります.左辺は速度の記号
になっているので,速度が分かったことになります.左辺は速度の記号  で書いたほうが分かりやすいですかね.速度の式は,つぎのようになります.
で書いたほうが分かりやすいですかね.速度の式は,つぎのようになります.

位置の計算
位置  についても知りたいので,式(1)の両辺をもう1回積分します.すこし変形して
についても知りたいので,式(1)の両辺をもう1回積分します.すこし変形して
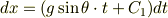
積分の式で書くと
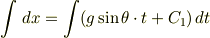
であり,積分計算をすると位置の式がつぎのように表せます.
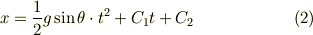
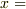 になったので位置についても分かりました.これでおしまいなんですが,もう少し物理的意味を考えておきましょう.いま生まれた積分定数についてです.
になったので位置についても分かりました.これでおしまいなんですが,もう少し物理的意味を考えておきましょう.いま生まれた積分定数についてです.
積分定数の意味
積分定数は単なる定数ではなく,物理的な意味をもっています.
速度の式の積分定数
1つめの積分定数 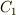 は,
は, 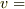 の式の右辺にあります.速度の式
の式の右辺にあります.速度の式
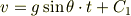
によると, 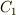 の単位は速度の単位と等しい,ということが分かりますから
の単位は速度の単位と等しい,ということが分かりますから 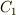 の単位は速度の単位 m/s(メートル毎秒)になるハズです.なので
の単位は速度の単位 m/s(メートル毎秒)になるハズです.なので 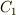 はなんらかの速度です.試しに速度の式に
はなんらかの速度です.試しに速度の式に 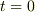 を入れてみましょう.すると
を入れてみましょう.すると
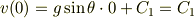
となり,ずいぶん簡単になりました. 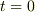 のとき
のとき 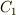 は
は 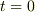 のときの速度
のときの速度 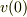 に等しい,となってます.これを「初速度」といい,ふつう
に等しい,となってます.これを「初速度」といい,ふつう 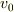 という記号で書きます.積分定数を初速度とした速度の式は,つぎのようになります.
という記号で書きます.積分定数を初速度とした速度の式は,つぎのようになります.
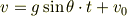
位置の式の積分定数
2つめの積分定数 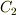 は,
は, 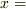 の式の右辺にあり,距離と等しくなっています.位置の式
の式の右辺にあり,距離と等しくなっています.位置の式
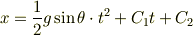
によると, 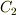 の単位は距離の単位 m(メートル)になるハズです.ですから,さきほどと同様式(2)に t = 0 を入れると簡単になることが期待できます.
の単位は距離の単位 m(メートル)になるハズです.ですから,さきほどと同様式(2)に t = 0 を入れると簡単になることが期待できます. 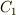 は
は 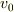 と書いておきます.代入すると
と書いておきます.代入すると
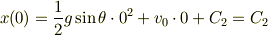
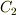 は
は 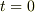 のときの位置
のときの位置 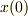 に等しいとなってます.これは…なんていうんだろ,「初期位置」とでもいうんでしょうか.ふつう
に等しいとなってます.これは…なんていうんだろ,「初期位置」とでもいうんでしょうか.ふつう 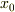 という記号で書きます.以上より,積分定数を書き換えた位置の式は
という記号で書きます.以上より,積分定数を書き換えた位置の式は
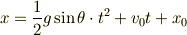
となります.これらは高校物理で習う「等加速度運動の速度の公式」と「等加速度運動の距離の公式」そのものです.だからもうあんな変なもの暗記しなくてもいいんですね.その代わりに微分方程式の解き方をマスターしなくちゃならいんですが.微分方程式が解ければもっと複雑な,抵抗力がある場合だとかその他もろもろの状況を同じやり方で解くことができます.ちなみに僕は簡単なやつしか解けないので,これから覚えようと思います.