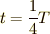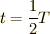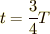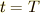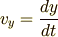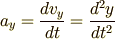単振動 〜等速円運動の射影〜
単振動 [*] は,物理学のいろいろな場面で登場する重要な運動です.ばねの運動で登場したり, 振り子の運動で登場したり,はたまた電気振動なんていうものもあります. 以下では,等速円運動の射影として単振動を紹介し,速度や加速度についてもみていきます. 等速円運動 についてまだ学習していない人は,そちらからご覧下さい.
| [*] | 「単振動」という表現の他に,「調和振動」という表現もよく使います.「単振動」と「(1次元)調和振動」は同じものを指します.また,「調和振動子」と言った場合には,振動しているもの(振動の性質をもつもの)を指します. |
単振動は等速円運動の射影だ
半径 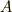 の円周上を運動する 等速円運動 を考えます.分かりやすいように,
の円周上を運動する 等速円運動 を考えます.分かりやすいように,  平面状に原点を中心とする
半径
平面状に原点を中心とする
半径 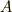 の円を描いておきます.物体は時刻
の円を描いておきます.物体は時刻 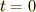 のとき点
のとき点 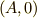 を出発して,角速度
を出発して,角速度 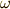 で運動します.
で運動します.

この等速円運動について,  軸への射影を考えてみましょう.時間を追って図を描くと,以下のようになります(
軸への射影を考えてみましょう.時間を追って図を描くと,以下のようになります(  は周期).
は周期).
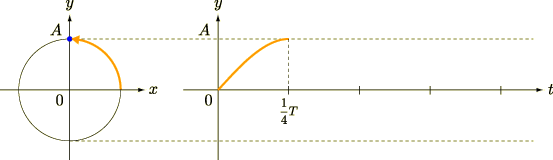
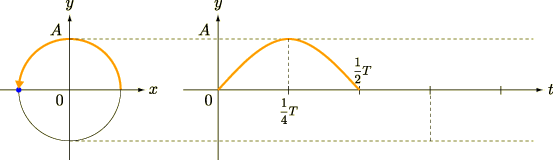
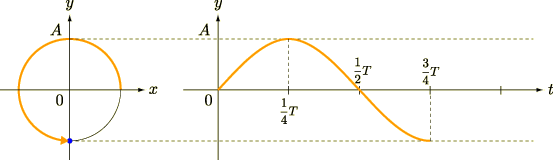
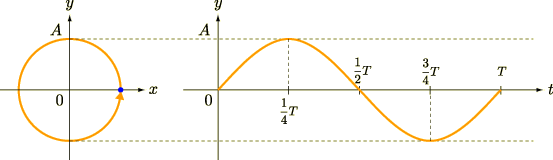
この 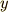 軸への射影こそが,単振動だというわけです.
軸への射影こそが,単振動だというわけです.
変位はどのように表されるか
変位 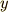 がどのように表されるか,考えてみましょう.時刻
がどのように表されるか,考えてみましょう.時刻 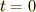 のとき
点
のとき
点 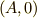 を出発して,角速度
を出発して,角速度 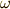 で運動した場合,
で運動した場合, ![t[{\rm s}]](./3561d94b4ac71d35620d338eab3c9e6f.png) 後には以下のようになっているはずです.
後には以下のようになっているはずです.
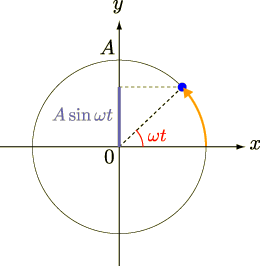
つまり,変位 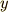 は,
は,
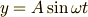
と表されることになります. 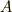 のことを「振幅」,
のことを「振幅」, 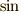 の中身(ここでは
の中身(ここでは 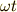 )のことを「位相」と呼びます.
)のことを「位相」と呼びます.
速度と加速度はどのように表されるか
単振動の速度 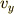 と単振動の加速度
と単振動の加速度 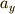 はどのようになっているでしょうか.
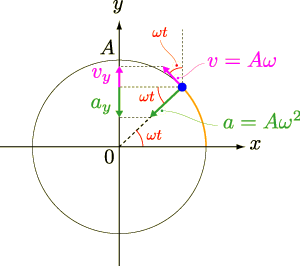
図で示すと以下のようになります.速度
はどのようになっているでしょうか.
図で示すと以下のようになります.速度  ,加速度
,加速度  を,変位と同様に
を,変位と同様に 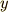 軸に射影します.
軸に射影します.
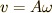 を
を 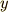 軸に射影して,
軸に射影して,
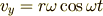
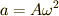 を
を 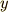 軸に射影して,
軸に射影して,
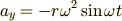
となります.また,位相の部分を 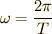 (説明は 等速円運動 を参照)を用いて,
(説明は 等速円運動 を参照)を用いて,
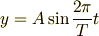
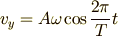
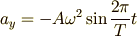
と書き換えることができます. 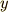 ,
, 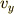 ,
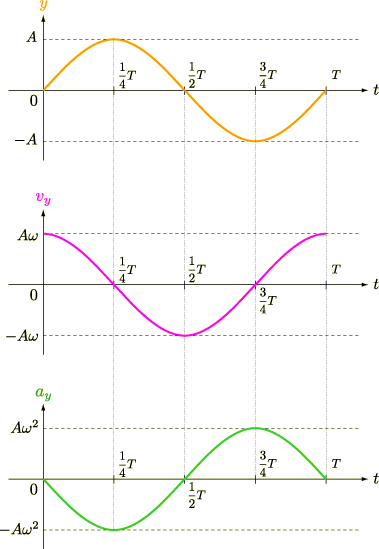
, 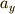 を並べてグラフに描くと以下のようになります.
を並べてグラフに描くと以下のようになります.