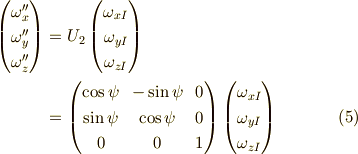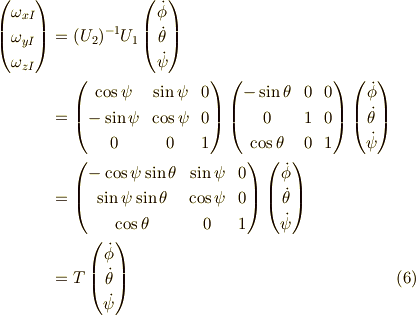剛体のオイラー角でのハミルトニアン
剛体の回転シーリズ番外編2です. オイラー角をパラメータとする剛体のハミルトニアンを求めます.
デカルト座標でのハミルトニアン
まず,デカルト座標での剛体の回転エネルギーを表す ハミルトニアンを求めます.
点  から出る角速度ベクトル
から出る角速度ベクトル  をもつ,
位置
をもつ,
位置  にある剛体
にある剛体 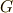 の微小要素
の微小要素 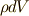 が,
寄与する角運動量は,
が,
寄与する角運動量は,
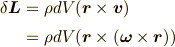
です.ここで, 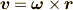 を使いました.
を使いました.
角運動量は全体で
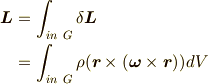
の角運動量を持ちます.
剛体  の運動エネルギー
の運動エネルギー  を考えると,
を考えると,
![H &= \frac{1}{2} \int_{in\ G} \rho \bm{v} \cdot \bm{v} dV \\&= \frac{1}{2} \int_{in\ G} \rho (\bm{\omega} \times \bm{r} ) \cdot (\bm{\omega} \times \bm{r} )dV \\&= \frac{1}{2} \int_{in\ G} \rho \bm{\omega} \cdot (\bm{r} \times (\bm{\omega} \times \bm{r})) dV \\&= \frac{1}{2} \bm{\omega} \cdot [ \int_{in\ G} \rho \bm{r} \times (\bm{\omega} \times \bm{r}) dV ] \\ &= \frac{1}{2} \bm{\omega} \cdot \bm{L}](./e78b367b6c688fe8c1164926460e53cb.png)
ここで 慣性モーメント の記事の 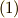 式より,
式より,
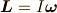
(ただし,Iは慣性テンソル)
だったので,結局運動エネルギー 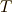 は
は

(ただし,添え字 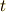 は転置を表す)
となります.
は転置を表す)
となります.
慣性主軸
デカルト座標系 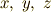 において,主慣性モーメント
において,主慣性モーメント 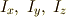 を持つ剛体があるとします.
目的は,オイラー角をつかった座標系を慣性主軸を使った座標系に対応付けることです.
を持つ剛体があるとします.
目的は,オイラー角をつかった座標系を慣性主軸を使った座標系に対応付けることです.
まずは,慣性主軸 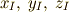 へ移る座標系を考えていきます.
へ移る座標系を考えていきます.
基底の変換の際,ベクトルの基底 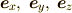 の変換行列
の変換行列 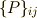 と
ベクトルの成分
と
ベクトルの成分 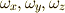 の変換行列
の変換行列 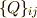 との間には,
との間には,

の関係があり,

と,

が成り立つことを確認してください [*] .
| [*] | この事については,詳しくは ベクトルの基底の変換 を参照してください. |
まずは,基底の変換を考えます.
基底 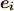 から
から 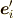 への変換は,
への変換は,

(◎は画面手前に向かうベクトル)
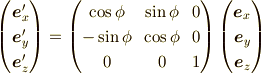
同様にして,

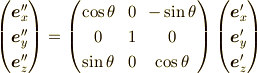

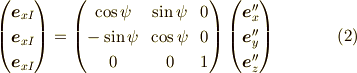
オイラー角の角速度ベクトルの導入
ここで,角速度ベクトル 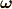 をオイラー角の角速度ベクトルの成分
をオイラー角の角速度ベクトルの成分 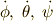 で表し,慣性主軸との対応付けすることを目的とします.ベクトルの「基底」の変換か,ベクトルの「成分」なのか注意してみてください.
「基底」
で表し,慣性主軸との対応付けすることを目的とします.ベクトルの「基底」の変換か,ベクトルの「成分」なのか注意してみてください.
「基底」 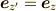 周りの回転は,
周りの回転は, 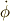 という角速度ベクトルの「成分」が対応します.
同様に
という角速度ベクトルの「成分」が対応します.
同様に 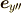 周りの回転は
周りの回転は 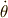 ,
,  まわりは,
まわりは, 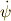 が対応します(下図参照).
が対応します(下図参照).

(上図をさらに 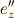 軸まわりに
軸まわりに 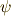 だけ回転したものが,慣性主軸
だけ回転したものが,慣性主軸 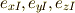 です.)
です.)
基底 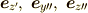 から,
から,  への変換を
もとめることができ,それは「基底の変換」として,,
への変換を
もとめることができ,それは「基底の変換」として,,
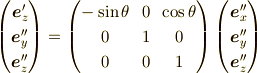
と求まります.よって,これを「成分」に直すと,
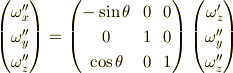
これがベクトルの「成分」の変換則です. 今,

というベクトルの成分に関する関係がありますから,
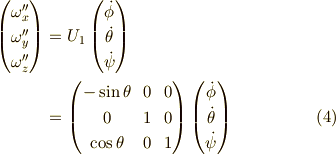
となります.
回転の運動エネルギーの表現
式  と式
と式  より,
より,
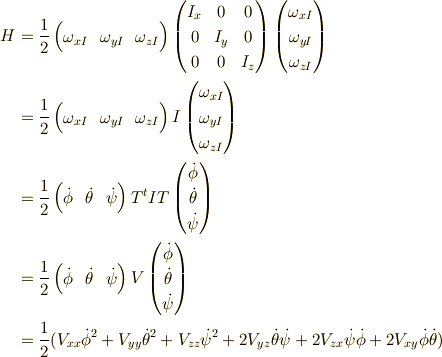
(ただし,Vは対称行列)
正準な運動量は,ハミルトニアンとパラメータ  を使って,
を使って,
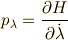
のように表わされるので,

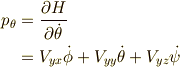

よって,

となるから,ハミルトニアンを正準な運動量で表すと,
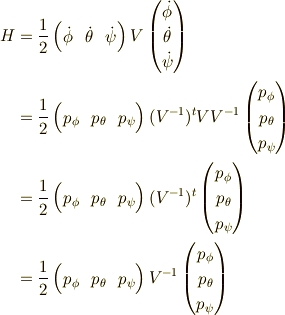
これで, 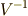 を求めればハミルトニアンが求められます.
を求めればハミルトニアンが求められます.
VとV^{-1}の計算
まず, 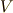 を求めます.
以前私が書いた行列の 三連続積の展開 を利用すれば,
を求めます.
以前私が書いた行列の 三連続積の展開 を利用すれば,
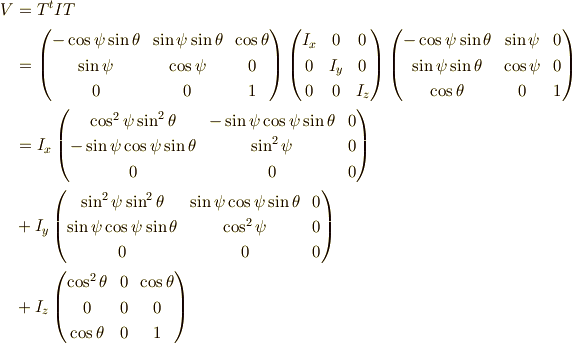
この行列の行列式は,
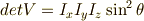
余因子行列  (逆行列の
(逆行列の 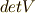 倍)の成分は,
倍)の成分は,
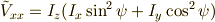

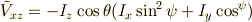
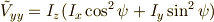
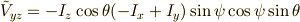

よって,無事ハミルトニアンは求まり,
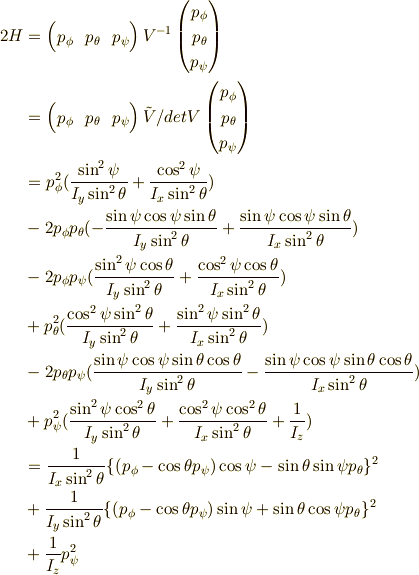
以上で終わりです. 長くなってしまったので結論だけ書くと,
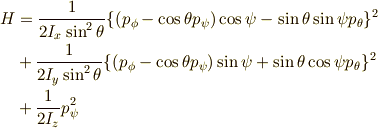
となります.
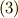 の角速度ベクトルと,
慣性主軸との対応ですから,式
の角速度ベクトルと,
慣性主軸との対応ですから,式 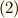 を「成分」
の変換に直すと,
を「成分」
の変換に直すと,