剛体ってなんだろう?
力学のカリキュラムとして,まず質点の力学を学び,剛体の力学へ進むというのが一般的な順番のようです.勉強を始めるまえに,剛体とはいったい何なのか?剛体の力学と質点の力学の違いは何なのか?剛体の力学に特徴的な現象にはどんなものがあるのだろうか?ということを大雑把に知っておくと,全体の見通しがよくなり,理解の助けになると思います.この記事では,剛体の力学の概論として,大事な概念やトピックを大雑把に紹介します.
剛体の定義
剛体とは,決して変形しないような,大きさのある物体のことです.

読者のみなさんの多くは,既に質点の力学の勉強をしたことがあると思います.質点というのは『大きさのない,質量だけある点』のことでした.それに対し,剛体には大きさがあります.これが一番大事な違いです.そして,決して変形しない堅い物だと考えます.剛体とはそんなものです.
実際に存在する物体は,どんなに堅いものでも,曲がったり,ねじれたり,凹んだり,割れたり,溶けたりします.そういう意味で,剛体とは一つの近似的な状態だと言えます.それでも,十分に堅い物体に対しては,この近似が役立つのです.
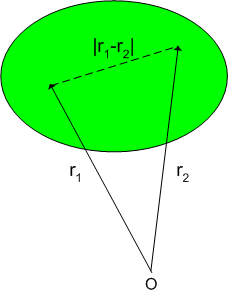
決して形が変わらないというということを,数式を使って書くこともできます.剛体内部の座標を,位置ベクトルで表すことにすると,剛体内部の異なる二点の距離は,図のように位置ベクトル 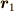 と
と 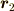 の差として表現できます.物体が剛体であることの必要十分条件は,物体内の任意の二点
の差として表現できます.物体が剛体であることの必要十分条件は,物体内の任意の二点 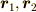 に対して,式(1)が成り立つことだと言えます. [*]
に対して,式(1)が成り立つことだと言えます. [*]

| [*] | なにもわざわざ数式で書かなくたっていいじゃないか,という声が聞こえて来そうです.『変形しない』という条件は,直観的に非常に理解しやすいものですので,何も数式にして,分かりにくくすることはありません.ところで,この記事の後半で触れますが,力学には拘束条件というものがあります.自由な運動を,何らかの形で拘束する条件がある場合に,それを拘束条件と呼ぶわけですが,剛体を無限個の質点の集まりだと考えたときに,剛体を剛体たらしめている拘束条件とは,質点同士の距離が変わらない,ということであり,その拘束条件は式(1)のように書けるのです.拘束条件を式で表わしてみるという文脈においては,このような言葉で言えば当たり前のような条件を,数式化してみることも大事です.数式で書いてみる練習だと思ってください. |
剛体の力学で重要な概念
では,剛体の力学を勉強する上で大事な概念には,どんな話題があるのでしょうか.このセクションでは,特に幾つかの大事なものを紹介します.
重心
剛体には大きさがありますので,全体の質量を代表する点として,重心を考えることが出来ます.重心とは,その一点で剛体を支えたときに,うまく釣り合うような点のことです.

剛体が何も拘束を受けておらず, 自由に運動できるとき,剛体は重心回りに運動します. (下の方に拘束条件というセクションがありますので,拘束とは何かということは,そちらをご覧下さい.回転運動については,すぐ次のセクションで説明します.)
つまり,並進運動(まっすぐな速度を持つ運動)に関しては,剛体の運動を,重心に置かれた質点(質量は剛体に等しいとします)の運動に置き換えて考えることができます.そのため,質点の力学で勉強した色々な法則(運動方程式,運動量保存則,エネルギー保存則など)が,重心に関してそのまま全て成り立ちます. [†]
また, 剛体が自由な回転運動をしているとき,剛体は重心を中心に回っていると考えることができます.つまり 自由な回転運動では,回転軸が重心を通る ということです.
| [†] | 並進運動と回転運動という言葉に慣れていないと,少しピンと来ないかもしれません.物体が,全体として,ある速度を持っているとき,これを並進運動と言います.一方,場所を変えずに,その場で自転するような運動を回転運動と言います.質点の力学に出てきた運動は,全て並進運動です.一般に,剛体は並進運動と回転運動とを合成したような運動をしますが,この二つを別々に計算することが出来ます. |
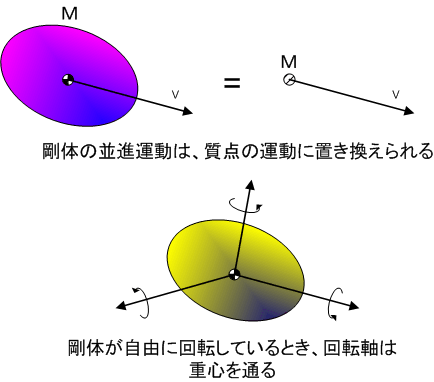
重心は,とにかく剛体の運動の中心なのです.そのため,重心を原点とする座標系で剛体の運動を考えることがよくあります.とにかく,重心は大事です.
回転運動
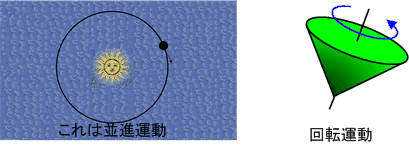
回転運動というのは,質点の力学では考えなかったものです.剛体には大きさがありますので,回転運動を,並進運動とは別に考えなければなりません. [‡]

| [‡] | 回転運動と言うのは,前のセクションの註でも触れたように,クルクルと自転する運動のことです.コマの回転を想像してみてください.それに対し,地球が太陽の周りを公転するように,何かの周りを大きく一週する運動のことを,一般に回転運動とは言いません.これは,並進運動の軌道が閉曲線になっているだけで,運動の瞬間瞬間を見れば,並進運動だからです.日常の日本語では,このような運動も回転と言ってしまいますので,混乱する人がいるかもしれません.物理で,回転運動と言ったら,自転のことです. |
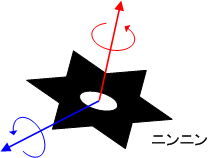
厄介なのは,回転軸の方向によって,剛体にはよく回る方向と,回りにくい方向とがあるということです.例えば,手裏剣を投げる場合を想像してみましょう.実際,手裏剣を投げたことはありませんが,おそらく,図で赤い矢印で示したような回転(つまり,手裏剣を含む平面内での回転)をしながら飛んでいくのではないでしょうか. [§] 青い矢印で示した方向に回転し続けるのは,難しそうです. 剛体にはよく回る方向と,回りにくい方向がある ということを覚えておいて下さい.
回転運動を記述するのには,回転の運動方程式というものが出てきます.少しだけ,回転の運動方程式にも触れてしまいましょう.並進運動の運動方程式 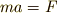 と同じ形で,
と同じ形で, 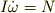 という式が成り立ちます.並進運動の力
という式が成り立ちます.並進運動の力 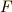 ,質量
,質量 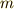 ,加速度
,加速度  に相当するのが,回転運動ではそれぞれ,トルク
に相当するのが,回転運動ではそれぞれ,トルク 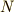 , 慣性モーメント
, 慣性モーメント 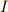 ,角速度
,角速度 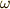 です.この慣性モーメントというのが,先ほど触れた 物体の回りにくさ を表す量です.
です.この慣性モーメントというのが,先ほど触れた 物体の回りにくさ を表す量です.
式の細部は,他の記事で,より詳しく説明される予定ですので,ここでは『回転運動には,並進運動に似たような式がなりたつんだ!』と,思っておいて下さい.剛体の力学での計算のメインは,回転運動だと言っても過言ではありません.(やや過言かも..)ブーメラン,コマ,人工衛星の運動などは,試験によく出る話題でもあります.頑張りましょう.
| [§] | 手裏剣を,人のいる方に向かって投げてはいけません. |
向きと座標変換
剛体には大きさがあるということでした.また,回りやすい方向や回りにくい方向があるということでした.そこで,剛体の幾何学的な形状や,回りやすさの方向などによって,剛体の向きというものを,決めることが出来そうです.
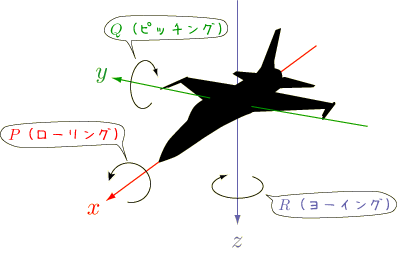
例えば飛行機を例に取りましょう.飛行機には,羽根の一部に動くような部分がありますが,全体として考えれば,あまり曲がったり割れたりするものではありませんので,剛体だと近似して運動を計算することが出来ます.
まず,幾何学的な形状を考えて,機体の対称軸に沿って上の図のように座標を取るのが自然でしょう.このように,剛体には,幾何学的な対称性などにより, 向きを決めることが出来ます. 物体が,どっちを向いている,とか言うことが出来るわけです.(飛行機を例に取りましたが,飛行機はいつも機首に向かって飛んでいるわけではありません.飛行速度(運動の向き)と,機首(幾何学的形状の向き)は全く別のものであるというのも大事な点です.)剛体の向きを考えるために, オイラー角 という3つの角度を使って,行列の計算をするのが一般的です.これは3次元での回転行列を3つ組み合わせたものですので,行列の計算が苦手な人は,回転行列というあたりを復習してみてください.
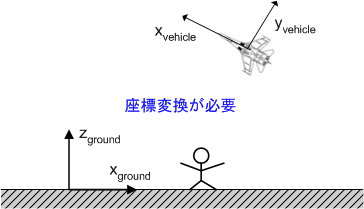
また,目的地までの距離,高度などは地上に固定した座標系(管制官の視点)で考えたほうが便利ですし,飛行機の運動は飛行機の座標系(パイロットや自動操縦装置の視点)で考えなければなりません.飛行機が空中でどんな姿勢を取ろうとも,重力は飛行機の姿勢にお構いなく,常に鉛直下向きにしか働きませんので,重力を飛行機の座標系で考えるには,適切な座標変換が必要になります.
これは一つの例ですが,剛体の運動では,往々にして 適切な座標系に座標変換する必要がある のです.これから剛体の力学には,座標変換がばんばん出てきます.ちょっと苦手だという人は,座標変換の復習をしておくのが良いと思います.
拘束条件
剛体の運動を実際に解く場合に,拘束条件が大事である場合が少なくありません.必ずしも,いつも拘束条件があるというわけではありませんが,質点の力学のときには,あまり出てこない概念でしたので,特に強調しておきます.
よくあるのは,剛体が転がるときに『滑らないように転がる』という非滑り条件です.
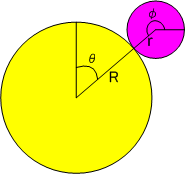
例えば,上図のように,半径 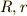 の二つの円盤が,滑らずに回転し,それぞれ角
の二つの円盤が,滑らずに回転し,それぞれ角 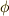 ,
, 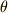 だけ回転したとします.このとき『滑らない』という条件は,『接触地点での速度が同じ』と言い換えることが出来ますので,次の式が成り立つ必要があります.
だけ回転したとします.このとき『滑らない』という条件は,『接触地点での速度が同じ』と言い換えることが出来ますので,次の式が成り立つ必要があります.
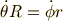
慣れていないと,ピンと来ないかも知れません.大丈夫です.これから慣れて行きます.
大事なのは,運動方程式,運動量保存則,角運動量保存則などの,一連の運動に関する微分方程式をいくらいじくっても,拘束条件の式は出てこないという点です.拘束条件というのが,こう言った物理法則の式とは違い,問題の幾何学的構成から要請される別種の条件だからです.しかし,拘束条件を忘れると,式が足りなくて問題が解けません.慣れないうちは,気がつきにくいものですので,いつも気をつけるようにしてみて下さい.
また,紐がついていたり,壁があったりして,剛体が重心以外の点を中心にして回転することがあります.このとき,回転の式や慣性モーメントの取り扱いが少し変わりますので,注意が必要です.
まとめ
剛体の問題を考えるときに必要な道具を,もう一度まとめておきます.
- 重心
- 並進運動の式 (運動方程式,運動量保存則,エネルギー保存則)
- 回転運動の運動方程式 (回転の運動方程式,角運動量保存則,回転運動のエネルギー保存則.慣性モーメント を求める計算も必要.)
- 座標変換
- 拘束条件
二番目は質点の力学と同じものです.座標変換や拘束条件,角運動量などは,剛体の力学に限ったものではありませんが,とりわけ剛体の力学の計算によく出てくるものですので,強調しておきました.
剛体の力学には,質点の力学には出てこなかった,いろいろな面白い話題があります.このサイトを通じて,剛体の力学の楽しさや奥深さを紹介することを目指します.