持ち上げるのに必要な力の大きさ
こんなことを考えてみてください.
いま重力加速度を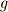
と書くことにします. そして質量
[kg] の物体を手で持って,ある高さに静止させておきましょう. さてこのとき,手が物体に加えている力の大きさはどれだけでしょうか?
考えていただけましたか?
はい.答えは 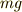 [N] ですね.
[N] ですね.
それではもう1問.
その物体を,その位置からさらに少しだけ持ち上げることにしましょう. そのとき手が物体に加える力の大きさは,どれだけでしょうか?
ええ.
これも答えは, 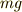 [N] です.
[N] です.
ちょっと待ってよ! 静止させておくときの力 の大きさと, 持ち上げるときの力 の大きさが, どうして一緒なの?! と思った方へ,この解説記事を贈ります.
結論から
なにか矛盾したものを感じるかも知れませんが,矛盾はありません.
質量 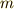 [kg] の物体を持ち上げるのに必要な力
[kg] の物体を持ち上げるのに必要な力 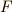 [N] は,
[N] は,
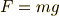
です. もちろん,この値より大きければ物体の位置を上昇させることが可能ですから,
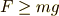
と書いても構いません.
だけど 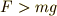 は必ず要るってわけじゃない.
は必ず要るってわけじゃない.
持ち上げるのに 必要最小限の力 というのは 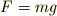 なのです.
なのです.
まず持ち上げるときの仕事について考えてみよう
持ち上げる必要最小限の力について考えるために,まずはある高さから 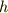 [m] 持ち上げるときの仕事を計算してみましょう.仕事は
[m] 持ち上げるときの仕事を計算してみましょう.仕事は
(力)×(移動距離)
と計算するのでしたね.
答えを先に書いてしまえば,質量 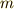 [kg] の物体を
[kg] の物体を 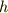 [m] 持ち上げるときに必要な仕事
[m] 持ち上げるときに必要な仕事 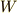 [J] は,
[J] は,
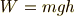
です.
これまた 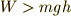 ではありません.
このことをじっくり確認してみましょう.
ではありません.
このことをじっくり確認してみましょう.
行き過ぎないように,持ち上げる
物体には 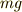 [N]の重力が働いているので,上向きの速度を持たせるためにまずは
[N]の重力が働いているので,上向きの速度を持たせるためにまずは 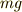 [N]より大きな力で上向きに押し上げる必要がありそうです.もしも上向きの力が
[N]より大きな力で上向きに押し上げる必要がありそうです.もしも上向きの力が 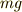 [N]より小さかったら,下向きの速度が増す(=上向きの速度が減る)ことになるでしょう.
[N]より小さかったら,下向きの速度が増す(=上向きの速度が減る)ことになるでしょう.
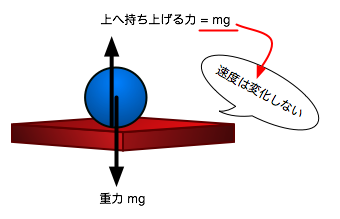
ここでは具体的に,上向きに加える力を 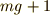 [N]だとしましょう.
上向きの力が
[N]だとしましょう.
上向きの力が 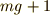 [N]であれば,下向きの重力
[N]であれば,下向きの重力 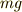 [N]と合わせて,差し引き上向きに1[N]の力がかかることになります.そのため,物体には
[N]と合わせて,差し引き上向きに1[N]の力がかかることになります.そのため,物体には 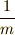
![\mathrm{[m/s^2]}](./40062bd7d07c1bfd991aba6957f07392.png) の加速度がかかって,上向きに速度が増え続けます.
の加速度がかかって,上向きに速度が増え続けます.
そのまま力を加え続けると,どんどん速さが増していって, 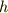 [m]持ち上がった位置を通り過ぎて,どこまでも上昇をし続けるでしょう.
だけどいまは 必要最小限の労力で,この物体を動かす ことを考えたい.
だから
[m]持ち上がった位置を通り過ぎて,どこまでも上昇をし続けるでしょう.
だけどいまは 必要最小限の労力で,この物体を動かす ことを考えたい.
だから 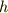 [m] 持ち上がった位置で,ちょうど静止してほしい のです.
[m] 持ち上がった位置で,ちょうど静止してほしい のです.
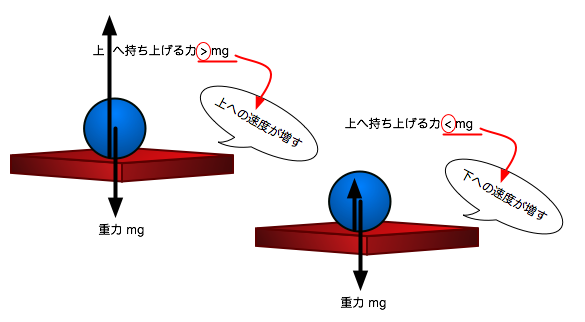
となると,持ち上げたい距離 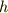 [m]の半分だけ持ち上げたところで,今度は上向きに加える力を
[m]の半分だけ持ち上げたところで,今度は上向きに加える力を 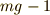 [N]に減らす必要がありますね.
そうすれば重力と差し引きして上向きに
[N]に減らす必要がありますね.
そうすれば重力と差し引きして上向きに 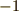 [N],つまり下向きに1 Nの力がかかって,今度は
[N],つまり下向きに1 Nの力がかかって,今度は 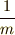
![\mathrm{[m/s^2]}](./40062bd7d07c1bfd991aba6957f07392.png) の加速度が下向きにかかることになります.
の加速度が下向きにかかることになります.
そうやればちょうど 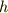 [m]だけ上がった位置で静止することになるでしょう.
[m]だけ上がった位置で静止することになるでしょう.
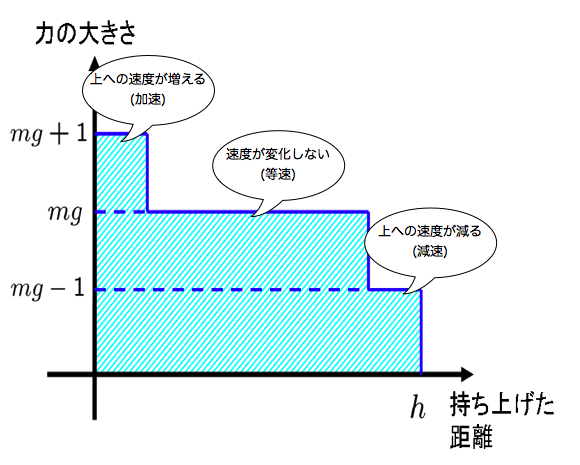
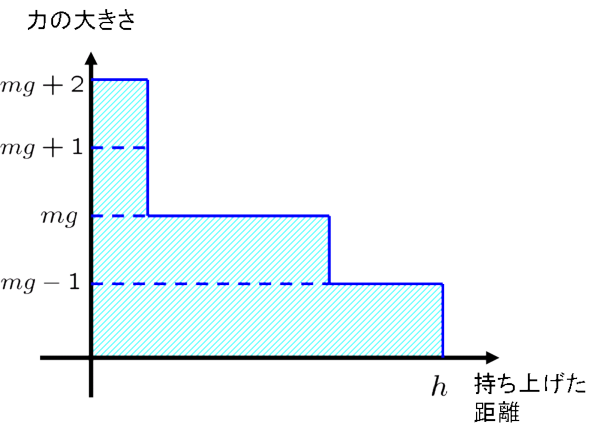
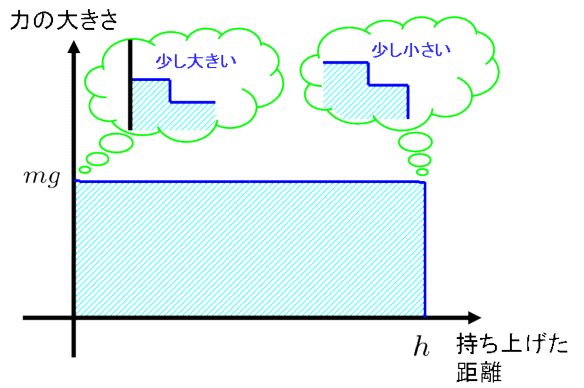
このとき,それぞれの位置でどれだけの力を加えていたのかを図で表したものが下の図です.
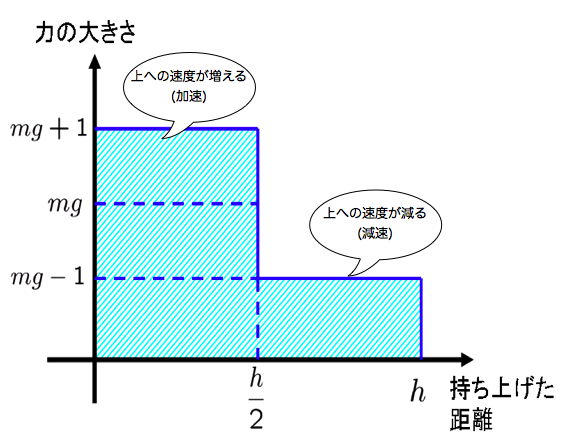
仕事というのはさっきも書きましたが,
(力)×(移動距離)
でしたね.つまり上の図で, 力の大きさと持ち上げた距離で囲まれた斜線部分の面積 の大きさが, 仕事の値 になるわけです.
計算するために,ちょっと形を整理しましょう.
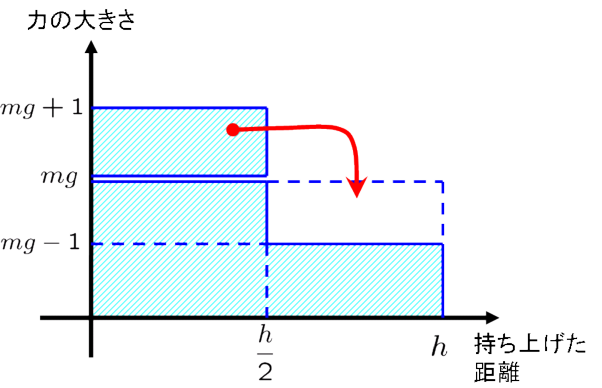
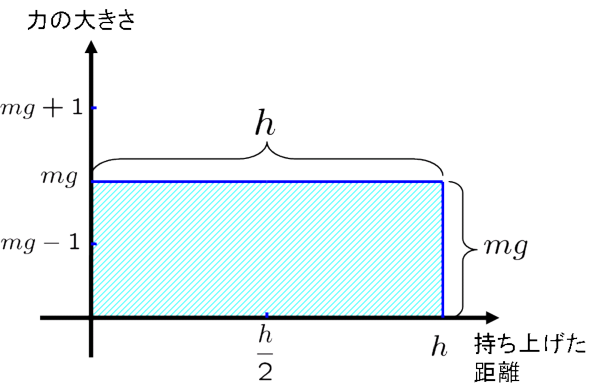
これで計算は楽になりますね.長方形の面積なので,
(面積) 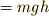 .つまり持ち上げるのに必要な最小限の仕事
.つまり持ち上げるのに必要な最小限の仕事  [J]は,
[J]は,
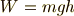
となるのです.
持ち上げ方によって仕事は変化する??
上で書いたような持ち上げ方をしたときは,確かに 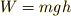 だけど,それは持ち上げ方が特別だったんじゃないの? という疑問を持つのももっともです.
だけど,
だけど,それは持ち上げ方が特別だったんじゃないの? という疑問を持つのももっともです.
だけど, 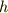 [m] 持ち上げた位置で静止 させるならば,力の加え方による影響はなく,仕事は
[m] 持ち上げた位置で静止 させるならば,力の加え方による影響はなく,仕事は 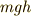 [J]となります.
[J]となります.
もう少し具体的に考えてみましょう.
さっきは半分の距離を進むまでずっと 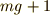 [N]の力を加えていましたが,この力を加えている時間をもっと短くしましょう.
[N]の力を加えていましたが,この力を加えている時間をもっと短くしましょう.
短い時間だけ 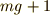 [N]の力を加えて,続いて
[N]の力を加えて,続いて 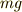 [N]の力に減らします.
そうしたら物体はどう動くでしょうか?
[N]の力に減らします.
そうしたら物体はどう動くでしょうか?
上向きの力が 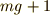 [N]から
[N]から 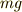 [N]に減ったから,上向きの加速度が消えます.そうなると…物体は止まる?? 違いますね. 加速度が消えたら,速度が変化しなくなる ということ.
はじめの短い時間に加速された速度のまま,上に進み続けます.
[N]に減ったから,上向きの加速度が消えます.そうなると…物体は止まる?? 違いますね. 加速度が消えたら,速度が変化しなくなる ということ.
はじめの短い時間に加速された速度のまま,上に進み続けます.
そのままの速度で進み続けたらまた目的の 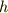 [m]を通り過ぎてしまうので,到着の直前にまた
[m]を通り過ぎてしまうので,到着の直前にまた 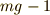 [N]の力をはじめと同じ時間(同じ距離)だけ加えることにしましょう.
そうやって,ちょうど
[N]の力をはじめと同じ時間(同じ距離)だけ加えることにしましょう.
そうやって,ちょうど 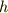 [m]持ち上げた位置で静止させます.
[m]持ち上げた位置で静止させます.
このときの仕事は?
やはり
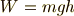
ですね.
加えている力の大きさや,力を加えている時間を調整すれば,どんな力の加え方でも同じ結果になります.
例えば最初に 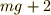 [N]の力を加えて,最後に
[N]の力を加えて,最後に 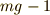 [N]の力を加えるのだとしましょう.その場合は,最初に力を加えていた間隔の2倍の距離,最後に力を加えれば良いのです.
[N]の力を加えるのだとしましょう.その場合は,最初に力を加えていた間隔の2倍の距離,最後に力を加えれば良いのです.
これでもやはり,
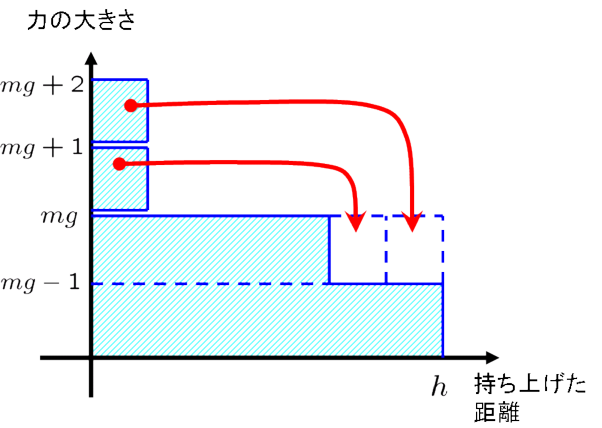
必要な仕事は 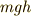 [J]となります [*] .
[J]となります [*] .
| [*] | 仕事がエネルギーに変わるという視点でも考えてみましょう.持ち上げ方に関わらず,持ち上げるための必要最小限の仕事は, 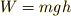 です.これは持ち上げることで行った仕事が,すべて位置エネルギーとして蓄えられるということ.もしもっと大きな力で持ち上げ続けて,仕事が です.これは持ち上げることで行った仕事が,すべて位置エネルギーとして蓄えられるということ.もしもっと大きな力で持ち上げ続けて,仕事が 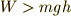 となる場合は?というと,持ち上げることで行った となる場合は?というと,持ち上げることで行った 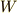 という仕事が,位置エネルギーと運動エネルギーの両方に分配されるということになります.その場合は運動エネルギーが増える…つまり,速度が増えることになります. という仕事が,位置エネルギーと運動エネルギーの両方に分配されるということになります.その場合は運動エネルギーが増える…つまり,速度が増えることになります. |
ここで遠目に見てみると…
仕事の計算結果で大事なことは,
力を加えている時間や力の大きさには関わりなく,仕事は同じである. (持ち上がった位置で静止するなら)
ということ.
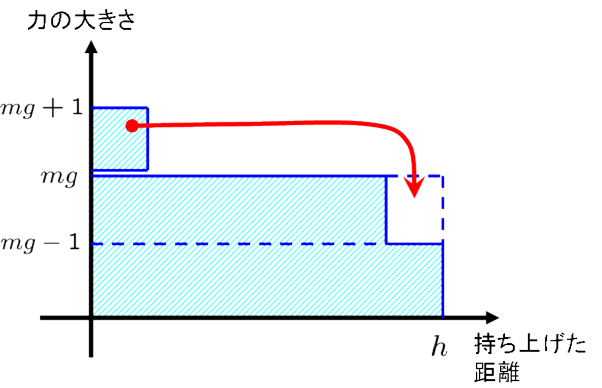
ではごく短い時間にだけ, 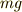 [N]より大きな力を加えていたとしましょう.さらに力の大きさは,ごくごく僅かに
[N]より大きな力を加えていたとしましょう.さらに力の大きさは,ごくごく僅かに  [N]より大きい力だとしましょう.
[N]より大きい力だとしましょう.
それを図にすると次のような感じです.
これを遠目にみると,どの瞬間でもいつも  [N]の力を加えているように見えますね.
この辺が,持ち上げる時に必要な力の大きさは
[N]の力を加えているように見えますね.
この辺が,持ち上げる時に必要な力の大きさは 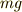 [N]だということに繋がっていきます.
[N]だということに繋がっていきます.
持ち上げるのに必要最小限の力の値は…
ここまでは持ち上げる際に行う仕事について考えてきました.そして「目的の位置まで持ち上げたら静止しているという条件を考えれば, 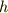 [m]だけ持ち上げるのに必要な仕事の値はつねに
[m]だけ持ち上げるのに必要な仕事の値はつねに 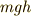 [J]になる」ということを確認しました.
[J]になる」ということを確認しました.
それでは持ち上げるのに必要な力の大きさの話に戻りましょう.
ある瞬間の力の値を求めるには…
力というのはNewtonの運動方程式に現れる量ですね. その瞬間に速度がどれだけ変化したかという量(加速度)に物体の質量を掛け算した数値が,その瞬間の力の大きさです.
そう“瞬間の”力の大きさといっても,それは速度の 変化を考えなければならない のです.“瞬間の”変化を考えるには,少しだけ時間を変化させてからその時間変化がとても少ないと考えます [†] .
| [†] | 要するに「力は微分で定義されている」ということです.数式が得意な方には 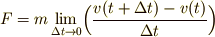 と見た方がわかりやすいでしょうか.力を定義するために,一旦,時間を有限の間隔だけ変化させてから,その変化が充分に小さいと考えていますね. と見た方がわかりやすいでしょうか.力を定義するために,一旦,時間を有限の間隔だけ変化させてから,その変化が充分に小さいと考えていますね. |
仕事の値から力を求める
力は速度の変化だと説明した直後に申し訳ないのですが,今回は力の大きさを仕事の値から求めることにしましょう.
仕事の値というのは,(力の大きさ)×(移動距離) でした. そこで, 仕事の値を移動距離で割り算して,そのときに掛かっていた力の大きさを求める ことにしましょう. ここでも“瞬間の”力の値を求めるために,わずかに“動かしたとすると…”という状況を考える必要があります. あまりにたくさん動かしたらもう瞬間の値ではありませんので,ここでも少しだけ空間を移動した場合について計算して,それからその空間間隔がとても小さいと考えることにします [‡] .
| [‡] | 再び数学が得意な方へ.ここでは力 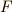 を求めるために,ある位置 を求めるために,ある位置  での仕事関数を での仕事関数を 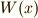 と書いて, と書いて, 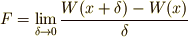 と考えているのです.ちなみにこれは,解析力学における力の定義ですね. と考えているのです.ちなみにこれは,解析力学における力の定義ですね. |
仕事の値が (力の大きさ)×(移動距離) となるのは,Newtonの運動方程式から出てきた結果です.だから速度の変化で求めた力の値も,仕事の変化から求めた力の値も,どちらも同じ値になります.
では実際に計算してみましょう
それでは,ごくごく短い距離 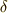 [m] だけ持ち上げたときの仕事の値を思い出してください.それは
[m] だけ持ち上げたときの仕事の値を思い出してください.それは 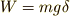 [J] でしたね.
力は仕事の値を移動距離で割り算するのでしたから,
力
[J] でしたね.
力は仕事の値を移動距離で割り算するのでしたから,
力 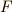 [N] はこの値を移動距離
[N] はこの値を移動距離 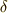 [m] で割り算して,
[m] で割り算して,
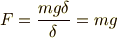
ということになります.ここの 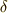 は充分に小さい値でないといけません.だから頭の中で,そう念じておきましょう(式の上では,なにも変わりませんけど).
は充分に小さい値でないといけません.だから頭の中で,そう念じておきましょう(式の上では,なにも変わりませんけど).
どんな持ち上げ方をしているのか?
さて,この持ち上げる最小限の力の値, 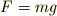 で持ち上げているというとき,どんな持ち上げ方をしているのでしょうか.
で持ち上げているというとき,どんな持ち上げ方をしているのでしょうか.
これは「どんなに短い距離であっても,行き過ぎることなく,静止することができる」という力の大きさです.
つまり いつでも止れるし,いつでも動き出せる ような力の大きさが, 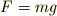 なのです.
なのです.
“瞬間の”値ってどの瞬間??
それでもまだ「動き出す瞬間は 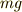 [N] より大きな力が必要なんじゃない?」と思っていますか??
[N] より大きな力が必要なんじゃない?」と思っていますか??
それは“瞬間”という言葉の使い方の問題でしょう.
動かすために,力の値がつり合いの 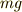 [N] から少し大きくなったとしましょう.
そのとき大きくなった後の値ではなく,大きくなる直前の値を“動き出す瞬間の”力の値と呼ぶのです.
[N] から少し大きくなったとしましょう.
そのとき大きくなった後の値ではなく,大きくなる直前の値を“動き出す瞬間の”力の値と呼ぶのです.

| [§] | 三たび数学が得意な方へ.微分の定義を思い出してください.上の図の2つの点線では便宜上,有限の時間間隔を空けていますが,微分ではその時間間隔を0の極限をとりますね.だから,2つの点線はどちらも同じ時刻を指すことになります. |
まとめ
力がつり合っている状態というのは,静止しているものは静止したまま,動いているものはその速度で動いたままという状態です. そして,止まっているものを静かに(いつでも静止できるくらいしずしずと)動かしはじめる 瞬間の 力の状態でもあるわけです.