空気抵抗がある時のモンキーハンティング
空気抵抗がある時のモンキーハンティングについて書きます.
銃弾の初期位置を原点 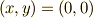 に,サルの初期位置を
に,サルの初期位置を 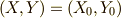 とします.
そこには一様に重力
とします.
そこには一様に重力 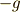 がかかっていて,空気抵抗は速度に比例してかかるものとします.
そして,サルの質量を
がかかっていて,空気抵抗は速度に比例してかかるものとします.
そして,サルの質量を 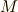 ,銃弾の質量を
,銃弾の質量を 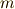 とします.
すると,サルの運動方程式は,
とします.
すると,サルの運動方程式は,

速度 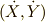 は,
は,

は良いとして,Y方向は,
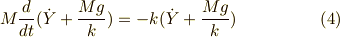
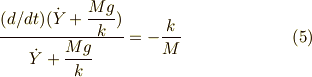
時間0からtまで定積分すると,Y方向への初期速度は0より,
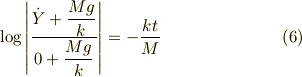
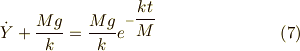
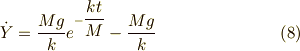
となります.
銃弾の運動方程式は,同様に解くと,初期速度 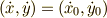 として,
として,
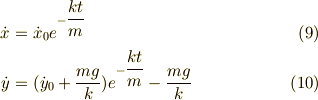
ここで,落下するサルから銃弾の速度変化を見ます.つまり,
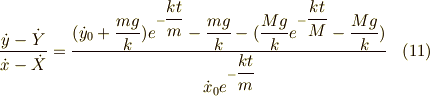
となり,よく分からない量になってしまいますが,サル,銃弾の両者の質量 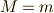 が等しいときには,
が等しいときには,
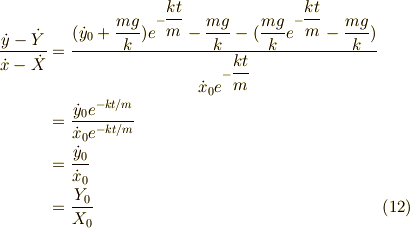
最後の等式は,銃弾の初期速度がサルの方向を向いていたということを示しています.
つまり,この時銃弾は,サルから見ると真っ直ぐに近づいてくることになり,サルに当たります.
ただし,これは銃弾は初期速度によって,一定値を超えることができないので [*] ,
銃弾の  座標が
座標が 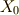 を超えることができる時です.
それでは,今日はこの辺で.お疲れ様でした.
を超えることができる時です.
それでは,今日はこの辺で.お疲れ様でした.
| [*] | 式 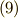 を積分すれば, を積分すれば, 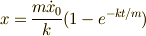 となるので,
つまりこの時,銃弾は となるので,
つまりこの時,銃弾は 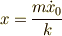 を超えられません. を超えられません. |