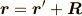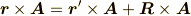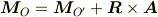ベクトルのモーメント(トルクと角運動量)
剛体の回転シーリズ第1弾です. 次の記事は, 角運動量 です.
ベクトルのモーメント
ベクトルは大きさと方向を持つ量ですが,もともと数学ではあまりその始点(どこから ベクトルを引くか)を区別することはありません.しかし物理では,同じベクトルでも その始点によって違う意味を持ったものになることがあります.例えば,物体に同じベクトル で表される力を加える場合でも,どこを押すかによって物体の動きが変わってくることは, 容易にイメージできるのではないでしょうか.
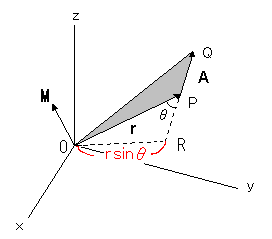
ここで,ベクトルのモーメント [*] について説明します.下の図のように,原点を
,点 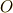 とし,位置ベクトル
とし,位置ベクトル  で表される点
で表される点 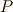 に,ベクトル
に,ベクトル
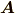 があるとします.
があるとします.
| [*] | モーメントというと,さまざまな亜種があります.力学では,モーメント(力のモーメント,トルクとも),角運動量(運動量のモーメント),慣性モーメント等があります.電磁気学では,双極子モーメント,磁気モーメント等.材料力学なんかでは,断面一次モーメント,断面二次モーメントなんていうのもあります.どれにも共通して言えるのは,ある強度と始点を問題とする位置の積で表され,採る座標系に依存している量のことのようです. |
このとき, 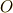 の周りのモーメントとは,
の周りのモーメントとは,
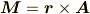
で表されるベクトル 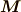 のことです.
のことです.
外積を知らない人のために少し説明しますと,
このベクトルは,  と
と 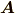 を含む平面に垂直で,大きさ
が
を含む平面に垂直で,大きさ
が 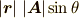 のベクトルです.
のベクトルです.
成分としては,  の成分を
の成分を 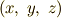 ,
, 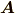 の成分
を
の成分
を 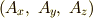 とした時,
とした時,
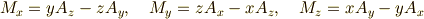
完全反対称テンソル (レヴィ・チヴィタの記号とも)を用いると,簡潔に,
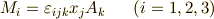
と書けます.ここで同じ添字を並べて書いたときには,すべての和をとると いうアインシュタインの縮約規則 [†] を用いています.
| [†] | 例えば 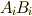 と書いたら, と書いたら, 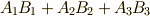 を表します. を表します. |
トルクと角運動量
特に力学では,このベクトルのモーメントの中でも重要なものとして,
トルク 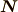 と,角運動量
と,角運動量 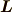 があります.物体にかかる力
があります.物体にかかる力 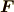 としてトルクは,
としてトルクは,
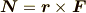
となり,角運動量は運動量 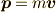 として,
として,
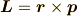
で表されます.
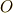 から見た点
から見た点 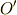 から
見た点
から
見た点 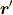 で
表し,
で
表し, 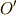 は,ベクトル
は,ベクトル 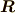 とします.
とします.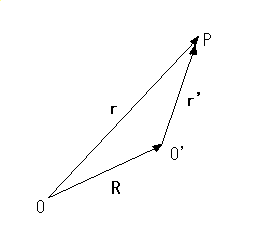
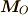 と
,
と
, 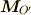 の間に次の関係が
成り立ちます.
の間に次の関係が
成り立ちます.