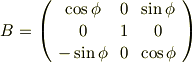無限小回転1
剛体の回転を勉強するとき,無限小回転という考え方が出てきます.回転角が無限に小さい回転を無限小回転と呼ぶのです.しかし,回転が無限に小さかったら,いつまでたっても全然回りませんね.どうして,こんな回転を考えるのでしょうか.潔く,グルリと回してしまったらいけないのでしょうか?回転について少し考察を深めてみようというのが,この記事の目的です.順序として,まず剛体の有限回転(回転の大きさが無視できない回転)について考えます.その後,有限回転と比較しながら,無限小回転に特有の特徴を考えます.このページを読み終わったら,そのまま 無限小回転2 へ進んでください.二つ合わせて一つの内容になっています.
有限回転
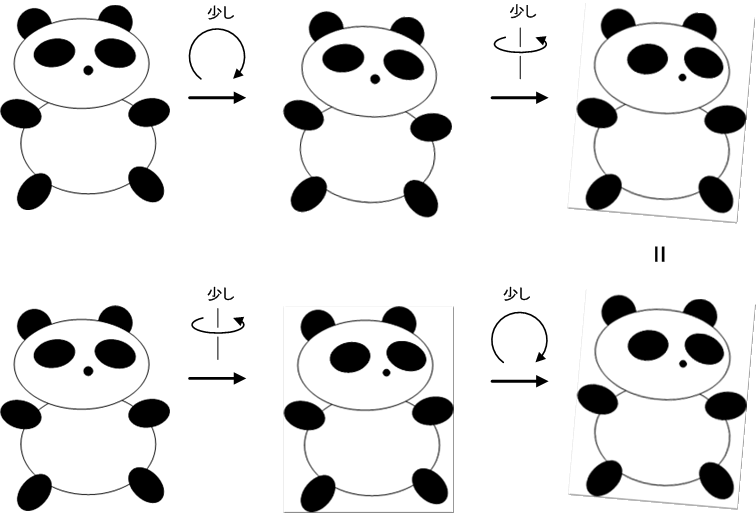
まずは次の図を見てください.剛体に,右にグルリと90度倒す回転と,180度ひっくり返す回転を連続して行った様子を描いたものです.同じ回転なのに,順序を変えただけで,結果が違ってしまっています!!
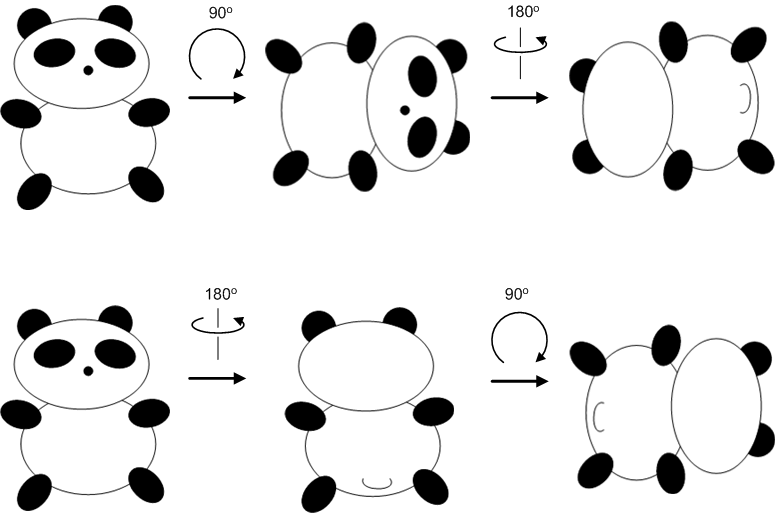
このように,回転という操作は,一般的に順序を入れ替えると結果が違ってしまうのです.順序が変えられないということを,数学では『非可換である』と言います.
剛体の向きをベクトルで表すことにすると,ベクトルに回転行列を掛けることによって,ベクトルの回転,すなわち剛体の回転を表わすことができます. [*]
では,パンダの図で行った回転を,ベクトル 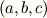 と行列を使って表現してみましょう.移動したあとのベクトルを
と行列を使って表現してみましょう.移動したあとのベクトルを 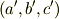 と名づけておきます.回転行列を忘れてしまった人は,この機会に 回転行列 を復習してみて下さい.とりあえず,回転行列を忘れてしまっていても,今この記事をざっと読むのには差し支えありません.
と名づけておきます.回転行列を忘れてしまった人は,この機会に 回転行列 を復習してみて下さい.とりあえず,回転行列を忘れてしまっていても,今この記事をざっと読むのには差し支えありません.
まずは,ベクトル 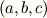 を
を 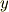 軸回りに
軸回りに 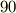 度回転させ,それから
度回転させ,それから  軸回りに
軸回りに 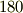 度回転させます.
度回転させます.
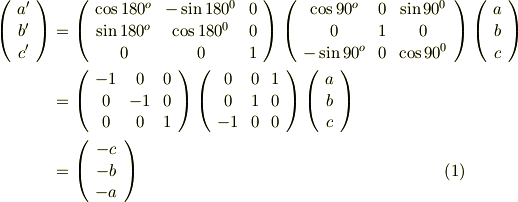
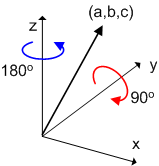
今度は先に  軸回りに
軸回りに 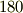 度回転させ,しかる後に
度回転させ,しかる後に 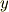 軸回りに
軸回りに 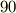 度回転させるという回転を表してみましょう.行列の順序を入れ替えただけです.
度回転させるという回転を表してみましょう.行列の順序を入れ替えただけです.
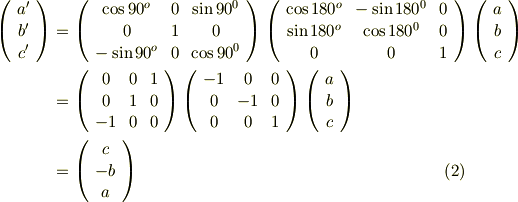
予想通り!回転の順番を変えただけで結果が違ってしまいました.数式で書くと,途端に頭が痛くなってくる人がいるかも知れませんが,どうか難しく考えないで下さい.先ほど図で見たパンダ(謎)の回転を式で表してみただけなのです.『回転は順番が大事なんだ』ということだけ頭の隅に覚えておいて下さい.細かい式は気にしなくて大丈夫です.
| [*] | 回転操作の非可換性は,行列の積が非可換である(行列 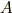 , , 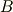 に対し,一般には に対し,一般には 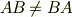 である)ことと対応しているわけです.一般に回転行列は,すべて直交行列です.直交行列とは,転置行列が逆行列になっているような行列のことでした.回転は 四元数 を用いて表現することもできます.四元数の積も,もちろん非可換になっています. である)ことと対応しているわけです.一般に回転行列は,すべて直交行列です.直交行列とは,転置行列が逆行列になっているような行列のことでした.回転は 四元数 を用いて表現することもできます.四元数の積も,もちろん非可換になっています. |
無限小回転
それでは,回転の角度が非常に小さいの場合を考えてみましょう.回転行列 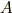 によって微小回転を表現します.
によって微小回転を表現します. 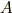 の表す回転は大変に小さいので,単位行列
の表す回転は大変に小さいので,単位行列 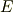 と微小回転部分
と微小回転部分  (
(  の二次以上の積は無視できる)を用いて
の二次以上の積は無視できる)を用いて 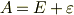 と表現できるとします.では,二つの微小回転
と表現できるとします.では,二つの微小回転  と
と  を連続して行うことを考えて見ましょう.
を連続して行うことを考えて見ましょう.
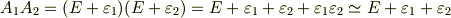
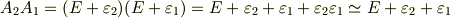
行列の積は非可換でしたが,行列の和は順番を変えても良かったことを思い出してください.(一般に行列 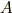 ,
, 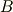 に対し,
に対し, 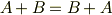 が成り立ちます.)すると,結局
が成り立ちます.)すると,結局 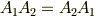 が成り立ちます.『微小回転においては,回転の順番を交換できる』と言えるわけです. [†] これはもう,回転角が大きいか小さいかというだけの問題ではありません.『可換』と『非可換』とは,数学的に,天と地ほどの違いがあるのです."無限小回転は数学的に全く違う性質を持つのだ"と思ってください.読者のみなさんにおかれましては,どうかこの感動を,しばしゆっくりと味わって頂きたいと思います.
が成り立ちます.『微小回転においては,回転の順番を交換できる』と言えるわけです. [†] これはもう,回転角が大きいか小さいかというだけの問題ではありません.『可換』と『非可換』とは,数学的に,天と地ほどの違いがあるのです."無限小回転は数学的に全く違う性質を持つのだ"と思ってください.読者のみなさんにおかれましては,どうかこの感動を,しばしゆっくりと味わって頂きたいと思います.

| [†] | 行列を微小量  で表しましたが,行列が微小とはどういうことなのか,この表記について気になった方がいらっしゃるかと思います.ベクトルに行列を掛けると,一般にはその長さと角度が変化を受けますが,ここでは行列 で表しましたが,行列が微小とはどういうことなのか,この表記について気になった方がいらっしゃるかと思います.ベクトルに行列を掛けると,一般にはその長さと角度が変化を受けますが,ここでは行列 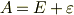 による変化が,長さについても角度についても,二次以上の項が無視できるほど微小なのだ,ということです. による変化が,長さについても角度についても,二次以上の項が無視できるほど微小なのだ,ということです. 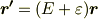 と置きますと, と置きますと, 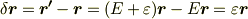 と表されますので, と表されますので, 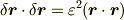 が成り立ちます. が成り立ちます. 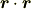 は微小量ではありませんから,結局,『ベクトルの変化 は微小量ではありませんから,結局,『ベクトルの変化 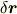 の高次の微小量が無視できる』ということを,形式的に『行列 の高次の微小量が無視できる』ということを,形式的に『行列  の高次の微小量が無視できる』と言い換えられるわけです. の高次の微小量が無視できる』と言い換えられるわけです. |
もう一度,パンダを回してみましょう.先ほどと同じ向きに回しますが,今回,回す角度をほんの少しだけにしておきます.回転の順番を変えても,結果がほとんど同じだということが見て分かります.
無限小回転を表す行列
一般に,回転という操作の順番を変えるわけにはいきませんが,無限小回転の場合に限って順番を変えても良い,ということでした.もう少し,このことの考察を進めてみましょう.
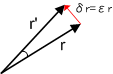
微小な回転によってベクトル  が
が 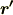 に移されたとしましょう.このとき,上の図を見れば,
に移されたとしましょう.このとき,上の図を見れば, 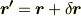 と書けることが分かると思います.
と書けることが分かると思います.
ベクトル  を
を 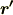 に移す変換を,行列
に移す変換を,行列 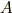 を用いて
を用いて 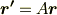 と表わすことにします.ベクトルの微小変化
と表わすことにします.ベクトルの微小変化 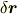 を,行列
を,行列  を用いて
を用いて 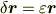 と表すことにすれば,
と表すことにすれば, 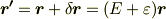 ですから,
ですから, 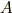 は次のように書けるでしょう.
は次のように書けるでしょう.
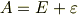
この段階では,行列  がどのような形をしているかまだよく分からないので,とりあえず成分を次のように書いておきます.未知の成分が現段階で
がどのような形をしているかまだよく分からないので,とりあえず成分を次のように書いておきます.未知の成分が現段階で 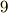 つあることを確認しておいて下さい.
つあることを確認しておいて下さい.
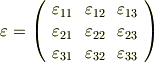
いまから行列  の形と成分を,もう少し詳しく考えてみます.道具として使うのは
の形と成分を,もう少し詳しく考えてみます.道具として使うのは  の逆行列と,
の逆行列と,  が回転を表す行列なので直交行列であるという性質の二つです.
が回転を表す行列なので直交行列であるという性質の二つです.
まず 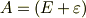 の逆行列ですが,これは
の逆行列ですが,これは 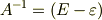 です.ちょっと天下り的ですが,確かに次のように
です.ちょっと天下り的ですが,確かに次のように 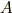 と
と 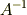 を掛け合わせてみれば単位行列
を掛け合わせてみれば単位行列 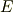 になることから確認できます.
になることから確認できます.  の自乗が無視できることに注意して下さい.
の自乗が無視できることに注意して下さい.
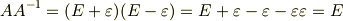
一方, 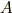 は回転を表す行列ですから,直交行列です.直交行列というのは,転置行列が逆行列になっているような行列のことを言うのでした.つまり
は回転を表す行列ですから,直交行列です.直交行列というのは,転置行列が逆行列になっているような行列のことを言うのでした.つまり 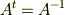 が成り立つはずです.(
が成り立つはずです.( 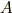 の転置行列を
の転置行列を 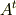 で表します.一般に行列の和と転置行列に関して
で表します.一般に行列の和と転置行列に関して 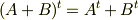 が成り立つことを使います.ここでは,証明はしませんので,よく分からない人は線形代数を復習してみてください.)
が成り立つことを使います.ここでは,証明はしませんので,よく分からない人は線形代数を復習してみてください.) 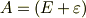 の転置行列を考えてみましょう.
の転置行列を考えてみましょう.

よって, 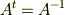 より,
より, 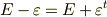 が言えます.両辺から
が言えます.両辺から 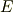 を引けば次の関係式が得られます.
を引けば次の関係式が得られます.
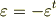
これを行列  の成分で直接考えれば,次のような関係がなりたっているということです.
の成分で直接考えれば,次のような関係がなりたっているということです.
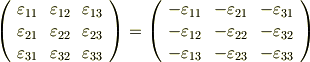
両辺の成分を一つ一つを見比べて,  の形を次のように決めることが出来ます.簡単のため,
の形を次のように決めることが出来ます.簡単のため, 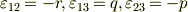 のように置きました.
のように置きました.
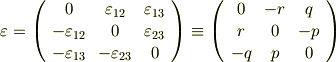
このような形の行列を反対称行列と呼びます.(  の並べ方と,マイナスのつけ方ですが,実はちょっと訳あって,このようにしました. 無限小回転2 でじきにこの理由が分かります.楽しみに待っていてください.フフフ)
の並べ方と,マイナスのつけ方ですが,実はちょっと訳あって,このようにしました. 無限小回転2 でじきにこの理由が分かります.楽しみに待っていてください.フフフ)
これは非常に感動的な結果です.一般に,3次元のベクトルに行列を作用させて有限回転を表現するには 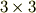 の行列が必要で,
の行列が必要で, 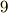 つの成分を決める必要があったわけです.ところが,微小回転ではたった
つの成分を決める必要があったわけです.ところが,微小回転ではたった 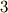 成分で済むというのですから,計算の労力が一気に三分の一に減ってしまったのです!!
成分で済むというのですから,計算の労力が一気に三分の一に減ってしまったのです!!
( 無限小回転2 へつづく)
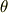 ,
,  が二次以上の項を無視できるような微小量ならば,
が二次以上の項を無視できるような微小量ならば, 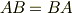 が成り立つことを確認してみて下さい.
が成り立つことを確認してみて下さい.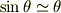 ,
, 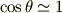 を使いましょう.
を使いましょう.