等速円運動
1つの円周上を一定の速さでまわり続ける運動を,等速円運動と呼んでいます.気象観測などに使われている 静止衛星は,地球から見ると止まっているように見えます.つまり,地球の自転と同じ速さで同じ向きに 等速円運動しているんですね.
どんな力が働くと等速円運動するだろうか
ボールを地面に置いて,足で蹴ると,蹴った方向に転がっていきます.当たり前ですね. では,その転がっているボールを,進行方向に垂直な向きに蹴るとどうなるでしょうか.
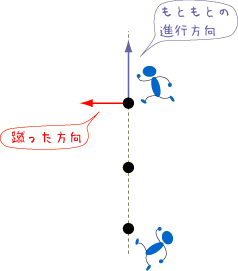
今度は蹴った方向には転がらず,下の図のように少し曲がって進んでいきます.
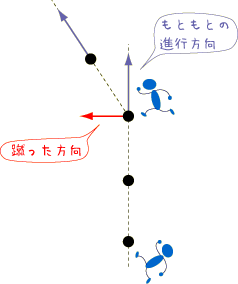
「進行方向に垂直な向きに蹴る」ということを続けていくとどうなるでしょうか.
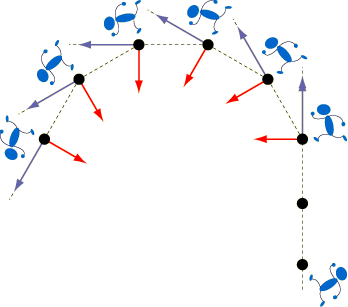
ボールは多角形の周上を運動することになります.ボールを蹴る時間間隔を短くしていけば, ボールが描く多角形は円に近づいていきますね. そして,ボールを蹴る方向は,すべてその円の中心を向く方向に近づいていくことになります. つまり,物体の進行方向(速度ベクトルの方向)に対して垂直で,1点に向かう大きさ一定の力をかけ続けると, 物体は1つの円周上を一定の速さでまわり続けるのです.これが等速円運動です. 等速円運動をしている物体にかかっている大きさ一定の力のことを「向心力」と呼びます.
等速円運動の「速さ」
物体が半径 ![r[{\rm m}]](./eac1543aeb28064123acbb2cfe638404.png) の円周上を速さ
の円周上を速さ ![v[{\rm m/s}]](./ed7b89e189472cf5e8c6bb84b1df46cc.png) で運動するとします.
円周の長さは
で運動するとします.
円周の長さは 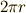 なので,物体が円周を1周するのにかかる時間を
なので,物体が円周を1周するのにかかる時間を ![T[{\rm s}]](./bd50a5d3b7c2111103b672ce1d6eeced.png) とすると,
とすると,

となります.この 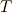 のことを「周期」と呼びます.また,単位時間(ここでは1秒)当たりに
半径が回転する角度を
のことを「周期」と呼びます.また,単位時間(ここでは1秒)当たりに
半径が回転する角度を ![\omega[{\rm rad/s}]](./291e015c30810a195188695ba772cdd9.png) とすると,
とすると,

となります.この 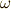 のことを「角速度」と呼びます.
(1),(2)より,
のことを「角速度」と呼びます.
(1),(2)より,

という式が成り立ちます.同じ角速度では,半径(中心からの距離)が大きいほど,大きな速さを 持つことが分かります.運動会の行進で曲がって歩いていくときに,外側の人が急がなきゃいけないのと同じことです.
等速円運動の「加速度」
等速円運動における加速度とは,どのようなものなのでしょうか. 「等速なんだから加速度は0なんじゃないの?」と思う人もいるでしょう. でも,力がかかっているわけですから, 運動方程式 を考えると,加速度は0じゃないはずです. 加速度は,「速度」の時間変化を表したものです.等速円運動では,「速さ(速度の大きさ)」は 変化しませんが,「速度」は変化しています.そう,向きが変わっているのです.
では,等速円運動の加速度 ![a[{\rm m/s^2}]](./f28640fd655d1d643122472fdc9bdb1d.png) を求めてみましょう.
微小時間
を求めてみましょう.
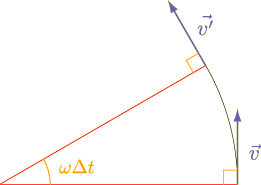
微小時間 ![\Delta t[{\rm s}]](./04a78bf52f6f8fca1f177e579049d879.png) の間に,物体は
の間に,物体は ![\omega \Delta t[{\rm rad}]](./efdcb3b6c0a21d350003c0f9e7010af4.png) だけ回転します.
このとき,速度ベクトルも
だけ回転します.
このとき,速度ベクトルも ![\omega \Delta t[{\rm rad}]](./efdcb3b6c0a21d350003c0f9e7010af4.png) だけ回転しています(速度ベクトルは半径に垂直).
初めの速度を
だけ回転しています(速度ベクトルは半径に垂直).
初めの速度を 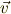 ,微小時間
,微小時間 ![\Delta t[{\rm s}]](./04a78bf52f6f8fca1f177e579049d879.png) 後の速度を
後の速度を 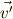 (
( 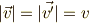 )として
図を描いてみると,以下のようになりますね.
)として
図を描いてみると,以下のようになりますね.
2つの速度ベクトルの始点をそろえて図に描いてみると,以下のようになります.
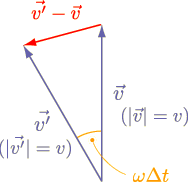
上図および 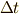 が微小であることから,
が微小であることから,
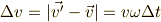
となって,
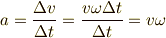
と求まります.(3)を用いると,
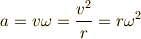
と書くこともできます. 運動方程式 より,加速度の向きは力(物体にかかる合力)の向きと同じですから, 等速円運動の場合,加速度は円の中心方向を向いていることになります.