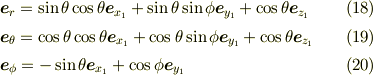角速度と速度との関係
この記事は,質点の角速度と速度との関係を幾何学的に説明するものです.2.に計算の説明を載せてありますが, これは補助的なものです.内容がどうしても理解できない場合は,2.の方から読むのも良いかと思います.
1.角速度と速度の関係について

質点が,時刻 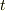 に 位置
に 位置 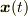 にあるとします.またこの説明では
にあるとします.またこの説明では 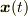 は,座標3の
は,座標3の 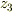 軸
上にあるものとしています(図1参照).2.の方に詳しく書いていますが,座標3とは座標1を
軸
上にあるものとしています(図1参照).2.の方に詳しく書いていますが,座標3とは座標1を 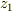 軸周りに
軸周りに  だけ回転し,
次に
だけ回転し,
次に 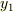 軸周りに
軸周りに 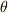 だけ回転させたものです.このときの位置
だけ回転させたものです.このときの位置 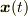 を座標3で表すと
を座標3で表すと
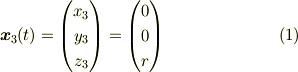
になります. 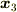 とは
とは 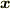 の座標3での成分表示のことを意味します.以下
の座標3での成分表示のことを意味します.以下 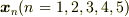 についても同じ意味で使います.
なお,速度と角速度についても同じ規約に従って書いるので,そのつもりで読んでいただきたいと思います.
次に座標3の原点から見たときの速度から,動径成分を取り除いたベクトルを
についても同じ意味で使います.
なお,速度と角速度についても同じ規約に従って書いるので,そのつもりで読んでいただきたいと思います.
次に座標3の原点から見たときの速度から,動径成分を取り除いたベクトルを 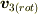 と書くとします.
すると
と書くとします.
すると 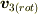 と速度
と速度 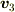 の関係は次の式で書かれます.
の関係は次の式で書かれます.
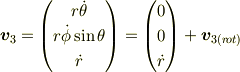
この式から 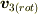 の成分が
の成分が
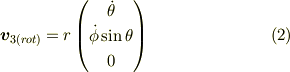
になる事が直ちに分かります.これは座標3の原点周りの回転を表す速度ベクトルで,この値は座標原点の位置に依存する量です. しかし今回の説明に限っては,全ての座標番号で原点は共通です.
ところで,ここでは角速度と速度を同時に説明するので,座標3のような軸の取り方が便利です.
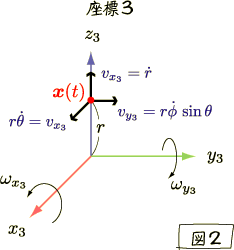
図2を見てもらうと, 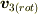 と角速度の関係はすぐに分かると思います.その具体的な関係とは,
と角速度の関係はすぐに分かると思います.その具体的な関係とは, 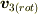 の
の 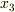 成分
が
成分
が 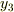 軸周りの回転,
軸周りの回転, 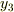 成分が
成分が 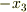 軸回りの回転を表す成分になっているというものです.
軸回りの回転を表す成分になっているというものです. 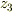 軸回りの回転は自転を意味するので,
大きさの無い質点の場合は定義することができません.以上のことから角速度の定義に従えば,角速度
軸回りの回転は自転を意味するので,
大きさの無い質点の場合は定義することができません.以上のことから角速度の定義に従えば,角速度 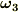 は次のようになることが分かります.
は次のようになることが分かります.
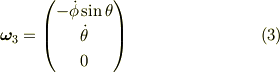
ここで座標1について,少し補足しておきます.座標1とは時刻 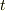 における質点の位置
における質点の位置 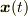 を次のような成分で表示する座標
のことで,数式で書くと次のようになります.
を次のような成分で表示する座標
のことで,数式で書くと次のようになります.

図1を見れば分かる事ですが,これはまさに任意の位置を直交座標成分で書き表したものです.
次に座標1上での角速度ベクトル 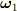 も書いておきます.
も書いておきます.
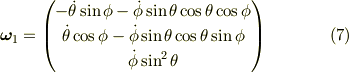
角速度の性格を眺めるには  の成分表示が役に立ちます.一方で,ある座標で任意の位置にある角速度の直交成分
を知るには
の成分表示が役に立ちます.一方で,ある座標で任意の位置にある角速度の直交成分
を知るには 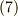 が必要です.これがここで説明したかったことの全てです.
理解できた方はさっそく下に載せてある練習問題を解いてみましょう.
が必要です.これがここで説明したかったことの全てです.
理解できた方はさっそく下に載せてある練習問題を解いてみましょう.
2.速度を求めよう
ここでは具体的な計算を示しておきます. 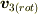 を求める方法は次の方法が考えられます.
を求める方法は次の方法が考えられます.
計算の方針
時刻
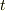 の質点の位置
の質点の位置 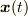 が
が 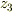 軸上にのるような位置ベクトル
軸上にのるような位置ベクトル 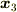 を,極座標変数
を,極座標変数 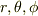 を用いて表していきます.
計算結果として,座標3上では動径方向以外の成分はゼロになることが分かるはずです.つまり,数式で書くと
を用いて表していきます.
計算結果として,座標3上では動径方向以外の成分はゼロになることが分かるはずです.つまり,数式で書くと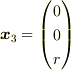
ということです.極座標変数で表すのは,動径成分と回転成分を分離して考えるのを容易にする狙いがあります.
時刻
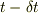 の質点の位置
の質点の位置  が
が 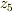 軸上に乗るような
座標5上での位置ベクトル
軸上に乗るような
座標5上での位置ベクトル 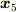 をもとめていきます.
それができたら今度は,
をもとめていきます.
それができたら今度は, 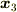 と
と 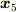 の関係式を求めることも考えます.計算結果は次のとおりです.
の関係式を求めることも考えます.計算結果は次のとおりです.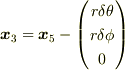
この関係式を求める狙いは,座標3上での
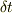 時間の微小変位量を求める事にあります.
時間の微小変位量を求める事にあります.
質点の座標3上での速度成分を微分の定義に従って求めていきます.そのときB.で求めた式を利用して,次の計算結果が得られます.
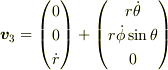
計算
ここから「計算の方針」に従って計算を進めていきます.
まず時刻 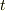 における質点の位置
における質点の位置 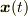 を座標1の成分表示を再掲しておきます.
を座標1の成分表示を再掲しておきます.
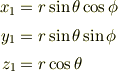
次に時刻 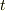 における質点の位置
における質点の位置 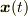 が,
が, 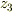 軸上になるような座標変換を実行します.この変換は
軸上になるような座標変換を実行します.この変換は 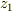 軸周りに
軸周りに  だけ回転し,
次に
だけ回転し,
次に 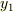 軸周りに
軸周りに 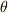 だけ回転させた変換です(図3参照).結果が
だけ回転させた変換です(図3参照).結果が 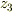 成分が
成分が  でそれ以外はゼロになる事は
計算しなくても分かります.しかし本当に考えたとおりになっているのかを調べておきます.この変換は後の計算にも利用するので,
できたら読んでいただいた方が分かりやすいかと思います.具体的な計算方法は次のとおりです.
でそれ以外はゼロになる事は
計算しなくても分かります.しかし本当に考えたとおりになっているのかを調べておきます.この変換は後の計算にも利用するので,
できたら読んでいただいた方が分かりやすいかと思います.具体的な計算方法は次のとおりです.
[計算方法]
(ア)z軸周りに  だけ回転
だけ回転
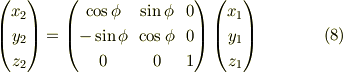
(イ) 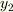 軸周りに
軸周りに 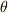 だけ回転
だけ回転
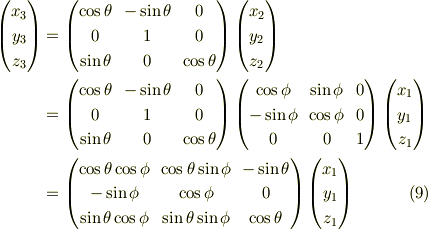
(ウ)  式に
式に  ,
, 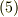 ,
,  式を代入
式を代入
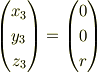
以上の(ア),(イ),(ウ)の計算を実行すれば予測された結果である 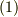 式が得られます.
これで座標3は,
式が得られます.
これで座標3は, 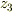 軸上に質点が時刻
軸上に質点が時刻 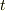 にあるような座標になることが確かめられました.
ここでもう一つ気づかなければならない事があります.それは天下り的に与えた式
にあるような座標になることが確かめられました.
ここでもう一つ気づかなければならない事があります.それは天下り的に与えた式  ,
, 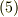 ,
,  式は
(ア),(イ),(ウ)の変換を逆にたどっていけば得られるということです.
式は
(ア),(イ),(ウ)の変換を逆にたどっていけば得られるということです.
次に時刻 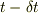 に質点が,
に質点が, 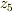 軸上に乗るような座標5上での位置ベクトル
軸上に乗るような座標5上での位置ベクトル 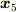 を極座標変数を用いて書き表しておきます.
この座標変換は位置ベクトル
を極座標変数を用いて書き表しておきます.
この座標変換は位置ベクトル 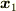 を
を 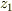 を中心に
を中心に 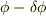 ,
, 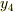 軸を中心に
軸を中心に 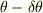 だけ回転させた変換です.
ここに書いている
だけ回転させた変換です.
ここに書いている 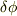 ,
, 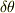 は微小な大きさの角です.
この変換は
は微小な大きさの角です.
この変換は  式を
式を 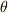 →
→ 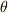

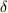
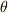 ,
,  →
→ 

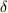
 ,
, 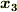 →
→ 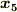 と
書き換えた式を計算する事によって求まります.
と
書き換えた式を計算する事によって求まります.

ここで三角関数の
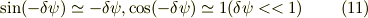
という近似を用いると
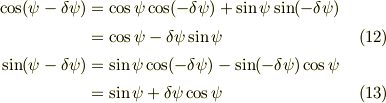
が得られます.ここで近似式を用いておりますが,微分を行うときに,切り捨てた微小量は消えてしまいます.だから計算結果に影響する事はありません. 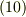 式に
式に 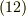 ,
, 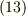 に
それぞれ
に
それぞれ 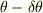 ,
, 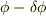 を代入したものを放り込む事によって
を代入したものを放り込む事によって
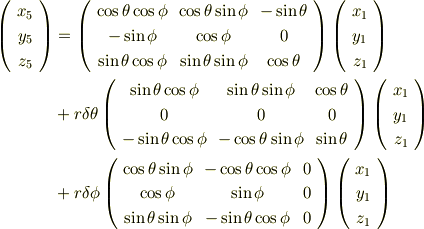
になることが分かります.更に 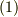 ,
, 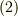 ,
, 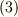 を代入すると
を代入すると
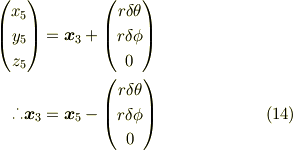
こうして 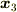 と
と 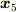 の関係を得ることができました.
の関係を得ることができました.
時刻 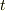 に質点は
に質点は 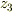 上あり,時刻
上あり,時刻 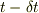 に
に 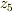 上にあります.
この位置の変位を起こす間に
上にあります.
この位置の変位を起こす間に 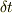 だけの時間が経過いるので,
座標3から見たときの速度
だけの時間が経過いるので,
座標3から見たときの速度 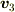 は微分の定義式から計算する事ができます.
は微分の定義式から計算する事ができます. 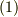 式
と
式
と 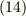 式を微分の定義式に代入してやると
式を微分の定義式に代入してやると
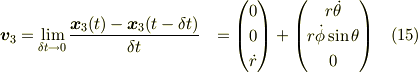
という計算結果が得られます.時刻 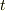 に質点は
に質点は 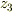 軸方向上にあるので右辺第一項は動径方向を表しています.従って動径方向成分を除いた成分が,
座標原点から見たときの回転を表す速度成分になるわけです.座標3上での
軸方向上にあるので右辺第一項は動径方向を表しています.従って動径方向成分を除いた成分が,
座標原点から見たときの回転を表す速度成分になるわけです.座標3上での 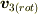 を極座標変数を用いると,
を極座標変数を用いると,  式に書かれたとおりの結果に
なります.この速度
式に書かれたとおりの結果に
なります.この速度 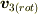 は,動径成分においてのみ速さ
は,動径成分においてのみ速さ 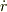 で運動する座標系から見た場合,その座標系での質点の速度になります.
読み返してもらえば分かりますが,この回転速度
で運動する座標系から見た場合,その座標系での質点の速度になります.
読み返してもらえば分かりますが,この回転速度 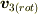 から角速度
から角速度 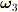 は直ちに分かります.
は直ちに分かります.
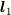 の定義式と同時に与えられる公式
の定義式と同時に与えられる公式
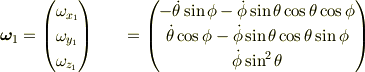

 の単位ベクトルを与えておきます(この式の導出方法を忘れた方は後で確認しておく事を勧めます).
の単位ベクトルを与えておきます(この式の導出方法を忘れた方は後で確認しておく事を勧めます).