角運動量
剛体の回転シーリズ第2弾です.前の記事は ベクトルのモーメントトルクと角運動量 です. 次の記事は, 角運動量を持つ系の例 です.
角運動量の従う式
ニュートンの力学第二法則は,
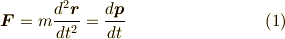
でした.
適当に座標を決めて,原点から伸びる位置ベクトルを  とします. [*] この
式の両辺のモーメントをとってみますと,
とします. [*] この
式の両辺のモーメントをとってみますと,
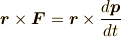
この式の左辺は力のモーメント(トルク)であり,

式 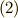 の右辺は,次に示す通り角運動量の時間微分です.
の右辺は,次に示す通り角運動量の時間微分です.
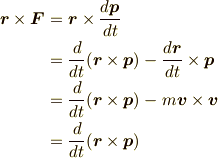
よって,角運動量とトルクの関係

が導かれるわけです.
この式 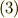 は重要ですので覚えておいてください.
は重要ですので覚えておいてください.
| [*] | ここからは原点周りの角運動量を考えていきます.別に原点まわりの角運動量以外を考えてもいいのですが,その際には前の記事で扱った平行軸の定理にしたがって値が変わってくることを覚えていてください. |
角運動量保存の法則
いま導いた式 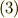 のトルクがゼロの時,角運動量は保存量になります.
式
のトルクがゼロの時,角運動量は保存量になります.
式 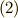 を見れば,
を見れば, 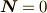 となるのは
となるのは 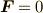 の時か,加わる力が
の時か,加わる力が  に平行なときです.
特に後者の時,働く力のことを中心力といいます.
に平行なときです.
特に後者の時,働く力のことを中心力といいます.
今,  と
と 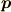 が
が 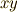 平面内にあるとき,この中心力が働いていたとします.
この時角運動量は
平面内にあるとき,この中心力が働いていたとします.
この時角運動量は  軸方向にあり,
軸方向にあり,  軸方向単位ベクトルを
軸方向単位ベクトルを 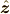 とすると,
極座標を用いて,
とすると,
極座標を用いて,
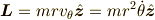
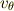 は,速度
は,速度 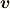 の
の 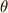 方向成分です.
角運動量ベクトルは中心力なので保存しますから,最初の値から変わらず運動中一定です.
方向成分です.
角運動量ベクトルは中心力なので保存しますから,最初の値から変わらず運動中一定です.
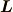 という量が面積速度という概念と結びつくことを見てみます.
という量が面積速度という概念と結びつくことを見てみます.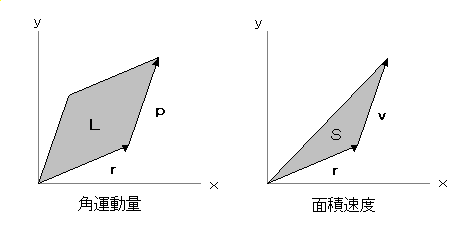
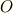 と質点を結ぶ線分が単位時間当たりに掃く面積のことで,
と質点を結ぶ線分が単位時間当たりに掃く面積のことで,
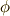 とすれば,
とすれば,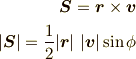
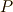 における瞬間的な面積速度と考えれば正確に一致します.
における瞬間的な面積速度と考えれば正確に一致します.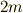 で割ってやれば
で割ってやれば 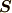 となることが分かります.
つまり,角運動量保存の法則は,面積速度は一定になることと同等であることがわかります.
となることが分かります.
つまり,角運動量保存の法則は,面積速度は一定になることと同等であることがわかります.