角運動量を持つ系の例
剛体の回転シーリズ第3弾です.前の記事は 角運動量 です. 次の記事は 全角運動量 です.
角速度ベクトル
前の記事で角運動量について学んだわけですが,それは物質の回転と
深くかかわる概念です.実際にどんな運動が角運動量を持つか見る前に角速度ベクトル
について学んでください.一応私なりにも簡単に説明しますが,
Johさんが詳しく無限小回転について書かれておられますので
もし無限小回転のもつ奇跡について感動したいという方は, ベクトルの回転 , 無限小回転1 , 無限小回転2 もご覧ください.
最後の 無限小回転2 で出てくる 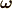 が角速度ベクトルといわれ,ここの記事で先に進む為に
必要な概念です.
が角速度ベクトルといわれ,ここの記事で先に進む為に
必要な概念です.
さて,私なりに簡単に説明します.回転には回転軸があります.回転する剛体の中の点Pの運動について考えると,
外積をよくご存知の方はわかると思いますが,回転軸に平行な単位ベクトル 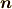 を考えれば,
回転速度方向
を考えれば,
回転速度方向  を外積
を外積 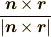 で表せます.
で表せます.
次に回転の大きさをあわせて行きたいと思います.回転の速さは,軸からの距離が遠いほど速くなりますね.
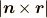 が軸からの距離を表しますから,,
これを外積
が軸からの距離を表しますから,,
これを外積 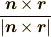 に掛けてやれば,
なんと,美しいことに
に掛けてやれば,
なんと,美しいことに 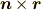 がでてきます.
がでてきます.
あとは,回転の速さを掛けてやれば速度 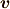 と外積
と外積 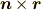 が完全に一致します.
その値とはなんでしょうか?回転の角速度
が完全に一致します.
その値とはなんでしょうか?回転の角速度 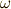 が
が 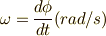 の時,軸からの距離1で点Pが
速度
の時,軸からの距離1で点Pが
速度 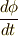 を持ちますね.一方,
を持ちますね.一方, 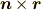 は,距離1で,大きさ1を持ちます.
は,距離1で,大きさ1を持ちます.
よって, 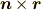 に
に 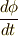 を掛けた
を掛けた 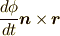 は
は
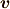 に一致します.ここで,
に一致します.ここで,
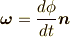
で 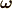 を定義すると便利であることがわかります.
を定義すると便利であることがわかります.
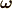 が満たす関係式として,ここで学んだように
が満たす関係式として,ここで学んだように
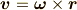
が成り立ちます. 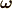 は回転軸に平行なベクトルです.
は回転軸に平行なベクトルです.
どんな時角運動量を持つの?(例1)
この記事の本題に進みます.どんな時に角運動量を持つか実例を挙げていきます. 訳あってこの記事では,xy平面内の運動しか扱いません.いまは角速度ベクトルと角運動量の方向が 一致していますが,z軸方向の運動がふくまれるとずれが生じてきます.このことは二つ後の記事で扱 おうと思います.
位置
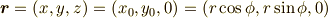
にある質量 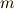 の粒子を考えます.速度
の粒子を考えます.速度
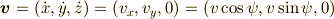
を持つとき, 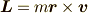 より,
より,
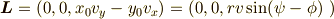
となり, z軸方向成分のみを持ちます.これはxy平面内で運動することを表します. その方向は原点に右ねじをz軸の正の方向に尖った方を向けて置いた時, 粒子の速度が動く方向にまわして,右ねじが動く方向に角運動量のベクトルは向いています. なんの力も働いていないので角運動量は保存され,一定です.
どんな時角運動量を持つの?(例2)
今度は質量の等しい反対の電荷をもつ二つの粒子が互いの引力で回転運動を起こしている 場合を考えます.回転運動ですから角運動量がz方向に成分を持てば,ああ確かに角運動量は 回転を表しているなと思えませんか?それを確かめてみます.
位置を
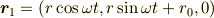
と
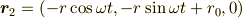
にします. 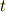 は時間です.
は時間です. 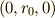 を中心に回転するモデルです.
を中心に回転するモデルです.
すると位置を 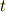 で微分すれば,運動
で微分すれば,運動 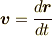 のベクトルなので,
速度はそれぞれ,
のベクトルなので,
速度はそれぞれ,
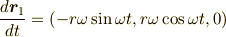
と
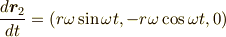
なので,それぞれの角運動量 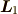 と
と 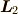 のz方向成分は,
のz方向成分は,
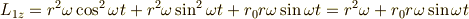
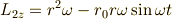
角運動量はベクトルですから足し合わせることができます.よって,z方向成分は全体として, (x成分やy成分はゼロです)
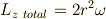
となります.これはy軸方向の位置 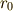 に自由度を持たせましたが,結果は
に自由度を持たせましたが,結果は 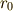 に
依りません.同様の議論をx軸にも適用できて,結局回転しあう粒子がどこにあっても
その位置に依らな
いことがわかります.モーメントとは,前の記事で書いた様にどの点に対するモーメントか
によって変動する量ですから,対になった粒子全体の角運動量がその位置に依らないことは,
回転しあう粒子系の重要な性質です.
に
依りません.同様の議論をx軸にも適用できて,結局回転しあう粒子がどこにあっても
その位置に依らな
いことがわかります.モーメントとは,前の記事で書いた様にどの点に対するモーメントか
によって変動する量ですから,対になった粒子全体の角運動量がその位置に依らないことは,
回転しあう粒子系の重要な性質です.
そして言いはぐれましたが,粒子系に働く力が内力の場合は角運動量の総和(全角運動量)
は保存します.
今回の粒子に働く力は内力のみですから,時間の変化と共に二粒子は角運動量を
やりとりしており,角運動量は全体として時間 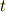 にも依らないこともわかります.
これについては,次の記事で話すことにします.
にも依らないこともわかります.
これについては,次の記事で話すことにします.
続きは こちら