加速度座標系と慣性力
剛体の回転シーリズ第6弾です.前の記事は 慣性モーメント です. 次の記事は オイラー方程式 です.
注:この記事は,「 回転する剛体上の座標 (Joh著)」とこれから書かれるであろう「見かけの力」と 同じことを扱った記事です.
加速度座標系と慣性力
あなたが巨人の指先に乗っているとします. ただし,きちんと固定されていて振り回されても落ちないようになっています.
巨人が指を振っているときに,ボールをなげてみるとどうなるでしょう. あなたにとってボールは放物線を描くことなく,複雑な軌道を描いて落ちていきます.
これはあなたが慣性座標系 [*] でなく,加速度座標系にいるために起きる現象です. このとき加速度座標系から見たボールは,重力以外の力も受けて落ちて行ったため, 複雑な軌道を描いたと考えることができます. その見かけの力を慣性力と言います.
| [*] | 慣性座標系とは,ニュートンの運動第一法則がなりたつ座標系,つまり,力を受けない物体が静止,または,等速直線運動をしつづける座標系です.一方,慣性座標系にたいして加速度運動をする座標系を加速度座標系といいます.ちなみに「座標」というと,点の位置を指定する数の組のことです. |
座標の変換
慣性力は座標の変換を数式で表すことにより求められます. ここでは,直交座標系を採用します.
加速度座標系の慣性座標系に対する運動は,二つの運動に分解できます.
ひとつは,原点の移動(座標の平行移動). もうひとつは,向きの変化(座標の回転).
原点の移動は,慣性座標系の原点を始点とした位置ベクトル [†] で記述できます. 加速度座標系から見たベクトル量を考えたとき, ベクトル量の中でも位置ベクトルのみが影響を受けます.
| [†] | 位置ベクトルとは,ベクトルの中でも特に始点を固定したベクトルで,普通座標系の原点に始点をとり位置を表すことができます. |
向きの変化は,角速度ベクトル 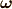 で記述できます.
ただし,一般的にはこの角速度ベクトルは時間と共に向きと大きさが変化します.
同じく加速度座標系から見たベクトル量を考えたとき,
この変化による影響は位置ベクトルを含むすべての種類のベクトルに影響します.
で記述できます.
ただし,一般的にはこの角速度ベクトルは時間と共に向きと大きさが変化します.
同じく加速度座標系から見たベクトル量を考えたとき,
この変化による影響は位置ベクトルを含むすべての種類のベクトルに影響します.
慣性座標の単位長さの基底ベクトルを,「慣性座標系」を英語にした inertial coordinate system の 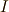 をとって,
をとって,
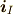 ,
, 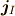 ,
, 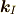 で表わします.
で表わします.
一方,加速度座標系の時間に依存して向きを変える単位長さの基底ベクトルを,
 ,
, 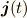 ,
, 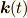 で表わします.
以下,これを略記して,
で表わします.
以下,これを略記して,
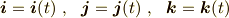
と書きます.
ここで,この空間内にあるあるベクトル  (これは位置ベクトルは除きます.
原点の位置は問題としないのです.)を考えます.すると,ふたつの座標系での表現は,
(これは位置ベクトルは除きます.
原点の位置は問題としないのです.)を考えます.すると,ふたつの座標系での表現は,
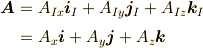
ここで,  の時間変化を見るため時間微分をとってみます.
の時間変化を見るため時間微分をとってみます.
注意するべき点は,
ひとつは,慣性座標系の基底ベクトルは変化しない為,時間微分は 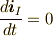 などが成立すること.
などが成立すること.
もうひとつは,角速度ベクトル  で回転する座標系では,
基底ベクトル
で回転する座標系では,
基底ベクトル  の始点がどこにあっても,
結局,時間微分は,時間変化前と時間変化後のふたつのベクトルを,
始点をそろえたときの変化量をみるので,その角度変化のみが問題となり,
いくつか前の記事 角運動量を持つ系の例 で出てきた(位置)ベクトル [‡]
の時間微分の公式,
の始点がどこにあっても,
結局,時間微分は,時間変化前と時間変化後のふたつのベクトルを,
始点をそろえたときの変化量をみるので,その角度変化のみが問題となり,
いくつか前の記事 角運動量を持つ系の例 で出てきた(位置)ベクトル [‡]
の時間微分の公式,
| [‡] | 座標の回転が加速度座標系から見たベクトルに与える影響は,それが位置ベクトルでも,ただのベクトル量でも同じなので位置にカッコを付けました. |
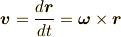
を適用できて,
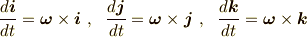
です.
よって,ベクトル  の時間微分は慣性座標系では次のようになります.
の時間微分は慣性座標系では次のようになります.
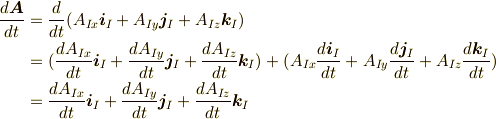
これは,普通のベクトルの微分ですね.一方,加速度座標系での微分は,
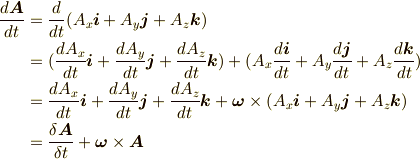
ここで,最後の行の 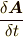 は,加速度座標系からみた時間変化速度を表しています.
は,加速度座標系からみた時間変化速度を表しています.
簡潔に書くと,
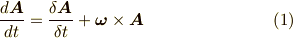
という公式が得られました.
ベクトルの時間変化は,その座標系から見た変化に,座標系自身が回転している効果(  の項)が加わります.
の項)が加わります.
加速度座標から見た運動方程式
こうして得られた式で,加速度座標系から見た運動方程式を考えてみましょう.
元となる式は,質点 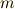 の位置
の位置 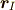 の変化に関する方程式,ニュートンの運動方程式で,
の変化に関する方程式,ニュートンの運動方程式で,

この左辺は,位置ベクトルですから,座標の原点の移動のことも考慮します.
慣性座標系から見た加速度座標系の原点の位置が 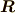 だとします.
慣性,加速度座標系から見た質点の位置は,それぞれ
だとします.
慣性,加速度座標系から見た質点の位置は,それぞれ 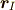 ,
,  とすると,
とすると,
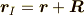
の関係が成り立ちます.二回時間微分を施すと,
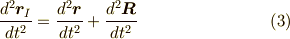
右辺第一項は加速度座標系から見た位置なので,加速度座標系から見た基底ベクトルで表わすべきで,

ここで,式  で
で  として,
として,
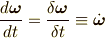
が得られます.また,
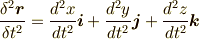
という意味です.式 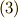 に式
に式  を代入して,
を代入して,

これと式 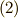 から,
から,
![m \frac{\delta^2 \bm{r}}{\delta t^2} = \bm{F} -m [\bm{\omega} \times ( \bm{\omega} \times \bm{r})+ 2 \bm{\omega} \times \frac{\delta \bm{r}}{\delta t} + \dot{\bm{\omega}} \times \bm{r} + \frac{d^2\bm{R}}{dt^2} ] \tag{6}](./8b935c291353e18af280d97b66ba1535.png)
最初の話の繰り返しになりますが,この式の意味するところは,
加速度座標系から見た質点が軌道を書くとき,そこには外力 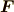 の他に,座標の変化の仕方に依存する力が働いているように
見えるということを表していて,この見かけの力のことを「慣性力」といいます.
の他に,座標の変化の仕方に依存する力が働いているように
見えるということを表していて,この見かけの力のことを「慣性力」といいます.
式 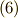 の右辺の中カッコ内の力の名前は,
の右辺の中カッコ内の力の名前は,
第一項 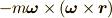 :遠心力
:遠心力
第二項 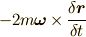 :コリオリ力
:コリオリ力
第三項 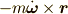 :オイラー力(座標系の回転の加減速による力)
:オイラー力(座標系の回転の加減速による力)
第四項 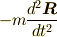 :直進力
:直進力
次の話では,回転する物体に張り付いた加速度座標系から見た剛体の回転の方程式を考えます.
続きは こちら