変分法2
変分法1 では,関数 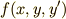 によって決まる汎関数
によって決まる汎関数 ![I[y]\equiv \int _{a}^{b}f(x,y,y')dx](./26d978851963de88325d8681d335da87.png) の停留値問題を解くためには,オイラー方程式を解けば良いのだということを勉強しました.
の停留値問題を解くためには,オイラー方程式を解けば良いのだということを勉強しました.
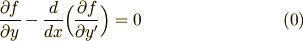
ここでは,オイラー方程式の,さらに発展的な形について勉強します.もし,なんだかちょっと難しいぞ,と感じる人は,もう一度 変分法1 を復習して下さい.
色々な関数形が出てきますが,その全てを理解する必要はありません.全部読むのは長くて大変ですから,必要なときに必要な部分だけ,この記事を参考書代わりに読んで頂ければ十分だと思います.次のセクションが目次を兼ねています.
色々な関数形
汎関数 ![I[y]](./15ed8cca5742103c5bdb7f8e11f0dfb1.png) を決める関数として, 変分法1 では
を決める関数として, 変分法1 では 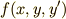 という形のものしか考えませんでした.しかし,言うまでもなく世の中には,もっと色々な形の関数があります.これよりももっと簡単な形の関数もあれば,もっと複雑なものもあるわけです.次に挙げるような関数に対して,オイラー方程式( 変分法1 で導いたオイラー方程式と区別するために,これらを変形オイラー方程式と呼びます)を導くのがこの記事の目的です.
という形のものしか考えませんでした.しかし,言うまでもなく世の中には,もっと色々な形の関数があります.これよりももっと簡単な形の関数もあれば,もっと複雑なものもあるわけです.次に挙げるような関数に対して,オイラー方程式( 変分法1 で導いたオイラー方程式と区別するために,これらを変形オイラー方程式と呼びます)を導くのがこの記事の目的です.
1.〜3.は, 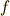 が,特に簡単な関数形をしている場合です.4.は,
が,特に簡単な関数形をしている場合です.4.は, 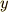 以外にも変数を含む場合です.
以外にも変数を含む場合です.  も
も  の関数であることに注意して下さい.これは一般に
の関数であることに注意して下さい.これは一般に  個の変数を含む場合に容易に拡張できますので,本文の方でその場合にも触れます.5.は
個の変数を含む場合に容易に拡張できますので,本文の方でその場合にも触れます.5.は 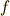 が
が 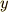 の二次導関数まで含む場合です.5.の場合を更に一般の高次導関数まで拡張したものが6.です.5.と6.は本質的に同じ問題ですが,少し計算が長くなるので別にしました.1.〜6.に出てくる
の二次導関数まで含む場合です.5.の場合を更に一般の高次導関数まで拡張したものが6.です.5.と6.は本質的に同じ問題ですが,少し計算が長くなるので別にしました.1.〜6.に出てくる 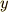 や
や  は
は  の関数でしたから,基本変数は
の関数でしたから,基本変数は  だけでした.7.として,独立に動ける基本変数が
だけでした.7.として,独立に動ける基本変数が 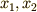 のように複数個あり,それらの関数である
のように複数個あり,それらの関数である 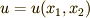 と,その偏導関数
と,その偏導関数 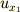 .
. 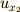 が
が 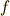 に含まれる場合を考えます.
に含まれる場合を考えます.
以下に,この7つのタイプの変分問題について,順番に変形オイラー方程式を導いていきます.本文では一応導出の過程も全て述べますが,これらを覚える必要は全くありません.最後に幾つかの例題を載せておきますので,出来れば答えを見ないでチャレンジしてみてください.
色々な変形オイラー方程式
1. 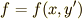
これは関数 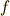 に
に 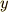 が含まれていない簡単な形です.
が含まれていない簡単な形です. 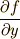 が零になりますので,オイラー方程式(0)は次式のようになります.
が零になりますので,オイラー方程式(0)は次式のようになります.
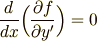
両辺を  で積分して次のような形になります.これが1番目の形の変形オイラー方程式です.
で積分して次のような形になります.これが1番目の形の変形オイラー方程式です.

とても計算が簡単だったので,なにもわざわざ勿体ぶって公式などと呼ぶ必要はないと感じた読者の方が多いと思います.しかし,実際に変分法の問題を解くときには少しでも簡単な形から始めるということが,とても重要なのです.オイラー方程式は二階微分方程式ですが,式(1)は一階微分方程式の形をしています. 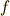 が少し複雑な形をしている場合,無駄な微分の手間を一回省くというのは非常に大きな節約になります.
が少し複雑な形をしている場合,無駄な微分の手間を一回省くというのは非常に大きな節約になります.
2. 
まず 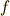 の全微分を考えます.
の全微分を考えます.
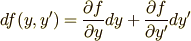
少し式変形をして,次のような形にまとめます.
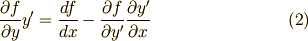
一方,オイラー方程式(0)の両辺に  を掛けたものを考えます.
を掛けたものを考えます.
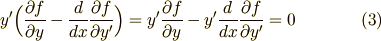
式 (2)(3)を連立して 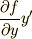 を消去します.
を消去します.

この公式は1868年にベルトラミによって導かれたので,特にベルトラミの公式という名前がついています.この公式が使える問題の中で有名なものに, 最速降下曲線 を求めるというものがあります.
3. 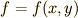
関数 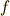 に
に  が含まれていない場合です.
が含まれていない場合です. 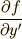 の項を落とすと,オイラー方程式(0)は次のような形になります.
の項を落とすと,オイラー方程式(0)は次のような形になります.

これは直ちに積分できて, 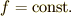 が言えるでしょう.変分問題としては,全然面白くない形の関数でした.
が言えるでしょう.変分問題としては,全然面白くない形の関数でした.
4. 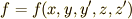
関数 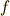 が,
が, 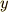 以外にも変数を含む場合です.汎関数は次式(6)のように表されます.
以外にも変数を含む場合です.汎関数は次式(6)のように表されます.
![\displaystyle I[y_{1},y_{2}]\equiv \int _{a}^{b}f(x,y,y',z,z')dx \tag{6}](./402b1b7e698ff12e36d769154dc2ce83.png)
ここで, 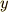 も
も  も
も  の関数であることに注意しましょう.関数形の微小な変形を,任意関数
の関数であることに注意しましょう.関数形の微小な変形を,任意関数 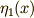 ,
, 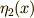 と任意の微小量
と任意の微小量  を使って,次のように表現することにします.
を使って,次のように表現することにします.
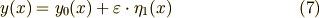
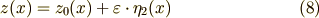
式(7)には  が含まれていませんし,式(8)には
が含まれていませんし,式(8)には 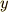 が含まれていません.そこで,式(7)(8)をそれぞれ別の変分問題だと考えることができます.これは 変分法1 で求めた形のオイラー方程式に帰着する形ですから,結果が次の式(9)(10)のように書けます.オイラー方程式が二本出てきたということです.これらを連立することで変分問題が解けます.
が含まれていません.そこで,式(7)(8)をそれぞれ別の変分問題だと考えることができます.これは 変分法1 で求めた形のオイラー方程式に帰着する形ですから,結果が次の式(9)(10)のように書けます.オイラー方程式が二本出てきたということです.これらを連立することで変分問題が解けます.
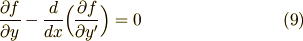
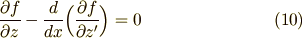
変数がたくさんある場合には,変数の数だけオイラー方程式が出てきます.一般に,関数 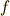 が
が  個の変数を含み,
個の変数を含み,  と表わされる場合,この
と表わされる場合,この 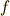 に関する変分問題は次のように,
に関する変分問題は次のように,  次連立オイラー方程式を解くという問題に帰着します.
次連立オイラー方程式を解くという問題に帰着します.
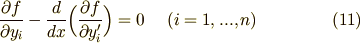
5. 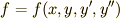
関数 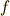 が
が 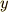 の二次導関数までを含む場合です.基本的には 変分法1 で行った計算と同じですので,そのときの手順も思い出しながら計算を追ってみて下さい.
の二次導関数までを含む場合です.基本的には 変分法1 で行った計算と同じですので,そのときの手順も思い出しながら計算を追ってみて下さい.
汎関数の形は式(12)のように書けることでしょう.また, 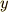 の関数形の微小な変化は,任意の関数
の関数形の微小な変化は,任意の関数 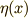 と任意の微小量
と任意の微小量  を用いて式(13)のように書けます.
を用いて式(13)のように書けます.
![\displaystyle I[y]\equiv \int _{a}^{b}f(x,y,y',y'')dx \tag{12}](./7c6b6b73cbf54c91e5f63a12f463a3f8.png)
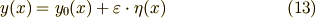
式(12)で表される汎関数  に対し,
に対し, 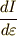 が次式のようになるというは大丈夫でしょうか.一行目では
が次式のようになるというは大丈夫でしょうか.一行目では  の全微分を考えています.一行目に出てきた
の全微分を考えています.一行目に出てきた  などを式(13)を用いて変形したのが二行目です.
などを式(13)を用いて変形したのが二行目です.
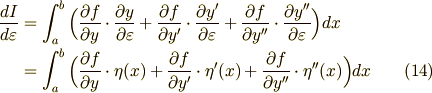
次に,式(14)の二行目の第三項を 部分積分 します.
![{dI\over d\varepsilon }&=\int _{a}^{b} \Big({\partial f\over \partial y}\eta (x)+{\partial f\over \partial y'}\eta '(x)+{\partial f\over \partial y''}\eta ''(x)\Big)dx \\&=\bigg[{\partial f\over \partial y''}\eta '(x)\bigg]_{a}^{b}+\int _{a}^{b}\bigg({\partial f\over \partial y}\eta (x)+{\partial f\over \partial y'}\eta '(x)-{d\over dx}\Big({\partial f\over \partial y'}\Big)\eta '(x)\bigg) dx \\&=0](./81e26d7b5043bc63cd7b1d6dee6fab37.png)
積分の中から 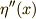 が外に出せました.もう一回頑張って,積分の中の第二項・第三項を部分積分しましょう.今度は
が外に出せました.もう一回頑張って,積分の中の第二項・第三項を部分積分しましょう.今度は  をなくすのが目標です.
をなくすのが目標です.
![&\bigg[{\partial f\over \partial y''}\eta '(x)\bigg]_{a}^{b}+\int _{a}^{b}\bigg({\partial f\over \partial y}\eta (x)+{\partial f\over \partial y'}\eta '(x)-{d\over dx}\Big( {\partial f\over \partial y'}\Big) \eta '(x)\bigg) dx \\&=\bigg[ {\partial f\over \partial y''}\eta '(x)+{\partial f\over \partial y'}\eta (x)-{d\over dx}\Big({\partial f\over \partial y'}\Big)\eta (x)\bigg]_{a}^{b}+\int _{a}^{b}\eta (x)\biggl\{ {\partial f\over \partial y}-{d\over dx}\big( {\partial f\over \partial y'}\big) +{d^{2}\over dx^{2}}\big( {\partial f\over \partial y'}\Big) \biggl\} dx \\&=0](./badebafbed3746be8d2a6652d6c2e188.png)
境界条件より,最初の括弧は全て零になります. 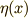 は任意の関数だということでしたから,結局,上式が成り立つためには,次式(15)が成り立つことが必要十分条件となります.これが求める変形オイラー方程式です.オイラー方程式(0)と比べてみてください.
は任意の関数だということでしたから,結局,上式が成り立つためには,次式(15)が成り立つことが必要十分条件となります.これが求める変形オイラー方程式です.オイラー方程式(0)と比べてみてください.
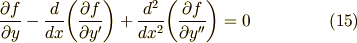
7. 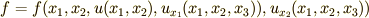
今まで見てきた関数では, 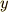 や
や  は
は  の関数でしたから,結局,一番基本的な変数は
の関数でしたから,結局,一番基本的な変数は  だけでした.ここでは,そのような基本変数が二個ある場合を考えます.このとき汎関数は次式のように書けます.重積分になっているところがポイントです.
だけでした.ここでは,そのような基本変数が二個ある場合を考えます.このとき汎関数は次式のように書けます.重積分になっているところがポイントです.
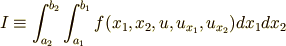
式中, 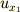 というのは,
というのは,  の
の 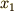 による偏微分という意味だとします.例によって,
による偏微分という意味だとします.例によって,  の微小な変化を,任意の微小量
の微小な変化を,任意の微小量  と,任意の関数
と,任意の関数  によって,次のように表しましょう.
によって,次のように表しましょう.
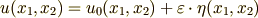
次に, 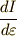 を考えます.
を考えます. 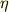 の偏導関数が二種類出てくるのがポイントです.
の偏導関数が二種類出てくるのがポイントです.
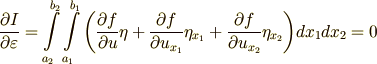
右辺の括弧内の,第二項,第三項をそれぞれ 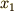 と
と  で部分積分します.
で部分積分します.
![\displaystyle \Big[\frac{\partial f}{\partial u_{x_{1}}}\frac{\partial^2 \eta}{\partial {x_{1}}^2}\Big]_{a_{1}}^{b_{1}}+\Big[\frac{\partial f}{\partial u_{x_{2}}}\frac{\partial^2 \eta}{\partial {x_{2}}^2}\Big]_{a_{2}}^{b_{2}}+\int _{a_{2}}^{b_{2}} \limits \int _{a_{1}}^{b_{1}} \limits \biggl\{ {\partial f\over \partial u}-{d\over dx_{1}}\bigg({\partial f\over \partial u_{x_{1}}}\bigg)-{d\over dx_{2}}\bigg({\partial f\over \partial u_{x_{2}}}\bigg)\biggr\} \eta dx_{1}dx_{2}=0](./75afac4e1d977433991d8350f3b7d6c2.png)
部分積分した前へ出した部分は,境界条件によって零になります.また 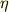 は任意の関数だということでしたので,結局,上式が成り立つための必要十分条件は,次式(17)が成り立つことです.
は任意の関数だということでしたので,結局,上式が成り立つための必要十分条件は,次式(17)が成り立つことです.
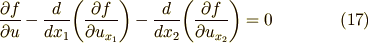
オイラー方程式(0)と見比べてみて下さい.
例題
1.[直線距離]
二点 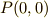 ,
,  を結ぶ最短経路を求めて下さい.
を結ぶ最短経路を求めて下さい.
解答
この答えが直線であることは直感的に明らかですが,変分法を使って解くのが練習です.二点を結ぶ任意の曲線の長さ 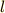 は,次のように書けますね.
は,次のように書けますね.
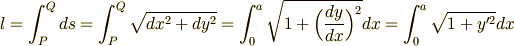
求めたいのは 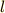 の最小値ですから,
の最小値ですから, 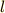 を汎関数にとり,さっそく変分法で解きましょう.
を汎関数にとり,さっそく変分法で解きましょう.
![\displaystyle I[y]\equiv \int _{0}^{a}f(x,y,y')dx=\int _{a}^{b} \sqrt{1+y'^2}dx](./a7789bea5feeb2c93cee36177dd495f4.png)
この問題では 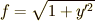 となっていますね.これは
となっていますね.これは 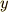 を含まない形ですから,変形オイラー方程式(2)が使える形です.求める変形オイラー方程式は次のようになります.
を含まない形ですから,変形オイラー方程式(2)が使える形です.求める変形オイラー方程式は次のようになります.
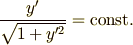
これを一回積分すれば, 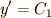 となります.もう一度積分して次の答えが得られます.
となります.もう一度積分して次の答えが得られます.
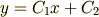
積分定数 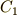 ,
, 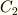 は,この直線が二点
は,この直線が二点 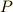 ,
, 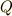 を通るという条件から決まります.予想通り,
を通るという条件から決まります.予想通り, 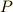 ,
, 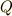 を通る直線が,最短経路だということになりました.
を通る直線が,最短経路だということになりました.
2.[最速降下曲線]
高さの異なる二点を坂道で結び,玉を転がすとき,玉が一番速く転がる坂の形(曲線)を考えてください.重力は一様だとします.
この問題の解答は, 最速降下曲線 をご覧下さい.
(ヒント:式(4)が使える問題です.)
3.[懸垂曲線]
密度が一様な紐を吊り下げたとき,ポテンシャルエネルギーが最小になるような紐の垂れ方(曲線)を考えて下さい.重力は一様だとします.
解答
紐の微小部分が持つ位置エネルギーを全て合わせたものを,紐全体のポテンシャルエネルギー 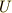 だとします.紐の微小部分
だとします.紐の微小部分 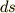 が持つ位置エネルギーは,その微小部分の高さを
が持つ位置エネルギーは,その微小部分の高さを 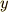 だとして
だとして 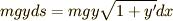 と表わされますので,
と表わされますので, 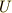 は次のように,積分で表すことができます.
は次のように,積分で表すことができます.
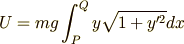
ここで 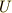 の最小値を求めたいのですから,
の最小値を求めたいのですから, 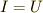 として,変分問題を解きましょう.
として,変分問題を解きましょう.
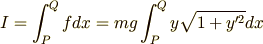
この問題では 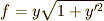 となっていて,
となっていて, 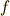 が
が  を含まない形ですから,変形オイラー方程式(4)が使える形です.解くべき式は次のようになります.
を含まない形ですから,変形オイラー方程式(4)が使える形です.解くべき式は次のようになります.
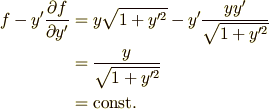
これを積分して,次の答えを得ます.
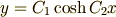
これは双曲線関数(ハイパーボリックコサイン)と呼ばれる曲線です. [*]
| [*] | 余談ですが,西洋の大きな建築物は,たいてい石で出来ています.
石を削るのはなかなか大変なことですから,自然と,予め地上で石を設計図通りに切っておいて,
上で積み上げるという方式が取られることになります.
設計図として簡単に書けるのは,定規とコンパスだけで作図できる図形ですから,
古い西洋建築に見られる曲線というのは,大方,円弧なのです.
ヨーロッパに旅行に行く機会があれば,どこの街にも古い教会などがありますから,
是非窓枠や屋根の曲線を眺めて見てください.ほとんど全て円弧の一部のはずです.
さて,たった今求めた双曲線関数ですが,これは  |
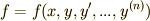
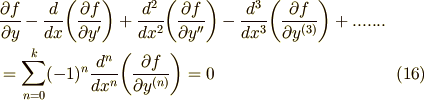
 という関数ですので,
ちょっと定規とコンパスだけで作図するのは無理そうです.
西洋で双曲線関数を始めて建築に取り入れたのは,スペインのアントニ・ガウディで,19世紀末の話です.
ところが,わが日本では,神社の屋根の微妙な反り返りなどがほとんど全て双曲線関数になっているのです!
日本では設計図を描いてから木を削るのではなく,大工さんが鎖を垂らして曲線を決めていくので,
自然と双曲線関数になってしまうのでした.こんど神社に行くようなことがあれば,是非屋根をながめて見て下さい.
西洋で,ようやくここ100年そこそこになって使われ始めた曲線が,
日本では何百年も伝統的に使われているとは,なんだか嬉しい話です.
という関数ですので,
ちょっと定規とコンパスだけで作図するのは無理そうです.
西洋で双曲線関数を始めて建築に取り入れたのは,スペインのアントニ・ガウディで,19世紀末の話です.
ところが,わが日本では,神社の屋根の微妙な反り返りなどがほとんど全て双曲線関数になっているのです!
日本では設計図を描いてから木を削るのではなく,大工さんが鎖を垂らして曲線を決めていくので,
自然と双曲線関数になってしまうのでした.こんど神社に行くようなことがあれば,是非屋根をながめて見て下さい.
西洋で,ようやくここ100年そこそこになって使われ始めた曲線が,
日本では何百年も伝統的に使われているとは,なんだか嬉しい話です.