三角関数の合成
二つの三角関数

を,一つの三角関数
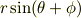
の形に変形することができます.ここで
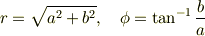
です.この関係は単振動の合成などで必要となります.
証明
三角関数の合成の関係式を,天下り的に証明します. まず,つぎの図のような直角三角形を考えます.
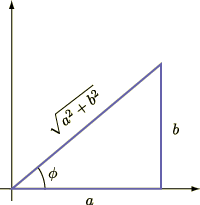
ここで 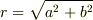 と置きます.すると図から
と置きます.すると図から
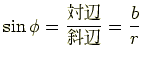
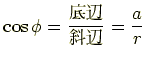
ということが分かります.つぎに 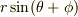 を加法定理で展開します.
を加法定理で展開します.
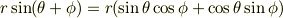
ここに先ほどの 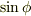 ,
, 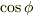 の値を代入して
の値を代入して
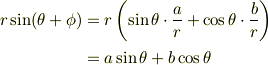
が得られ,冒頭で説明した関係式が正しいことが分かります. この関係式は,図と一緒に覚えておくと間違いがなくて良いです.
また, 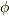 は
は
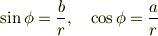
の関係を満たす角度ですから, 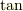 で表すと
で表すと
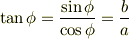
であり, 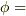 の形にするには逆三角関数にすれば良く,
の形にするには逆三角関数にすれば良く,
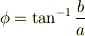
と表せます.
単振動の例
例として,二つの単振動
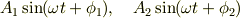
を足し合わせて一つの単振動に合成してみます. まず,合成してできあがる単振動の式を
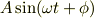
と置いておきます.この段階では 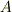 と
と 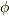 はどんな値なのか分かりません.
未知数です.合成後の式を上のように置いたのですから,
はどんな値なのか分かりません.
未知数です.合成後の式を上のように置いたのですから,
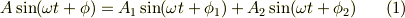
という方程式ができます.これから三角関数の合成をして,
いま未知数と置いた 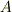 と
と 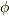 を決めます.
を決めます.
加法定理で 式(1) の右辺を展開し,整理します.
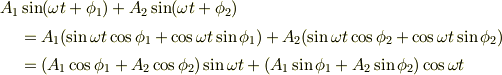
ここで,
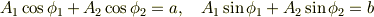
と書き換えてみますと 式(1) は
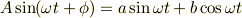
と書けます.これは三角関数の合成の式そのものですね.したがって
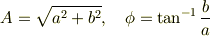
です.  と
と  を元に戻すと
を元に戻すと
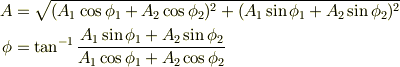
が得られます.