もう一度ベクトル3(幾何と代数の通訳)
0.幾何と代数の通訳
ベクトルは線分(大きさ,長さ)に向きという情報を加えた有向線分と考えました. ですから当然ベクトルには幾何学的な情報があります. でも和や,差,積が考えられることからわかるとおり,代数的な概念も含んでいます. 一度ベクトルを適当な [*] 座標系の成分を用いて表してあげれば,あっという間に代数的な表現が可能になるわけです.
簡単な幾何学的な条件がベクトルではどう表現できるかを見ていきましょう.
| [*] | もう一度ベクトル1,同2ではデカルト座標しか扱っていませんが実は極座標 で表しても全く問題ありません.一般的にもあまり極座標で表す事がないのは中学, 高校でもあまり扱っていないということで,極座標で考えてもあまり 『わかった!』という感には至り難いのが原因かなと思います. そういえば極座標だと,2点間の相互の座標変換も面倒です |
1.原点以外からの変位ベクトル
基本的にベクトルは「原点からどれだけ変位したか」という成分で書かれています.
でも幾何学って,図形に含まれないただの基準点なら,どんな位置にあっても関係ないはずですよね?
そこで,図形に含まれる点を始点としたベクトルではどういった書き換えを施してあげればいいのかということを覚えておく必要があります.
つまり,「点 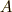 から
から 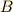 へのベクトルをどう表現すればいいか」という事がこのセクションの内容となります.
へのベクトルをどう表現すればいいか」という事がこのセクションの内容となります.
ベクトルの和のところを思い出してみましょう. 2つの表記が混在していますが点の移動を追いやすくするため,矢印表記を用いて解説しますと
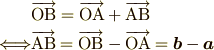
となります.この結果は覚えておきましょう.
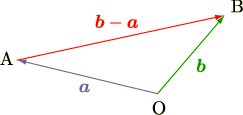
また,この結果の興味深い点は原点 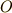 について何も条件をことわっていない点です.
つまり,原点
について何も条件をことわっていない点です.
つまり,原点 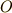 ではなくても任意の点に関して成立します.
確かに
ではなくても任意の点に関して成立します.
確かに 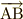 は点
は点 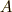 ,点
,点 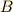 の決め方のみに依存し,原点がどの
位置にあるかは関係ないはずなので,そういった側面から眺めた条件とも合致しています.
このように数学が現実を裏切らないことが,数学が自然科学において絶大な信頼を得ている1つの理由なのかもしれません.
の決め方のみに依存し,原点がどの
位置にあるかは関係ないはずなので,そういった側面から眺めた条件とも合致しています.
このように数学が現実を裏切らないことが,数学が自然科学において絶大な信頼を得ている1つの理由なのかもしれません.
2.内分点の公式
内分点を表すベクトルの表記を天下りに書いてしまいますと
「点 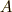 と点
と点 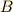 を
を 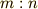 に内分する点
に内分する点  」を表す位置ベクトルは,適当な
原点(基準点)を
」を表す位置ベクトルは,適当な
原点(基準点)を  とし,
とし,
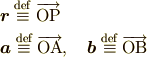
とすると
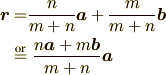
とかけます.
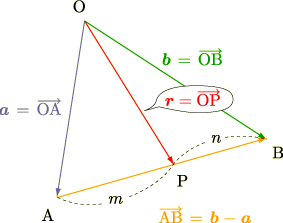
それでは証明してみましょう.いきなり上の公式が見えてしまう人は別としてやはり
"内分"しているのですから,内分している線分で考えるのが一番妥当なはずです.
以上の図の半直線  を見てください.
を見てください.
図から  が半直線
が半直線  の
の 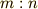 の内分点である条件としては
の内分点である条件としては
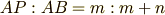
であることです.また,比は左右同じ数で割っても比には変化がないので
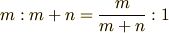
と変形します.この式は「半直線 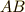 の長さを
の長さを 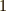 としたときに半直線
としたときに半直線  の長さは
の長さは  となる」事を言っています.この事をベクトルの表記
に反映してあげればいいのです.
となる」事を言っています.この事をベクトルの表記
に反映してあげればいいのです.
図から 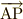 は
は 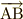 と方向が等しいので
と方向が等しいので 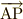 は
は 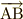 の定数倍
で表せるはずですね.ではその定数を求めなければならないのですが,その値を上記の
比で求めていたわけです.上記で求めたとおり
の定数倍
で表せるはずですね.ではその定数を求めなければならないのですが,その値を上記の
比で求めていたわけです.上記で求めたとおり
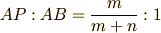
なのでベクトルな長さの関係になおすと
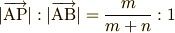
となることから

となります.大きさの比と平行な条件だけでは必ずしも係数が正とは限りませんが, 図から向き(≠方向)も等しいことから上記の式が導かれます.
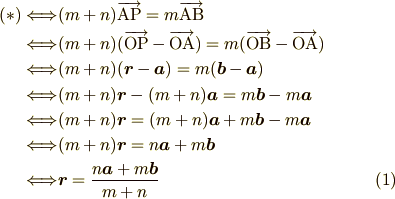
となり証明できました.特に 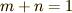 のとき
のとき 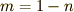 で
で

と書けます.また逆に 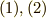 式のようにかけるときそれは直線
式のようにかけるときそれは直線 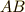 上に点
上に点 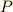 が乗っていると言い換えることが出来ます.
が乗っていると言い換えることが出来ます.
3.絶対値の公式
先ずこの公式を天下り的に紹介しますと
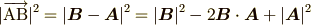
となります.二項展開に非常に似ているので覚えるのもそれほど苦にはならないかと 思います.この公式の利用例を紹介しておきます. 証明は余弦定理を用いて行います.簡単なので余力があれば実行してみましょう
どうしても  から
から  の距離を測りたいときに
の距離を測りたいときに  と
と  ,
, 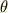 しかわかっていないことがあります. [†]
しかわかっていないことがあります. [†]
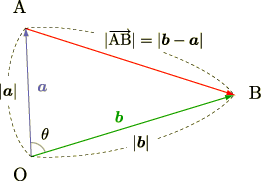
もし具体的に 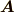 と
と 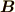 がわかれば内積を計算するなどして上記の
3量は求まることを確認してみてください.このときに
がわかれば内積を計算するなどして上記の
3量は求まることを確認してみてください.このときに 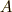 から
から 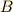 の距離を上記の
3量で表す公式があります.方程式として変形したいので答えが求まったフリを
して
の距離を上記の
3量で表す公式があります.方程式として変形したいので答えが求まったフリを
して 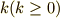 などと置いておきます.
などと置いておきます.
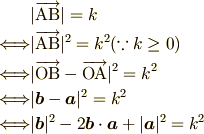
4行目から5行目の変形が該当する公式です.以上の左辺は計算できるので左辺の値の 平方根をとれば具体的に値が求まります.
| [†] | 中学校で習う三角形の三つの合同条件を覚えているでしょうか?その中の二辺夾角相等(二辺と
その間の角がそれぞれ等しい)がまさにこの内容です.つまり, 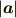 と と  とその間
の角を定めれば三角形は一意に定まるということです.確かに二本のペンの根っこをくっつけ
間の角度をグリグリ動かしてやれば間の角度1つにつき三角形が定まることは感覚的に納得できる
と思います. とその間
の角を定めれば三角形は一意に定まるということです.確かに二本のペンの根っこをくっつけ
間の角度をグリグリ動かしてやれば間の角度1つにつき三角形が定まることは感覚的に納得できる
と思います. |
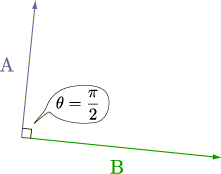
4.直交条件
2つのベクトルが直交する条件ってどう表せるのか?というのがこのセクションの テーマです.
2つのベクトルの関係を表す指数として内積がありました.
2つのベクトル 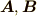 の内積はそれぞれ大きさ
の内積はそれぞれ大きさ 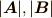 となす角
となす角 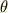 を用いて
を用いて
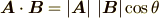
と表せました.
「2つのベクトルが直交する」ということは「2つのベクトルのなす角が 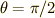 .」ということなので
.」ということなので 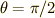 という条件をを入れてあげれば良いのではないでしょうか.
という条件をを入れてあげれば良いのではないでしょうか.
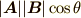 に上記の条件を代入すると
に上記の条件を代入すると 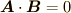 となるので,"直交する"と言う条件は
となるので,"直交する"と言う条件は
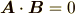
という条件を考えればいい事になります. 代数的な側面においては内積を具体的に成分で書き下して

という条件で考えます. [‡]
蛇足:直交条件を外積で表すと…
ベクトルの外積 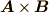 にも角度の部分があるので外積で作られるベクトルの大きさ
にも角度の部分があるので外積で作られるベクトルの大きさ 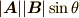 に
に 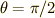 を
代入すると
を
代入すると 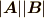 という結果が得られますが,
という結果が得られますが,
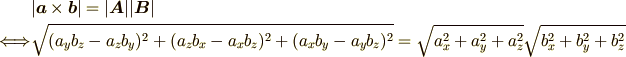
となるだけで変数が左右にばらばらに散らばっちゃって使い物になりません.
因みにこれを両辺平方して 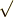 を外すして整理すると
を外すして整理すると
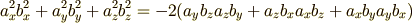
となりますが,これを移項したものは内積の直交条件で導いた式を2乗すると得られます. かなり計算した割には結局ほぼ同じ式を計算していたわけです.(まぁ数学的には同値になってもらわないと困るので当たり前っちゃあ当たり前ですが…)
内積を計算した方が 楽… ですね.
| [‡] | 「直角だから内積が0」というのは純粋な数学的には誤りです. 空間に浮かぶ幾何学的なもの(矢印を含みます)を天下り的に認め,「直角に交わる」ということも「なす角が90度である」という事実を前提無しに受け入れるならこの議論で構いませんが,数学的には不十分な議論です. 数学的には「空間」という言葉は抽象化されていて,日常用語の意味とは必ずしも一致しません. 数学的には「ベクトル空間である」→「内積が定義できる(内積空間である)」→「角度という概念が導入できる」という流れになります. ここで議論している空間は基本的に3次元ユークリッド空間に限定していますから,日常用語における空間とほぼ同じです. 数学で扱うような一般の空間とは違うということと,議論の順番が多少前後していることに少し注意しておいてください. |
5.付録:ベクトルの外積の直交性とその大きさの確認
もう一度ベクトル2では外積ベクトルを天下り的に「こうなります」としてしまったので 直交性を確認したついでにその大きさが2ベクトルにより作られる平行四辺形になって いるか確認してしまいましょう
外積で作られるベクトルはもとの2つベクトルに直交しているか?
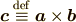
とすると「 もう一度ベクトル2 」から  は
は  と
と 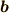 の各成分を
使って
の各成分を
使って
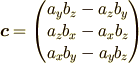
と書けます.ここで,  と
と  の内積をとります.
内積は各成分ごとの和を取ればよかったので
の内積をとります.
内積は各成分ごとの和を取ればよかったので
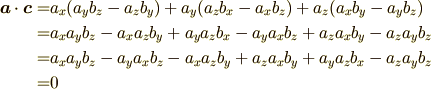
となりました.内積が 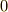 なので直交することになります.
当然
なので直交することになります.
当然 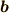 に対しても全く同様の計算を行うことにより,内積が
に対しても全く同様の計算を行うことにより,内積が 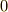 になることを
確認できます.
になることを
確認できます.
実はここで, 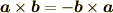 に注意すると
に注意すると
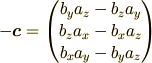
となり,直交性を示したいだけならばその向き(≠方向)には興味がないはずなので  がついて逆を向いていても問題はないはずですね!?つまり
がついて逆を向いていても問題はないはずですね!?つまり

ということです
そこで 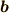 と"
と" 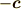 "の内積を考えます.その成分にによ〜く注意して
みると
"の内積を考えます.その成分にによ〜く注意して
みると  と
と  の内積のそれと対応が全く一致しています.
の内積のそれと対応が全く一致しています.
したがって全く同じ計算により内積が 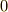 になることが言えるのでで直交している
ことがいえます. [§]
になることが言えるのでで直交している
ことがいえます. [§]
| [§] | 「何をまどろっこしいことを」と思った方もいると思います.確かにこんな簡単な計算なら 代入して計算をしたほうが早いのですが,数学の定理を証明する際に計算が多量になる ことが目に見えたりしている場合別の定理を利用したりこのようにトリッキーに証明 したりします.正直なところ,人に聞くと「ズルイ」と思いますが,自分で思いつくと 数学者の仲間入りをした気になってしまいます.(あくまでも思い違いですが…) |
外積で作られるベクトルの大きさははもとの2つのベクトルが張る平行四辺形の面積に等しいか?
「 もう一度ベクトル2 」では 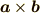 の
大きさは
の
大きさは 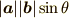 と定義しました.これを確認するために二通り
に表してその値が一致することを見てみましょう.
と定義しました.これを確認するために二通り
に表してその値が一致することを見てみましょう.
このベクトルの大きさの中で 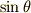 という量に注目します.
三角関数には
という量に注目します.
三角関数には 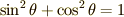 という恒等式があったのでそれを利用
して
という恒等式があったのでそれを利用
して 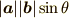 を書き換えると
を書き換えると
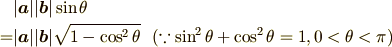
ここで内積の図形的な定義である 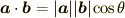 を
を 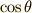 についてといて代入すると
についてといて代入すると
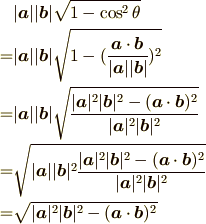
とかなりコンパクトになったのでここに具体的な成分を代入していきます. [¶]
まず 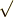 の中身をばらすと
の中身をばらすと
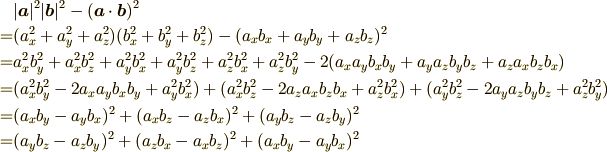
となりました.一方 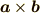 のほうは
のほうは
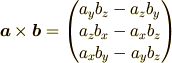
と表せるのでその大きさは

と成分を用いてかけるはずですがこれは先ほどの計算の  の中身と一致
しています.つまりベクトルの大きさは
の中身と一致
しています.つまりベクトルの大きさは 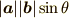 と
等しいことがわかりました.
と
等しいことがわかりました.
| [¶] | この値を 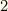 で割ったものは二つのベクトルで作られる三角形の面積になっている
事から受験生などは覚えておくと便利です.正四面体の体積への応用なんかも楽チン
かもしれません で割ったものは二つのベクトルで作られる三角形の面積になっている
事から受験生などは覚えておくと便利です.正四面体の体積への応用なんかも楽チン
かもしれません |
6.まとめ
以上で求めたベクトルの式を眺めてみるとほとんどのものが,幾何学的な条件を反映させた式を少し変形したものばかりです.でも,そのベクトルをひとたび, 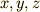 を用いて表せば,デカルト座標系の条件式が手に入るわけです.純粋な数学の証明でも,初等幾何学の定理だけで攻めるか,座標を設定して攻めるかという選択肢に「ベクトルで攻める」という選択肢が1つ加わったわけです.
を用いて表せば,デカルト座標系の条件式が手に入るわけです.純粋な数学の証明でも,初等幾何学の定理だけで攻めるか,座標を設定して攻めるかという選択肢に「ベクトルで攻める」という選択肢が1つ加わったわけです.
物理的には,重心の位置ベクトルが内分点を表すベクトルで表現できたり,内積が0という条件から,変位ベクトルと力のベクトルが直交しているのでその力の成す仕事は0などと考えることができるわけです. 以下に,このセクションの公式とその使い方・特徴を簡単にまとめておきます
- 点
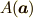 から点
から点 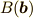 へ向かうベクトル
へ向かうベクトル 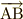
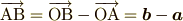
非常に基本的な公式です.和や差と同じくらい頻繁に出てきます.
- 点
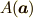 と点
と点 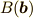 を
を 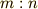 に内分するベクトル
に内分するベクトル
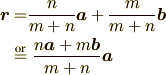
高校なんかの定期テストや,私大入試の小問なんかでよくでます. 「与えられた式を変形して適当な置換を行うとこの形になるから点の存在条件がわかる」という出題もあり.物体の重心の位置の座標も内分点で表せます.
- 絶対値の公式
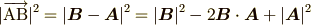
2つのベクトルの相互関係を求めたり,内積を積極的にとることにより,三角形の形状決定等が出来る.
- 2つのベクトルの直交条件

文字通り直交条件に用いることが大半.右辺が 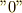 というかなり特殊な値になるため,計算はあまり煩雑にはならない.力と変位が直交しているという条件や,平面の法線を定量的に求めるときにも出てきます.
というかなり特殊な値になるため,計算はあまり煩雑にはならない.力と変位が直交しているという条件や,平面の法線を定量的に求めるときにも出てきます.