行列の積の表現方法

行列をベクトルの集合と見た時の積の表現方法について書きます． 短い記事です．

その一（内積の集合）

まずは一つ目，おそらく，これは皆さんよくご存じだと思います． ３次の正方行列A,Bを，Aは行ベクトルの集合，Bは列ベクトルの集合と考えます． すると，普通のベクトルを列ベクトルとして，行ベクトルをその転置( ^T )として，

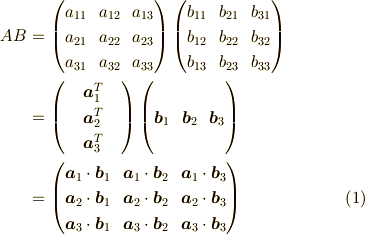
AB &=\begin{pmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{pmatrix}\begin{pmatrix}b_{11} & b_{21} & b_{31} \\b_{12} & b_{22} & b_{32} \\b_{13} & b_{23} & b_{33}\end{pmatrix} \\&=\begin{pmatrix}\ & \bm{a}_1^T & \ \\\ & \bm{a}_2^T & \ \\\ & \bm{a}_3^T & \ \end{pmatrix}\begin{pmatrix} \ & \ & \ \\\bm{b}_1 & \bm{b}_2 & \bm{b}_3 \\ \ & \ & \ \end{pmatrix} \\&=\begin{pmatrix}\bm{a}_1 \cdot \bm{b}_1 & \bm{a}_1 \cdot \bm{b}_2 & \bm{a}_1 \cdot \bm{b}_3 \\\bm{a}_2 \cdot \bm{b}_1 & \bm{a}_2 \cdot \bm{b}_2 & \bm{a}_2 \cdot \bm{b}_3 \\\bm{a}_3 \cdot \bm{b}_1 & \bm{a}_3 \cdot \bm{b}_2 & \bm{a}_3 \cdot \bm{b}_3\end{pmatrix} \tag{1}

と，このように各成分がベクトルの内積になります．

その二（ダイアドの集合）

次は，３次の正方行列A,Bを，Aは列ベクトルの集合，Bは行ベクトルの集合と考えます． すると，

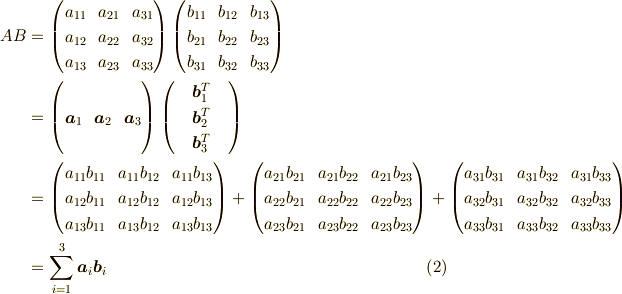
AB &=\begin{pmatrix}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33}\end{pmatrix}\begin{pmatrix}b_{11} & b_{12} & b_{13} \\b_{21} & b_{22} & b_{23} \\b_{31} & b_{32} & b_{33}\end{pmatrix} \\&=\begin{pmatrix} \ & \ & \ \\\bm{a}_1 & \bm{a}_2 & \bm{a}_3 \\ \ & \ & \ \end{pmatrix}\begin{pmatrix}\ & \bm{b}_1^T & \ \\\ & \bm{b}_2^T & \ \\\ & \bm{b}_3^T & \ \end{pmatrix} \\&=\begin{pmatrix}a_{11}b_{11} & a_{11}b_{12} & a_{11}b_{13} \\a_{12}b_{11} & a_{12}b_{12} & a_{12}b_{13} \\a_{13}b_{11} & a_{13}b_{12} & a_{13}b_{13} \end{pmatrix}+\begin{pmatrix}a_{21}b_{21} & a_{21}b_{22} & a_{21}b_{23} \\a_{22}b_{21} & a_{22}b_{22} & a_{22}b_{23} \\a_{23}b_{21} & a_{23}b_{22} & a_{23}b_{23} \end{pmatrix}+\begin{pmatrix}a_{31}b_{31} & a_{31}b_{32} & a_{31}b_{33} \\a_{32}b_{31} & a_{32}b_{32} & a_{32}b_{33} \\a_{33}b_{31} & a_{33}b_{32} & a_{33}b_{33} \end{pmatrix} \\&=\sum_{i=1}^3 \bm{a}_{i} \bm{b}_{i} \tag{2}

となります．最後の表現は少し説明がいるかもしれません．

これはダイアド（ダイアド積，ダイアディックともいう） と言うもので，

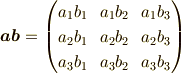
\bm{a} \bm{b}=\begin{pmatrix}a_{1}b_{1} & a_{1}b_{2} & a_{1}b_{3} \\a_{2}b_{1} & a_{2}b_{2} & a_{2}b_{3} \\a_{3}b_{1} & a_{3}b_{2} & a_{3}b_{3} \end{pmatrix}

で定義されます．ベクトルを 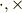\cdot , \times 等を使わずにただ並べる積です． 関連記事として， 続ベクトルの回転 ， 正方行列の三連続積の展開 を挙げておきます． よかったら，そちらもご覧ください．

その３（列ベクトルの線形結合）

話はまだ続きます．では，A,Bともに列ベクトルだと見たらどうなるでしょうか？ それは，

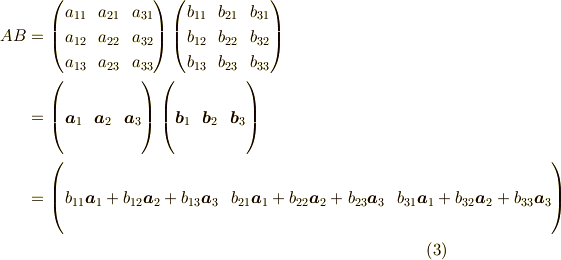
AB &=\begin{pmatrix}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33} \end{pmatrix}\begin{pmatrix}b_{11} & b_{21} & b_{31} \\b_{12} & b_{22} & b_{32} \\b_{13} & b_{23} & b_{33}\end{pmatrix} \\&=\begin{pmatrix} \ & \ & \ \\\bm{a}_1 & \bm{a}_2 & \bm{a}_3 \\ \ & \ & \ \end{pmatrix}\begin{pmatrix} \ & \ & \ \\\bm{b}_1 & \bm{b}_2 & \bm{b}_3 \\ \ & \ & \ \end{pmatrix} \\&=\begin{pmatrix} \ & \ & \ \\b_{11}\bm{a}_1 + b_{12}\bm{a}_2 + b_{13} \bm{a}_3 & b_{21}\bm{a}_1 + b_{22}\bm{a}_2 + b_{23} \bm{a}_3 & b_{31}\bm{a}_1 + b_{32}\bm{a}_2 + b_{33} \bm{a}_3 \\ \ & \ & \ \end{pmatrix}\tag{3}

とこの様になります．二つとも行ベクトルとして見たときについては， ご自分で計算してみてください． 今度は，Bの行ベクトルの線形結合が積の行列ABの行ベクトルとなります． それでは，今日はこの辺で．お疲れ様でした．