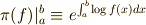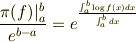新たな積分の形式
小ネタです.あらたな積分の形式を考えてみました. でも残念なことに,応用には向かなさそうです.
復習(高校でならう積分)
高校でならう積分の復習をしてみます. リーマン積分ってやつですね. ちょっとおおざっぱですが,お許しください.
関数f(x)のaからbまでの定積分を定義するには,
まず区間 ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) をn等分してできる,n+1個の分割点に
をn等分してできる,n+1個の分割点に
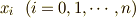 と名前をつけます. [*]
そして,その間隔を
と名前をつけます. [*]
そして,その間隔を 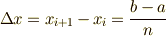 とします.
とします.
| [*] | 具体的な書くと 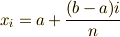 です. です. |
そこで,定積分を以下のように定義するのでした.
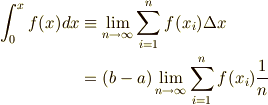
ここで, 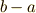 を前に出したのは,今後の布石です.
最後の行をよく見てみると,(b-a)×(n個の点でのf(x)の値の平均)になっていますよね.
つまり,すべての点の平均値に区間の長さをかければ,曲線の下の面積になるわけです.
を前に出したのは,今後の布石です.
最後の行をよく見てみると,(b-a)×(n個の点でのf(x)の値の平均)になっていますよね.
つまり,すべての点の平均値に区間の長さをかければ,曲線の下の面積になるわけです.
新たな積分
ここで,今回のメインコンテンツは, さっき出てきた平均を,相加平均じゃなくて相乗平均にしてしまおうというのが, 基本のアイディアです.では,さっそく変えてみましょう.
簡単のため,区間 ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) ではなく,区間
ではなく,区間 ![[0,1]](./ccfcd347d0bf65dc77afe01a3306a96b.png) にしておきます.
汎関数の一種なので,
にしておきます.
汎関数の一種なので, 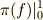 とでも,表現しましょうか.
とでも,表現しましょうか.
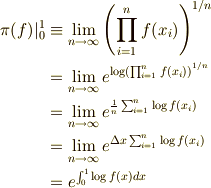
なんだ,結局既存の計算手法で表現できるものでしたね.
拡張するには,出てきた定積分の区間を ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) とするのが,自然だと思います.
以下に,一般の形を書きます.
とするのが,自然だと思います.
以下に,一般の形を書きます.
積分の他の拡張
平均を調和平均にした場合,詳しくは書きませんが同様に,
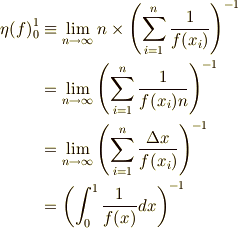
同様に区間を一般化して,
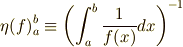
となります.
これは,例えば無限に細い単位長さあたりの抵抗の異なる抵抗を束ねた時, 全体の抵抗はどうなるか計算できます.
最後に幾何平均と調和平均が定義できるためには,区間[a,b]に於いて,f(x)>0が必要であることを付け加えておきます.
それでは,今日はこの辺で. ごきげんよう(^o^)/~
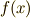 の区間
の区間