1/x周辺の積分(log x の近傍で)
さて, 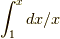 はなんでしょう?そうです,
はなんでしょう?そうです, 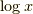 ですね.
今回は,αを-1に近づけたときの
ですね.
今回は,αを-1に近づけたときの 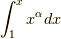 の挙動を調べてみます.
の挙動を調べてみます.
動機
べき関数の積分に於いて,
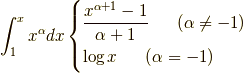
ですが, 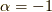 の時だけ別種の関数に見えています.
では,
の時だけ別種の関数に見えています.
では,  を
を 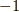 とは異なる,しかし,ごく近い実数にしたら,
とは異なる,しかし,ごく近い実数にしたら, 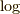 に収束するのか,
調べました.
に収束するのか,
調べました.
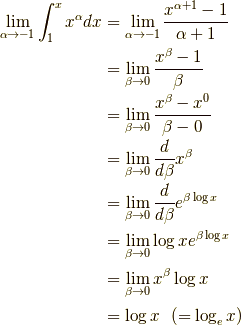
この様に確かに, 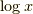 に収束しました.
実は幾何学的な解釈をすれば,
積分は曲線の下の面積なので,曲線が連続的に移り変わるなら,
おかしなことは起こるはずがなかったのです.
に収束しました.
実は幾何学的な解釈をすれば,
積分は曲線の下の面積なので,曲線が連続的に移り変わるなら,
おかしなことは起こるはずがなかったのです.
発散と収束の境界:log x
もう少し考えてみましょう.
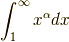
は, 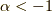 で収束,
で収束, 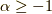 で発散したのでした.
で発散したのでした.
横軸が対数の片対数のプロットでその様子を見てみましょう.それが,下の図です.
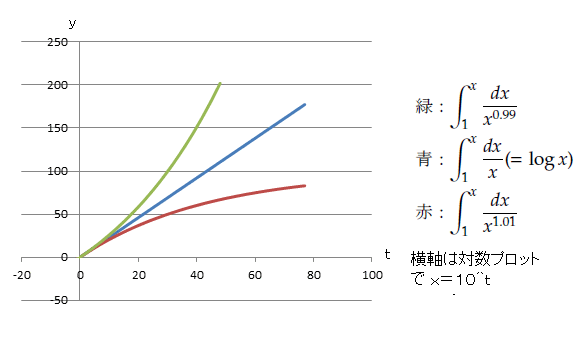
見ると, 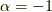 の直線を境に上に凸な
の直線を境に上に凸な 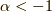 と下に凸な
と下に凸な 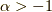 で
きれいに分かれることが分かります.ちなみに赤線は
で
きれいに分かれることが分かります.ちなみに赤線は
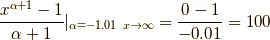
に収束します. それでは今日はこの辺で,お疲れ様でした.