長さ一定の棒と一次関数の極値(ラグランジュの未定乗数法)
この記事は,Joh氏の ラグランジェの未定乗数法 の(蛇足的)例題です. ちなみに,ラグランジュなのかラグランジェなのか疑問に思うかもしれませんが, この人はフランス人で,Lagrangeと書き,フランス語読みがラグランジュ, 英語読みがラグランジェです.
問題
定数 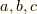 がある.独立変数
がある.独立変数 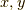 が,
が,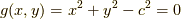 を満たしながら
変化する時,
を満たしながら
変化する時, 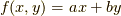 の最大・最小値を求めよ.
の最大・最小値を求めよ.
ラグランジュの未定乗数法
ここでラグランジュの未定乗数法という手法を用います.
未定乗数を 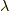 として,
として,
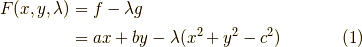
とおくと,極値の条件は,
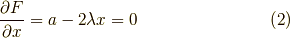
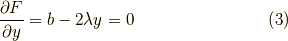
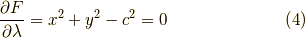
から求まります.
まず, 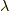 を求めます.
式
を求めます.
式 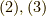 を
を 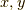 について解いて,式
について解いて,式 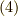 に代入すると,
に代入すると,
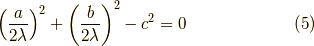
ここで 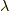 について解くと,
について解くと,

ここで, 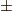 の二解の内,最大値を表す
の二解の内,最大値を表す 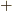 の方について考えていきます.
もちろん,これだけから最大値・最小値・停留値を区別することはできません.
私は結果を知っているので,言っているだけです.
すると,式
の方について考えていきます.
もちろん,これだけから最大値・最小値・停留値を区別することはできません.
私は結果を知っているので,言っているだけです.
すると,式 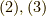 より,
より, 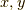 が求まり,
が求まり,
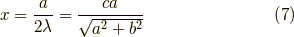
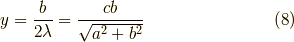
となります.
よって最大値 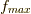 は,
は, 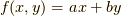 にこの
にこの 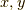 を代入したときなので,
を代入したときなので,
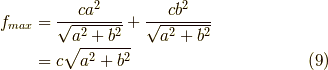
となり最大となります.
蛇足
僕はいつも気になるのですが,
平面 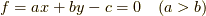 に対して,
偏微分係数,もしくは,ナブラ
に対して,
偏微分係数,もしくは,ナブラ  を用いた勾配,
を用いた勾配,
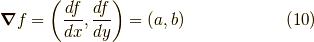
の時,もっともきつい勾配の方向は,  軸かな?と思ってしまいます.
しかし,それは単位距離
軸かな?と思ってしまいます.
しかし,それは単位距離 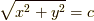 だけ進んだ時の増加量を比較するべき
なので,
だけ進んだ時の増加量を比較するべき
なので, 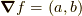 の方向がもっともきつい傾斜なんですね.
スキー場等で実感しましょう(笑).なお,この辺の話は,
やかん氏の ベクトル解析奮闘記1 も参考になると思います.
それでは,今日はこの辺で.お疲れ様でした.
の方向がもっともきつい傾斜なんですね.
スキー場等で実感しましょう(笑).なお,この辺の話は,
やかん氏の ベクトル解析奮闘記1 も参考になると思います.
それでは,今日はこの辺で.お疲れ様でした.