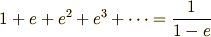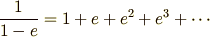無限等比級数の和
初項 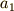 ,公比
,公比  の等比数列
の等比数列 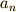 において,
において, 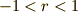 のとき
のとき
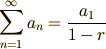
という公式が成り立ちます.等比数列をずっとずっと足しあわせていったら, 上の式の右辺になるというのです. 無限に足しあわせたのに一定の値になる(収束する)というのはちょっとフシギな感じがします.
導きかた
この公式を導くのは簡単です.等比数列の和の公式

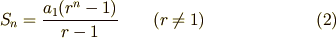
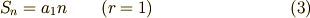
を思い出します.式(2)において, 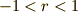 のときは
のときは
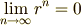
が言いえます.たとえば 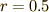 の場合,
の場合,
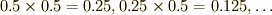 と,
掛け続けるといつかはゼロになりそうです.
上の式は,絶対値が 1 より小さい数を永遠に掛け続けて行くと,
いつかゼロになるということです.そうすると式(2)は
と,
掛け続けるといつかはゼロになりそうです.
上の式は,絶対値が 1 より小さい数を永遠に掛け続けて行くと,
いつかゼロになるということです.そうすると式(2)は
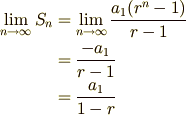
となります.無限等比級数の和が収束するのは,
足しあわせる数の値がだんだん小さくなって,いつかはゼロになるからです.
もちろん, 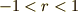 のとき,という条件つきですが.
のとき,という条件つきですが.
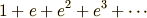
 の等比級数です.もしも
の等比級数です.もしも 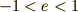 ならば
ならば