ガウス関数のモーメントを簡単に計算する方法
この記事では,確率・統計で使われる,ガウス分布のモーメント計算を簡単にする為のテクニックを紹介します.
ちなみに,
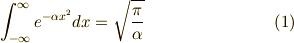
は,既知であるとします.ご存知のない方は,COさんの, ガウス積分の公式 をご覧ください.
モーメントとガウス分布
分布関数 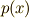 に対し,
に対し, 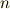 次(
次( 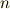 は整数)のモーメント
は整数)のモーメント  とは,
とは,
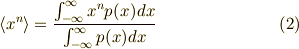
で定義されます.ここで,式 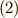 の分母は正規化を表しており,
の分母は正規化を表しており,
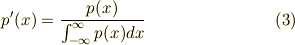
とすれば,分布関数 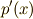 は総和が
は総和が 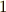 に等しいので,
変数
に等しいので,
変数  での値を取る時の確率が
での値を取る時の確率が 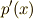 となっています.
となっています.
ところで,ガウス分布とは実数 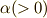 として,
として,
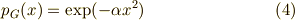
という釣鐘(つりがね)型の分布関数をした分布です.この関数のことをガウス関数,または,ガウシアンと呼びます. グラフにすると
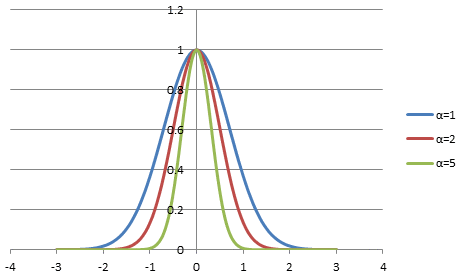
と,このようになります.パラメータの 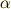 は,大きいほど原点に局在する鋭い分布関数になります.
は,大きいほど原点に局在する鋭い分布関数になります.
ガウス関数のモーメント
ここで,ガウス分布に関するモーメントを考えてみましょう.モーメントを表す括弧に 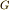 の添え字をつけて,
ガウス分布であることを表示しておきます.
の添え字をつけて,
ガウス分布であることを表示しておきます.
ちなみに,
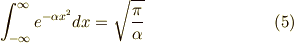
は,既知であるとします.
すると,まず 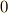 次のモーメントは,
次のモーメントは,
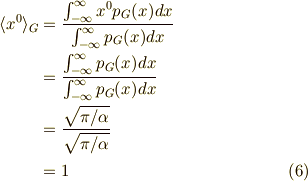
となります.これは簡単でしたね.
次は, 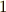 次のモーメントです.
次のモーメントです.

は,
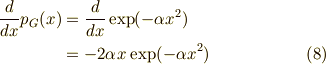
ですから,
![\int_{-\infty}^\infty x \exp(- \alpha x^2) dx &= \frac{1}{-2 \alpha }\left[ \exp(- \alpha x^2) \right]_{-\infty}^\infty \\&= 0-0 = 0 \tag{9}](./ca676ce2ae91fddecb6fd3eb7f9efeb9.png)
より,

です.一般にガウス関数の奇数次のモーメントは奇関数の積分範囲が原点対称な積分ですから,
ゼロとなります.もし,どうしても計算で示したいときは,  と置換積分を行うとよいでしょう.
と置換積分を行うとよいでしょう.
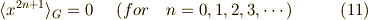
それでは, 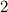 次のモーメントを求めます.
それは部分積分を利用します.
次のモーメントを求めます.
それは部分積分を利用します.
![\int_{-\infty}^\infty x^2 \exp(- \alpha x^2) dx &= \dfrac{1}{-2 \alpha} \int_{-\infty}^\infty x \dfrac{d}{dx}\left( \exp(- \alpha x^2) \right) dx \\&= \frac{-1}{2 \alpha }\left[ x \exp(- \alpha x^2) \right]_{-\infty}^\infty + \dfrac{1}{2 \alpha} \int_{-\infty}^\infty \dfrac{d}{dx}\left( x \right) \exp(- \alpha x^2) dx \\&= 0 + \dfrac{1}{2 \alpha} \int_{-\infty}^\infty \exp(- \alpha x^2) dx \\&= \dfrac{1}{2 \alpha}\sqrt{\dfrac{\pi}{\alpha}} \tag{12}](./0be205072892186abac4d1a3b4070b9e.png)
よって, 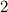 次のモーメントは,
次のモーメントは,
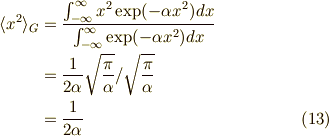
非負の整数 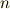 に対して,
に対して,  は部分積分を繰り返すことで,
求めることができます.
は部分積分を繰り返すことで,
求めることができます.
そんな面倒をしなくても
と,ここまでモーメントの計算をしてきましたが, 実は簡単に済ませる方法があるのです.それには,
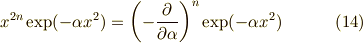
と書けることを利用します.  での積分と
での積分と 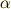 での積分を入れ替えます.
つまり,
での積分を入れ替えます.
つまり,
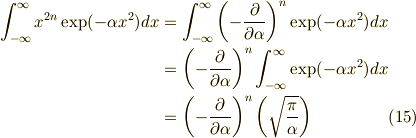
よって,
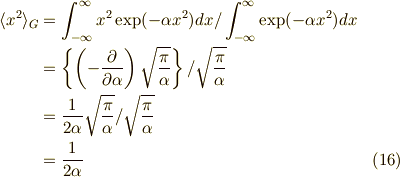
となり,

となり,一般に,
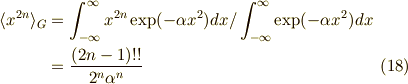
となることが分かります. ただし,

です.それでは,今日はこの辺で.お疲れ様でした.