オイラーの公式
さりげなく多用されているオイラーの公式は,複素数と実数の橋渡しとしてかなり重要です. オイラーの公式はつぎの形をしています.
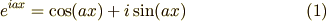
ここで, 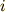 は虚数単位,
は虚数単位,  は定数,
は定数,  は変数です.
この公式は知らないととても困る上に恥ずかしいので,憶えておかなければなりません.
は変数です.
この公式は知らないととても困る上に恥ずかしいので,憶えておかなければなりません.
導いてみる
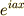 をべき級数展開するとつぎのようになります.
をべき級数展開するとつぎのようになります.
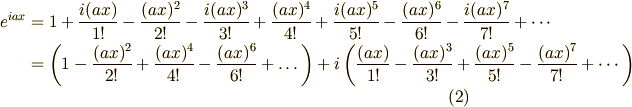
とりあえず 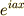 はこういうふうに展開できるのだと思っておいてください.
虚数単位
はこういうふうに展開できるのだと思っておいてください.
虚数単位 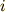 が入っているので,
が入っているので, 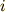 で括っています.
で括っています.
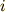 でくくった方が虚数部分,もう一方が実数部分です.
でくくった方が虚数部分,もう一方が実数部分です.
式(2) と 式(1) のオイラーの公式を比べて見ると,実数部分が 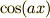 で,
虚数部分が
で,
虚数部分が 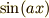 なんでしょ,という気持ちになってきます.
その通りで
なんでしょ,という気持ちになってきます.
その通りで 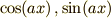 のべき級数はそれぞれつぎのようになります.
のべき級数はそれぞれつぎのようになります.
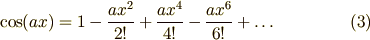
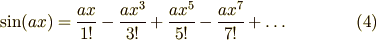
式(3) と 式(4) を 式(2) に代入すると,オイラーの公式
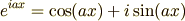
が得られます.なんだかだまされたような感じですが,とりあえずオイラーの公式は導けました.
使いみち
「  の肩に虚数単位
の肩に虚数単位 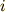 が乗っていたら,
が乗っていたら, 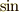 と
と 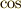 で表現できる」
ということを肝に命じておきましょう.
で表現できる」
ということを肝に命じておきましょう. 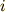 に負号がついて
に負号がついて 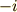 になったときは,
になったときは,
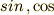 で表したときの
で表したときの 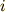 の符号が変わるだけです.
の符号が変わるだけです.
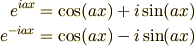
また,上の2つの式を足し合わせると普通の 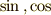 を
を
 を使って表すことができます.
を使って表すことができます.
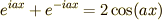 より
より 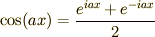
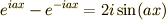 より
より 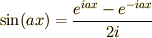
この関係も活躍するので憶えておくといいですね.