包絡線
関数が何かパラメータを含んでいるとき,パラメータを変化させれば関数の形も変わっていきます.そのとき,これらの関数に全て接するような曲線を包絡線と呼びます.例えば,  という関数で,パラメータ
という関数で,パラメータ  を次々と変化させていくと,次の図に描いてあるように半径
を次々と変化させていくと,次の図に描いてあるように半径 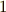 の円が中心を曲線
の円が中心を曲線 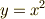 上に置きながら動いていくことになります.
上に置きながら動いていくことになります.

このときの包絡線は,図で赤く示した二本の曲線になります.全ての円がこの赤い曲線に接しているというのが分かると思います.
陰関数の包絡線
陰関数というのは 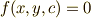 のように左辺が関数,右辺が
のように左辺が関数,右辺が 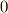 の形の関数のことでした.(
の形の関数のことでした.( 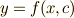 のように,『ある変数=右辺』の形になっているものを陽関数と言うのでした.)
のように,『ある変数=右辺』の形になっているものを陽関数と言うのでした.)
陰関数 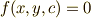 の包絡線は,次の連立方程式を解いて
の包絡線は,次の連立方程式を解いて  を消去することで与えられます. [*]
を消去することで与えられます. [*]


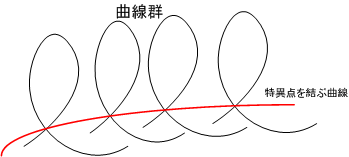
| [*] | 式(1)は曲線群 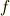 に接するということ,式(2)は曲線群 に接するということ,式(2)は曲線群 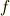 上の点であるという意味ですから,式(1)(2)を連立して得られる曲線が,曲線群 上の点であるという意味ですから,式(1)(2)を連立して得られる曲線が,曲線群  の包絡線になっているというのは明らかだと思います.ただし,やや上級レベルの話になりますが,曲線に特異点がある場合,曲線群の特異点を結ぶ曲線もやはり式(1)(2)によって表されることに注意しなければなりません.意味します.つまり上の包絡線の式は必要条件にすぎないのです.本稿では特異点を持つ曲線群は考えませんが,読者のみなさんが一般の曲線群に対して包絡線を考える場合には注意する必要があります. の包絡線になっているというのは明らかだと思います.ただし,やや上級レベルの話になりますが,曲線に特異点がある場合,曲線群の特異点を結ぶ曲線もやはり式(1)(2)によって表されることに注意しなければなりません.意味します.つまり上の包絡線の式は必要条件にすぎないのです.本稿では特異点を持つ曲線群は考えませんが,読者のみなさんが一般の曲線群に対して包絡線を考える場合には注意する必要があります. |
例
長さ  の線分が,
の線分が,  軸と
軸と  軸に接しながら滑るように動く場合を考えます.このときの包絡線はどうなるでしょう?
軸に接しながら滑るように動く場合を考えます.このときの包絡線はどうなるでしょう?
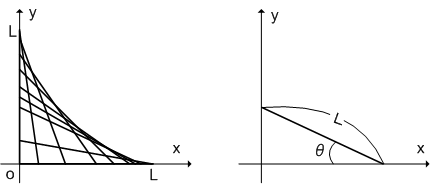
線分が次々と滑って行くと,上左図のようになることが想像できるでしょうか.一本一本の線分は上右図のようになっています.図の直線の方程式は 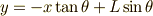 と書けますので,少し変形すれば,線分の方程式は
と書けますので,少し変形すれば,線分の方程式は 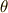 をパラメータとして次のように書くことが出来ます.
をパラメータとして次のように書くことが出来ます.
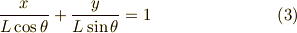
式(3)の両辺に 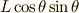 を掛けて,次のように陰関数の形にまとめましょう. これで公式が使える形になりました.
を掛けて,次のように陰関数の形にまとめましょう. これで公式が使える形になりました.
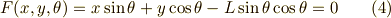
これを 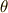 で偏微分すると次のようになります.
で偏微分すると次のようになります.

式(4)と式(5)を連立して 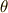 を消去します.
を消去します.
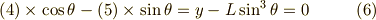
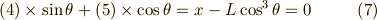
式(6)(7)より,  ,
, 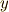 が次のように求められました.
が次のように求められました.

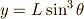
この  ,
, 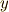 に対して,
に対して, 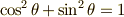 の関係を利用して
の関係を利用して 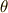 を消去すると次の式が得られます.これが包絡線の方程式になります.かなりきれいな形にまとまりました.
を消去すると次の式が得られます.これが包絡線の方程式になります.かなりきれいな形にまとまりました.

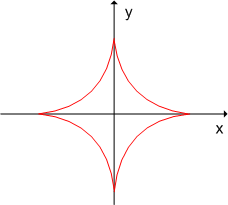
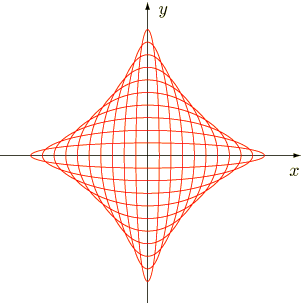
これは星芒形(アステロイドとも呼ぶ)と呼ばれる次のような図形です.
関数がパラメータ表示になっている場合の包絡線
関数が 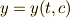 ,
, 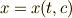 のようにパラメータ表示されている場合,包絡線は次の式で表されます. [†]
のようにパラメータ表示されている場合,包絡線は次の式で表されます. [†]

| [†] | 曲線 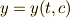 , , 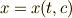 とその包絡線を考えます.包絡線に接している,ある点における曲線傾きは, とその包絡線を考えます.包絡線に接している,ある点における曲線傾きは,  平面上で 平面上で  と与えられるでしょう.一方,パラメーター と与えられるでしょう.一方,パラメーター  が少し変化したとき,この点は が少し変化したとき,この点は  方向に 方向に 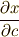 , , 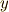 方向に 方向に 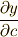 だけ変化するはずなので,傾き だけ変化するはずなので,傾き  の曲線に沿って変化することになります.もしも の曲線に沿って変化することになります.もしも 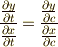 が成り立てば,この点は が成り立てば,この点は  が変化するとき,接線にそって動いて行くことになります.この点の軌跡は包絡線に他なりません.この条件を少し見やすくまとめたのが上の公式です.ただし,陰関数のセクションで註に書いたことと同じですが,この公式は曲線に特異点がある場合には包絡線以外の曲線をも含みます.また,包絡線の存在そのものを保障するものでもありません. が変化するとき,接線にそって動いて行くことになります.この点の軌跡は包絡線に他なりません.この条件を少し見やすくまとめたのが上の公式です.ただし,陰関数のセクションで註に書いたことと同じですが,この公式は曲線に特異点がある場合には包絡線以外の曲線をも含みます.また,包絡線の存在そのものを保障するものでもありません. |
例
次のようなパラメータ表示の関数を考えてみます.


これは楕円のパラメータ表示です.長軸と短軸の関係に注意すると,だいたい次のような曲線群が描けます.
では実際に包絡線の方程式を求めてみましょう.さきほどの公式に,これらの関数を代入します.
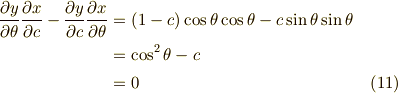
これより 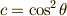 が求まりますので,これを式
が求まりますので,これを式 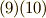 に代入すると次のようになります.
に代入すると次のようになります.


これが求める包絡線のパラメータ表示です.このままパラメータ表示にしておいてもいいのですが,たまたま 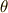 を簡単に消去できる形なのでまとめてしまいましょう.再び
を簡単に消去できる形なのでまとめてしまいましょう.再び 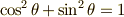 の関係を使うと次のようになります.
の関係を使うと次のようになります.
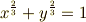
おや,これは先ほど陰関数の包絡線の例題で求めた,線分が動くときに出来る包絡線と全く同じ星芒形ですね.
このように,一見,全く異なる関数の包絡線が同じになるということが分かると,関数の大局的な振る舞いだけを知りたい時に便利なことがあるかも知れません.
補足
星芒形という図形が出てきましたが,これを円に内接するように直径四分の一の小円を転がすとき,小円の描く サイクロイド として定義することも出来ます.このように,円の内側に小円を転がして描くサイクロイドを内サイクロイド(  )と呼びます.
)と呼びます.
内サイクロイドが描かれる様子は,次のJava-appletで見ることが出来ます.動円と定円の半径比を 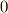 から
から 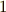 の範囲で変えられますので,色々変えて遊んでみて下さい.(半径比
の範囲で変えられますので,色々変えて遊んでみて下さい.(半径比 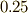 のとき,先ほどの星芒形になります.)
のとき,先ほどの星芒形になります.)
サイクロイドは最初,変分法で有名なヨハン・ベルヌーイ,ロピタルの定理で有名なロピタル公爵,微積分法で有名なライプニッツの三人によって研究されました.(この三人の人間関係については, 最速降下曲線 でより詳しく触れてあります.また,彼らのライバルであったニュートンによって伸開曲線(インボリュート)や伸閉曲線(エボリュート)が研究されました.)
ヨハン・ベルヌーイ等の研究したような古典的な問題では,なぜか包絡線として放物曲線,楕円,双曲線,サイクロイドなどがよく出てきます.
次のようなホームページでは,包絡線の描かれる様子をJavaApletで見ることが出来ます. 数学のいずみ , Eichan .
外国語で何と言うか
英語では包絡線を  と言います.日常会話で
と言います.日常会話で  と言えば封筒や包装のことです.確かに包絡線は図形をすっぽりと包む線ですが,封筒と全く同じ言葉だとは,さすが,英語は直接的です.ドイツ語では
と言えば封筒や包装のことです.確かに包絡線は図形をすっぽりと包む線ですが,封筒と全く同じ言葉だとは,さすが,英語は直接的です.ドイツ語では 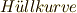 と言います.
と言います. 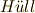 は外殻,
は外殻, 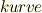 はカーブの意味ですから,さすがドイツ語は説明的です.中国語では包迹と呼ぶようです.迹という字はあまり日本では見かけませんが,軌跡というような意味ですので,やはり意味は明快です.(日本語と同じ包絡線という言葉も使うようです.そもそも,この絡という字はあまり日本では馴染みのない字ですので,日本語の包絡線が中国語から来ているという可能性があるかも知れません.由来を御存知の方は御一報下さい.)
はカーブの意味ですから,さすがドイツ語は説明的です.中国語では包迹と呼ぶようです.迹という字はあまり日本では見かけませんが,軌跡というような意味ですので,やはり意味は明快です.(日本語と同じ包絡線という言葉も使うようです.そもそも,この絡という字はあまり日本では馴染みのない字ですので,日本語の包絡線が中国語から来ているという可能性があるかも知れません.由来を御存知の方は御一報下さい.)