円錐曲線
円錐を平面で切断すると,楕円,円,放物線,二直線,双曲線となりますが, その曲線のどのような位置に焦点がくるのかを調べてみました.
円錐と平面
まず,切断したい円錐を定義します.
それは,

です.これは,直線  を
を  軸周りに回転した図形です.
軸周りに回転した図形です.
次に,切断したい平面を記述します.
それは, 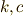 をパラメータ,
をパラメータ, 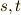 を変数として,
を変数として,

つまり,
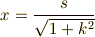

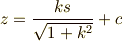
となります.
ここで, 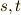 の関係がその曲線の方程式を表していると言うことを注意しておきます.
の関係がその曲線の方程式を表していると言うことを注意しておきます.
方程式の導出
式 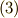 を式
を式 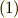 に代入します.
そこで,
に代入します.
そこで, 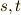 に加わる関係が断面の曲線の方程式になります.
簡単の為,
に加わる関係が断面の曲線の方程式になります.
簡単の為, 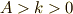 の曲線が楕円である時を考えます.
の曲線が楕円である時を考えます.

でしたから,
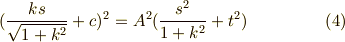
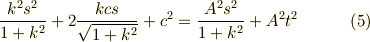
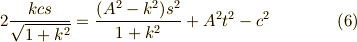
両辺を二乗して,
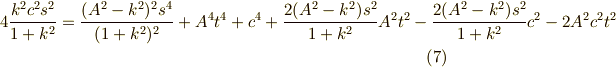
ここで, 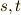 どちらの関数について,まとめるかを考えます.
この解は,
どちらの関数について,まとめるかを考えます.
この解は,  軸対称な楕円です.だから,
軸対称な楕円です.だから, 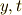 を
を  の関数と見るべきです.
つまり,
の関数と見るべきです.
つまり, 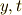 について解けば良さそうです.
ここで,
について解けば良さそうです.
ここで,

と置きます.すると,
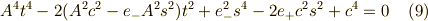
この式を良く見ると,  の四次式ですが,
の四次式ですが,  の項がないので,
の項がないので,  の二次方程式の解の公式で解けることが分かります.
の二次方程式の解の公式で解けることが分かります.
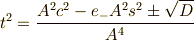
で,判別式 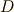 は,
は,
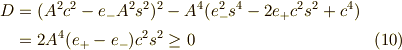
となります.よって,少し整理すると,


ここで,上の式が次のある値  を用いて表されるとします.
平方完成という手法です.
を用いて表されるとします.
平方完成という手法です.
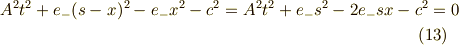
よって,
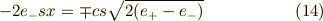

式  の左辺の後半は,
の左辺の後半は,
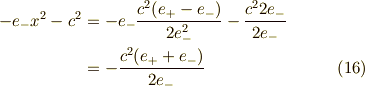
式 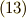 の右の等号より,
の右の等号より,
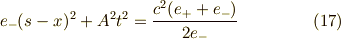
ここまで,書ければしめたものです.楕円の方程式に確かになっている事が分かりますね. さあ,右辺の数を1にしましょう.
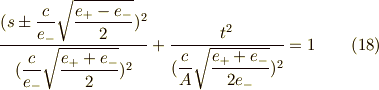
これを,

と置くと,



となります.  軸と平面が交わるところを原点とし,焦点を
軸と平面が交わるところを原点とし,焦点を 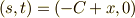 ,
, 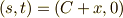 と置くと,
と置くと,

となります. 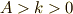 でしたので,
でしたので, 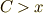 より,原点と焦点は一致しません.
ちなみに複号は,式
より,原点と焦点は一致しません.
ちなみに複号は,式 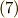 で両辺を二乗した時に
で両辺を二乗した時に  と
と 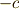 が同一視されることによるものです.
また,
が同一視されることによるものです.
また,  とすれば双曲線(
とすれば双曲線( 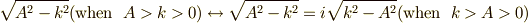 の置き換えをすればよい.)
,
の置き換えをすればよい.)
,  の極限をとれば放物線となることも分かります.特筆すべきこととして,
放物線の時は,平面と
の極限をとれば放物線となることも分かります.特筆すべきこととして,
放物線の時は,平面と  軸の交点
軸の交点 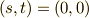 が,焦点に一致します.
が,焦点に一致します.
それでは,今日はこの辺で.