nCkはなぜ整数か
確率,場合の数でよく出てくる 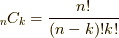 ですが,
ですが,  と
と 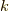 が自然数の時,
本当に,
が自然数の時,
本当に, 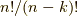 は
は 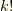 で割りきれるのでしょうか.これを示してみます.
かなり簡単に示せます.
で割りきれるのでしょうか.これを示してみます.
かなり簡単に示せます.
アプローチの方法
まず, 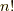 に含まれる素数
に含まれる素数 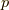 の数
の数 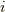 は,
ガウス記号を用いて,
は,
ガウス記号を用いて,

であることが少し考えればわかります.
これを使うと,  から並ぶ
から並ぶ 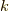 個の数の積
個の数の積 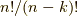 に含まれる
に含まれる 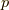 の数は,
の数は,
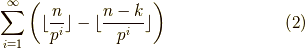
となります.そして, 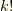 に含まれる
に含まれる 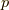 の数は,
の数は,

ここで, 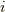 を任意に取った時,
を任意に取った時,
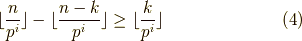
を示せれば,OKです.
不等式の評価
式 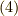 は簡単に示せます.
一般に実数
は簡単に示せます.
一般に実数  に対して,
に対して,

が言えるので,
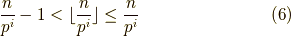
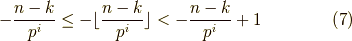
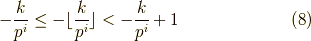
式 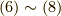 を辺々足して,
を辺々足して,
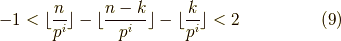
よって,式  の値は整数なので,
の値は整数なので, 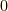 か
か 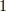 になるので,
式
になるので,
式 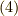 が成立することになります.これで,
が成立することになります.これで, 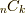 が整数になることが示せました.
が整数になることが示せました.
さらに言えば,式 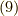 の中辺を
の中辺を 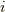 で和をとった値
で和をとった値 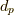 ,
,
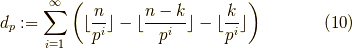
は, 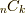 は
は 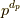 で割れることを示しています.
今日はここまで,お疲れ様でした.
で割れることを示しています.
今日はここまで,お疲れ様でした.