行列の階数を区別するものは何か?
みなさんは, 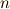 次行列
次行列 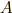 の
の 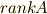 に
ついて,
に
ついて,  の時,正則なのはわかった,
じゃあ,
の時,正則なのはわかった,
じゃあ, 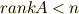 の時は,どんな性質を持っているのだろう.
特に
の時は,どんな性質を持っているのだろう.
特に  の時,
の時, 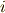 と
と  の違いは?
と考えたことはありませんか?
その疑問の一つに答えるのが,この記事です.
数学になれている方は,「具体例」を飛ばして,「定理」まで飛んでしまって構いません.
の違いは?
と考えたことはありませんか?
その疑問の一つに答えるのが,この記事です.
数学になれている方は,「具体例」を飛ばして,「定理」まで飛んでしまって構いません.
具体例
まずは,次の二次正方行列(  )の違いを調べてみましょう.
)の違いを調べてみましょう.
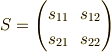
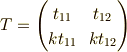
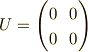
ここで, 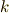 はある
はある 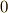 でない実数です.
これらの行列は,上から順に
でない実数です.
これらの行列は,上から順に 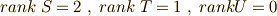 です.
この内,
です.
この内, 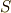 は,
は,  として区別がつきます.
では,
として区別がつきます.
では, 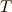 と
と 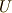 は,どうやって区別したらいいのでしょうか?
は,どうやって区別したらいいのでしょうか?
僕は,試しに固有方程式を思い出して,  と
と  (ただし,
(ただし,  は
ある数,
は
ある数, 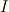 は単位行列)を作ってみることにしました.
は単位行列)を作ってみることにしました.
すると,
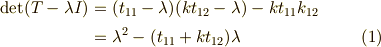

なんらかの対称性により,  の方では,
の方では,  のゼロ乗の係数を
のゼロ乗の係数を  に,
に, 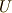 では,
では,  の一乗とゼロ乗の係数を
の一乗とゼロ乗の係数を 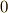 になったと考えられるのではないでしょうか?
になったと考えられるのではないでしょうか?
次に同様に三次の行列( 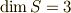 )を考えてみます.
)を考えてみます.
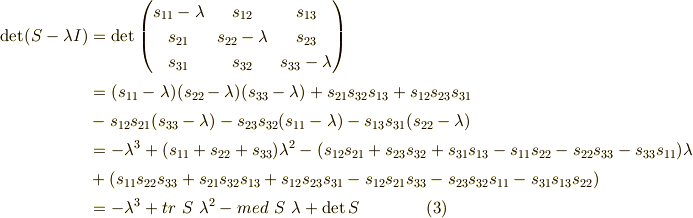
式 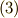 で,
で,  と定義しました.(
と定義しました.(  は,「中間」
は,「中間」  から名づけました.)
から名づけました.)
ここで,  の場合の一例を考えてみましょう.例えば,
の場合の一例を考えてみましょう.例えば,

ここで, 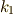 と
と  は,ある定数です.この時,
は,ある定数です.この時,
三次の係数: 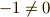 ,
,
二次の係数: 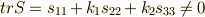
一次の係数: 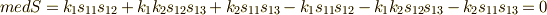
0次の係数: 
またまた,なんらかの対称性により,一次とゼロ次の係数はゼロに なりました.
次は,  の時を考えます.
の時を考えます.
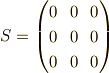
この時,三次の係数以外は,すべてゼロになります.
まとめると, 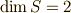 の時,
の時, 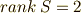 なら係数がゼロにならない,
なら係数がゼロにならない,  の時,ゼロ次の係数がゼロ,
の時,ゼロ次の係数がゼロ, 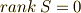 なら,一次の
係数までゼロ.
なら,一次の
係数までゼロ. 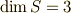 の時,
の時,  の時,
の時, 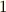 次までゼロ,
次までゼロ, 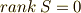 の時,
の時,  次までゼロ.
ここから予想できるのは,次のような法則です.
次までゼロ.
ここから予想できるのは,次のような法則です.
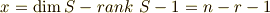
と置くと,  次の項まで,ゼロになるのでしょう.
次の項まで,ゼロになるのでしょう.
実際それは正しく,なりたちます. 詳しくは,次の証明を見てください.
定理
theorem
n次の正方行列 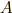 で,
で, 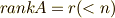 のとき,特性多項式
のとき,特性多項式 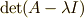 は,
は, 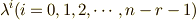 の係数が
の係数が 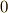 となる.
となる.
(証明)
右基本変形 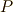 ,左基本変形
,左基本変形  によって(この時,
によって(この時, 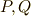 は
は 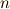 次正則行列),任意の
次正則行列),任意の 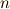 次正方行列
次正方行列 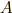 は,
次の標準形
は,
次の標準形 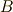 (n次正方行列)に変形することができる.
(n次正方行列)に変形することができる.
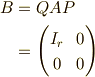
ただし, 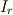 は
は  次の単位行列とする.
次の単位行列とする.
ここで, 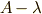 の特性多項式
の特性多項式  を考え,
行列式を取る記号を
を考え,
行列式を取る記号を 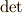 でなく,
でなく,  で表すと,
で表すと,

ここで, 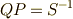 と置くと,
と置くと, 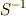 は正則行列なので,逆行列
は正則行列なので,逆行列 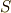 を持ちますので,
を持ちますので,

よって, 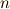 次多項式である,
次多項式である, 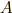 の
特性多項式は,
の
特性多項式は,  の
の 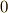 次から,
次から, 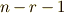 次の項 [*] までの係数は,ゼロとなります.
次の項 [*] までの係数は,ゼロとなります.
| [*] | : ここで 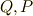 は正則なので, は正則なので, 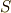 は正則.しかし, は正則.しかし, 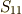 も正則で も正則で 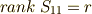 となるとは限らず,正確には,「少なくとも となるとは限らず,正確には,「少なくとも 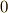 次から 次から 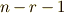 次までは,係数がゼロ.」「しかし,n-r次以上の係数もゼロかも知れない」となります. 次までは,係数がゼロ.」「しかし,n-r次以上の係数もゼロかも知れない」となります. |
長年の疑問が晴れてすっきりしました(安堵).