三重対角行列の特性多項式
三重対角行列の特性多項式を求める漸化式を 求めてみます.
まず,三重対角行列 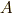 を書きます.
を書きます.
単位行列を 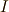 として,この行列の特性多項式を求めます.
つまり,
として,この行列の特性多項式を求めます.
つまり, 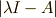 を求めます.
縦線での括弧は,行列式を表します.
を求めます.
縦線での括弧は,行列式を表します. 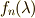 を次のように定義します.
を次のように定義します.
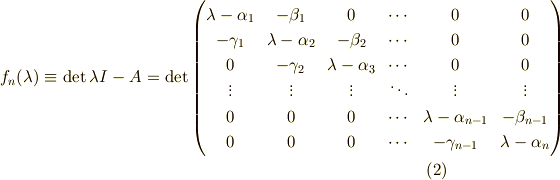
すると,一番下の行(横ベクトル)のラプラス展開によって,次のような漸化式が得られます.
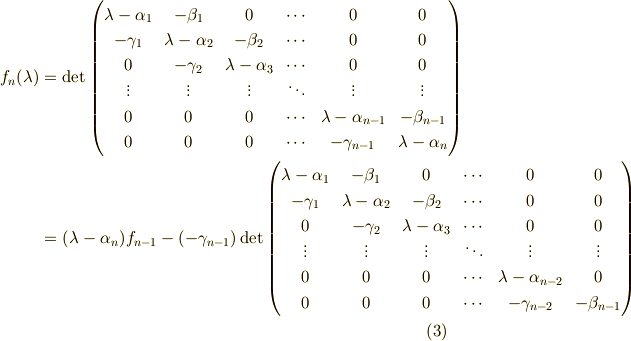
ここで,最後の式で第二項は,最後の列(縦ベクトル)で展開すると, 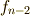 と
と 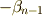 の積で表現できまして,
の積で表現できまして,
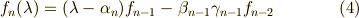
こうして,うまく漸化式が立てられました.
実際に計算してみると, 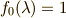 とすれば,
うまく計算のつじつまが合いまして,
とすれば,
うまく計算のつじつまが合いまして,


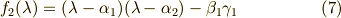
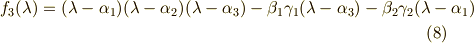
と,この様に次々特性多項式が求まっていきます. それでは,今日はこの辺で.